[题解]CodeForces878C Tournament

传送门

想了好久都没有想出来，幼小

题目描述

(n)个人参加一个有(k)项活动的比赛，第(i)个人完成第(j)项活动的能力为(a[i][j])

每一次选两个人，随机指定一项活动，能力强的人胜出并留下，另一人淘汰，最后留下的人获胜

问对于每一个(ileq n)，前(i)个人中有几个人可能获胜

((1leq n leq 5*10^4,1leq k leq 10,1leq a[i][j]leq 10^9),保证(a)互不相同)

分析

把人看成点，对于(u,v)，如果(u)可以打败(v)，从(u)向(v)连边。

显然，一个人可以赢当且仅当可以以它为根拎出一棵有向树。

考虑怎么维护：

可以发现，环上的每一个点的地位是相同的，所以可以先把环缩掉，然后把剩下的联通块扯成一条链，再把其他边删掉——像这样。(u)可以到达(v)当且仅当(u)可以打败(v)

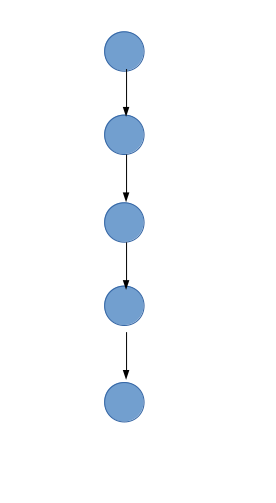
那么我们要求的，就是入度为0的联通块的大小

而且，我们发现这些联通块有一个有趣的性质就是，按照拓扑序，每一项活动的最大能力值和最小能力值都是单调的。即，记(mx/mn[x][i])为(x)所在的联通块里，所有点中第(i)项活动的最大/小能力值，那么对于(u)可以走到(v),(forall i,mn[u][i]>mn[v][i],mx[u][i]>mx[v][i])

那么我们就可以用set维护每一个联通块。

再考虑加入新的点，可能会产生新的环，像下面的图一样 。那么我们只需要通过lower_bound找到粉红色的点(第一个可以打败新增点的点)，然后一直往后走合并就可以啦

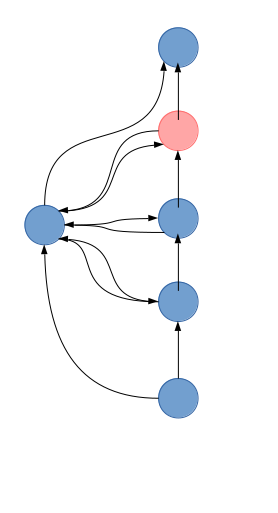
代码

好像并不是特别长，然而写了好久。

set真骚气神奇啊，还有lower_bound

#include<bits/stdc++.h>
#define rep(X,A,B) for(int X=A;X<=B;X++)
#define tep(X,A,B) for(int X=A;X>=B;X--)
#define LL long long
const int N=50010;
using namespace std;

int n,m;
//---
struct nn{
	int mn[11],mx[11],sz,pd;
};

nn g[N];
//---
int WIN(nn A,nn B){
	rep(i,1,m)if(A.mx[i]>B.mn[i])return 1;
	return 0;
}
//
struct node{
	int val;
	
	bool operator <(const node &A)const {
		int x=val,y=A.val;
		if(g[y].pd==0)return !WIN(g[x],g[y]);
		return WIN(g[y],g[x]);
	}
};

set<node>mp;
set<node>::iterator pos,del;
//---
nn MERGE(nn A,nn B){
	nn res;
	res.pd=A.pd;
	res.sz=A.sz+B.sz;
	rep(i,1,m){
		res.mn[i]=min(A.mn[i],B.mn[i]);
		res.mx[i]=max(A.mx[i],B.mx[i]);
	}
	return res;
}

void SOLVE(int id){
	int x;
	g[id].sz=1;g[id].pd=0;
	rep(i,1,m){
		scanf("%d",&x);
		g[id].mn[i]=g[id].mx[i]=x;
	}
	pos=mp.lower_bound((node){id});
	while(pos!=mp.end()){
		int now=(*pos).val;
		if(WIN(g[id],g[now])&&WIN(g[now],g[id])){
			g[id]=MERGE(g[id],g[now]);
			del=pos;pos++;
			mp.erase(del);
		}
		else break;
	}
	g[id].pd=1;
	mp.insert((node){id});
	int now=(*mp.rbegin()).val;
	printf("%d
",g[now].sz);
}

int main(){
	scanf("%d%d",&n,&m);
	rep(i,1,n)SOLVE(i);
	return 0;
}