(\)
Description
求 (N imes M) 的网格图上有多少个格点构成的三角形。
当三点共线的时候我们不认为这是一个三角形。
- (n,mle 10^4)
(\)
Solution
正难则反。容斥出答案。
总的选择三个点的方案数为 (C_{n imes m}^3) 。
需要去掉:
-
同一行的三个点 (n imes C_m^3)
-
同一列的三个点 (m imes C_n^3)
-
共斜线上的三个点。
但是注意!斜线的斜率可能不为 (1) 或 (-1) 。
因为有这样的东西存在:
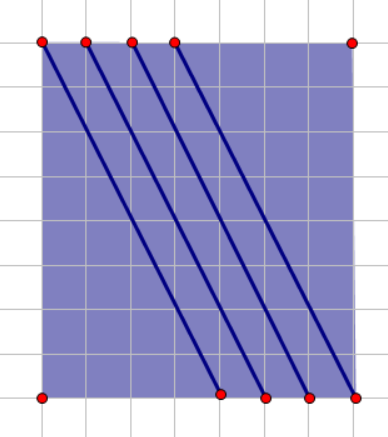
考虑怎么去掉每一条斜线上选三个整点的方案数。
这个思路就很厉害了。
考虑枚举一个向量。
对于枚举的一个向量 ((i,j) | ile n,jle m) ,在整个网格图中有((n-i) imes(m-j) imes 2) 个线段与之对应。
解释一下 ( imes 2) 的含义是,对斜率取相反数得到的所有线段,显然个数与原来相同。
然后为了不重复,我们强制选择线段的两个端点,然后选择一个线段上的整点。
线段上不算端点的整点个数是 ((i,j)-1) ,因为这一线段上整点坐标只能表示为 ((frac i{(i,j)} imes k,frac j{(i,j)} imes k))
然后在总方案里去掉 (C_{(i,j)-1}^1 imes (n-i) imes (m-j) imes 2) 就可以了。
关于正确性多说一句:
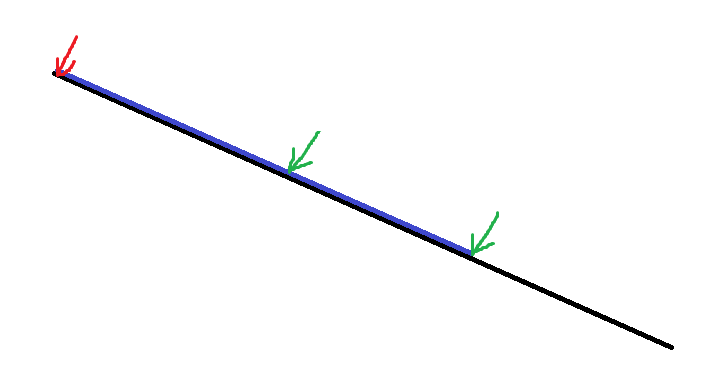
考虑两个重合的向量,大的向量计数里一定不会包含小的计数,因为小的计数的每一个情况,都有两个点在大的线段上,不符合大的计数要求。
如图,蓝线上一个合法的组合用三个箭头表示,其中必然存在形如绿色的两个箭头的选择,而他们都在黑色线段上,不符合黑色计数要求。
(\)
Code
#include<cmath>
#include<cstdio>
#include<cctype>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define R register
using namespace std;
typedef long long ll;
ll n,m,ans;
ll C(ll x){return (x*(x-1)/2)*(x-2)/3;}
ll gcd(ll a,ll b){return b?gcd(b,a%b):a;}
int main(){
scanf("%lld%lld",&n,&m);
++n; ++m;
ans=C(n*m)-n*C(m)-m*C(n);
for(R ll i=1;i<=n;++i)
for(R ll j=1,res;j<=m;++j){
res=1+gcd(i,j);
if(res>=3) ans-=(res-2)*(n-i)*(m-j)*2;
}
printf("%lld
",ans);
return 0;
}