图的定义
G=(V,E)
G代表图
V代表|V|为结点数
E代表|E|为边的条数
图的表示
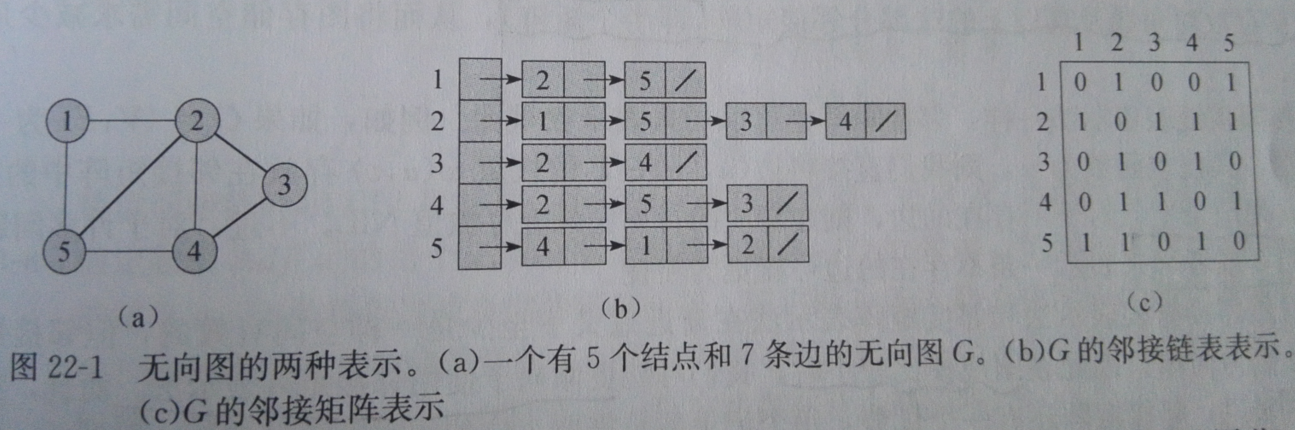
图的常规标准表示方式有两种,一种是邻接链表、一种是邻接矩阵。
在稀疏图中多用链表,稠密图中多用矩阵。(稀疏与稠密看的是|E|与|V|的2次方的比较,|E|远远小于|V|的2次方为稀疏图)
邻接链表的一大缺点是无法快速判断一条边是否是图中的,唯一的办法是搜索结点找边。
图规模比较小时,更倾向于使用邻接矩阵表示法。
广度优先搜索
Prim的最小生成树算法和Dijkstra的单源最短路径算法都用了广度优先搜索。
深度优先搜索
最小生成树
无向图中的最小权重树为最小生成树
定义:在连通无向图G=(V,E)中找到一个无环子集T属于E,既能够将所有的结点(针脚)连接起来,又具有最小的权重。由于T是无环的,并且连通所有结点,因此,T必然是一棵树。我们称之为最小生成树。
Kruskal算法和Prim算法
这两个算法都是最小生成树算法
Kruskal算法
每次找最小的边,看是否在同一个树里(边(u,v)中u和v都在树里则为不安全)
用的贪心策略
下面为伪代码和解释
MST-KRUSKAL(G,w) A=null for each vertex v∈G.V MAKE-SET(v) //初始化树根 sort the edges of G.E into nondecreasing order by weight w for each edge(u,v)∈G.E, take in nondecreasing order by weight //循环边(最小权到最大权) if FIND-SET(u) != FIND-SET(v) //u与v是否同一棵树 A=AU{(u,v)} //A中加入边(u,v) UNION(u,v) //两棵树中的结点合并 return A
Prim算法
从一个点开始贪心其中最小的权边加入树中
下面为伪代码
MST-PRIM(G,w,r) for each u∈G.V //初始化每个结点u属于G.V u:key = 无限 //u.key=无穷 u:π = NIL //u.π=空 r:key = 0; //根点的最小权为0 Q=G.V //最小优先队列初始化为G.V while Q != null u=EXTRACT-MIN(Q) //找Q中最小权点赋值给u for each v∈G.Adj[u] //循环与u相连的点v if v∈Q and w(u,v) < v.key //如果v属于Q 点u的权值加上边(u,v)的权值小于v.key v.π = u //v点的父结点 = u v.key = w(u,v) //v点的权值 = 点u的权值加上边(u,v)的权值
单源最短路径
定义:给定一个图G=(V,E),我们希望找到从给定源结点s∈V到每个结点v∈V的最短路径。
几个变体问题:
1)单目的地最短路径问题:每个结点v到给定目的地点的最短路径
2)单结点对最短路径问题:结点u到结点v的最短路径
3)所有结点对最短路径问题:对于每个结点u和v,找到其最短路径
最短路径的最优子结构
两个结点之间的一条最短路径包含着其他的最短路径(最短路径的子路径也是最短路径)。
最短路径的表示
用前驱子图的表示方法,具体形式为每个结点开辟一个空间存储它的上一结点。(其实另开辟一个数组也是可以的)
松弛操作
松弛技术:对于每个结点v来说,我们维持一个属性v.d,用来记录从源结点s到结点v的最短路径权重的上界。我们称v.d为s到v的最短路径估计。
松弛过程:v结点本身有一个最短估计值为v.d,又找到一条到v的路径把权值跟v.d进行比较,如果后者小,则更新v.d和v.π。
以下是伪代码
PELAX(u,v,w) if v.d > u.d + w(u,v) //如果新路径权值小于原来的估算权值 v.d = u.d + w(u,v) //估算权值被更新 v.π = u //前驱更新
Bellman-Ford算法
注意:此算法可处理边权值为负值的情况,此算法可判断出负值成环的存在。
以下为伪代码
BELLMAN-FORD(G,w,s) INITIALIZE-SINGLE-SOURCE(G,s) //初始化图 for i = 1 to |G.V| - 1 //循环全部结点 for each edge(u,v)∈G.E //循环每个结点所连边 RELAX(u,v,w) //松弛操作 for each edge(u,v)∈G.E //循环每条边 if v.d > u.d + w(u,v) //测试是否还能松弛,从而找到环 return FALSE //如果能松弛,则返回False return TRUE //运行正确放回True
有向无环图的单源最短路径问题
根据结点的拓扑排序次序来对带权重的有向无环图G=(V,E)进行边的松弛。
注意:1.如果源结点s不是拓扑排序后的第一个结点,直到找到源结点s前的所有结点可以无视。
2.边权非负
以下是伪代码
DAG-SHORTEST-PATHS(G,w,s) topologically sort the vertices of G //拓扑排序图G INITALIZE-SINGLE-SOURCE(G,s) //初始化G,并设源点s for each vertex u, taken in topologically sorted order //按拓扑排序后结点顺序循环结点 for each vertex v∈G.Adj[u] //循环结点所连边 RELAX(u,v,w) //松弛操作
Dijkstra算法
解决带权重的有向图上单源最短路径问题
注意:1.边权非负
2.Dijkstra算法比Bellman-Ford算法运行速度快。
算法核心思想:重复从结点集V-S中选择最短路径估计最小的结点u,加入集合S,对从u出发的边进行松弛。(V为全部结点集合,S为已使用结点集合)
以下是伪代码
DIJKSTRA(G,w,s) INITIALIZE-SINGLE-SOURCE(G,s) //初始化图G,设源点s S=空 //初始化集合S为空 Q=G.V //初始化集合Q,为V while Q != 空 u = EXTRACT-MIN(Q) //找出Q中最小估算结点,赋值给u,并在Q中删除 S = S U {u} //将结点u加入集合S中 for each vertex v∈G.Adj[u] //循环与u相连的每个点 RELAX(u,v,w) //松弛操作