AC 自动机

概述

AC 自动机是 以 Trie 的结构为基础 ，结合 KMP 的思想 建立的。

简单来说，建立一个 AC 自动机有两个步骤：

1. 基础的 Trie 结构：将所有的模式串构成一棵 Trie。
2. KMP 的思想：对 Trie 树上所有的结点构造失配指针。

然后就可以利用它进行多模式匹配了。

字典树构建

AC 自动机在初始时会将若干个模式串丢到一个 Trie 里，然后在 Trie 上建立 AC 自动机。这个 Trie 就是普通的 Trie，该怎么建怎么建。

这里需要仔细解释一下 Trie 的结点的含义，尽管这很小儿科，但在之后的理解中极其重要。Trie 中的结点表示的是某个模式串的前缀。我们在后文也将其称作状态。一个结点表示一个状态，Trie 的边就是状态的转移。

形式化地说，对于若干个模式串 (s_1,s_2dots s_n) ，将它们构建一棵字典树后的所有状态的集合记作 (Q) 。

失配指针

AC 自动机利用一个 fail 指针来辅助多模式串的匹配。

状态 (u) 的 fail 指针指向另一个状态 (v) ，其中 (vin Q) ，且 (v) 是 (u) 的最长后缀（即在若干个后缀状态中取最长的一个作为 fail 指针）。对于学过 KMP 的朋友，我在这里简单对比一下这里的 fail 指针与 KMP 中的 next 指针：

1. 共同点：两者同样是在失配的时候用于跳转的指针。
2. 不同点：next 指针求的是最长 Border（即最长的相同前后缀），而 fail 指针指向所有模式串的前缀中匹配当前状态的最长后缀。

因为 KMP 只对一个模式串做匹配，而 AC 自动机要对多个模式串做匹配。有可能 fail 指针指向的结点对应着另一个模式串，两者前缀不同。

没看懂上面的对比不要急（也许我的脑回路和泥萌不一样是吧），你只需要知道，AC 自动机的失配指针指向当前状态的最长后缀状态即可。

AC 自动机在做匹配时，同一位上可匹配多个模式串。

构建指针

下面介绍构建 fail 指针的 基础思想 ：（强调！基础思想！基础！）

构建 fail 指针，可以参考 KMP 中构造 Next 指针的思想。

考虑字典树中当前的结点 (u) ， (u) 的父结点是 (p) ， (p) 通过字符 c 的边指向 (u) ，即 (trie[p,c]=u) 。假设深度小于 (u) 的所有结点的 fail 指针都已求得。

1. 如果 ( ext{trie}[ ext{fail}[p],c]) 存在：则让 u 的 fail 指针指向 ( ext{trie}[ ext{fail}[p],c]) 。相当于在 (p) 和 ( ext{fail}[p]) 后面加一个字符 c ，分别对应 (u) 和 (fail[u]) 。
2. 如果 ( ext{trie}[ ext{fail}[p],c]) 不存在：那么我们继续找到 ( ext{trie}[ ext{fail}[ ext{fail}[p]],c]) 。重复 1 的判断过程，一直跳 fail 指针直到根结点。
3. 如果真的没有，就让 fail 指针指向根结点。

如此即完成了 ( ext{fail}[u]) 的构建。

例子

下面放一张 GIF 帮助大家理解。对字符串 i he his she hers 组成的字典树构建 fail 指针：

1. 黄色结点：当前的结点 (u) 。
2. 绿色结点：表示已经 BFS 遍历完毕的结点，
3. 橙色的边：fail 指针。
4. 红色的边：当前求出的 fail 指针。

我们重点分析结点 6 的 fail 指针构建：

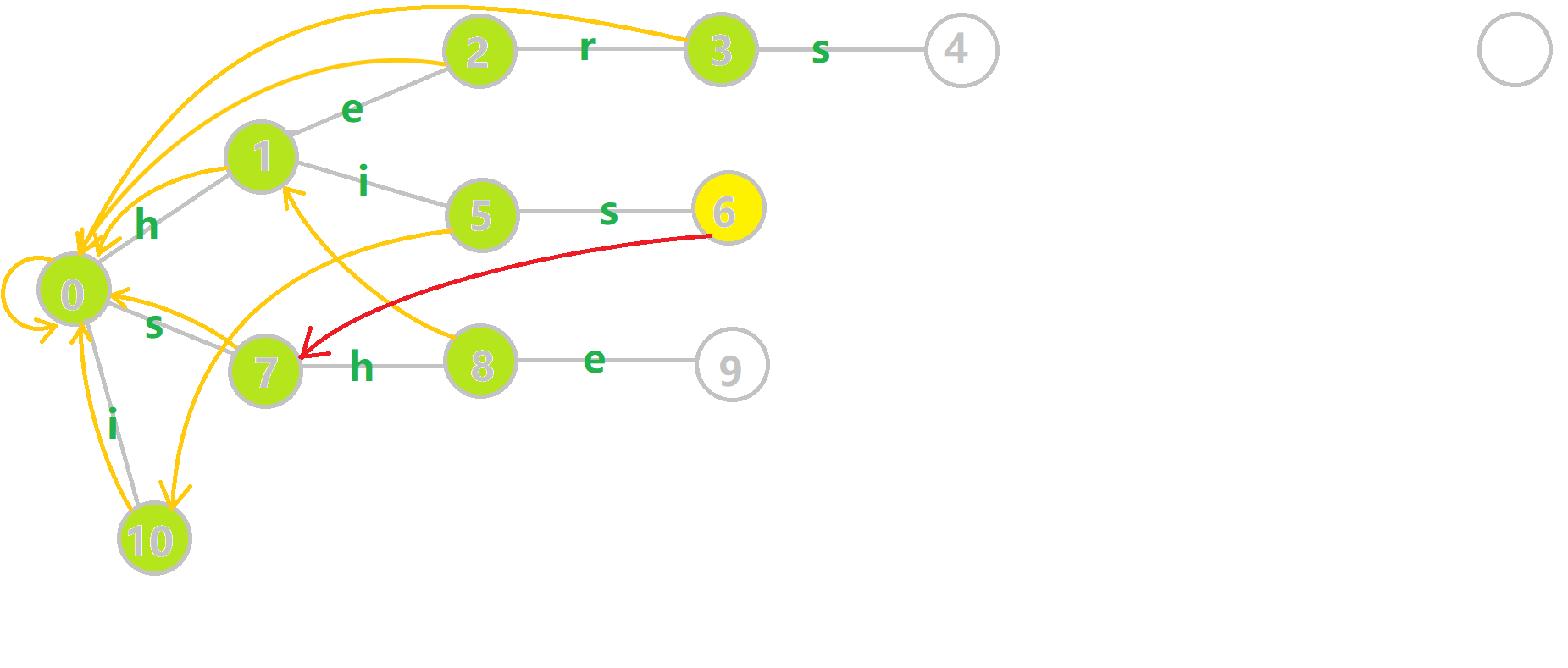
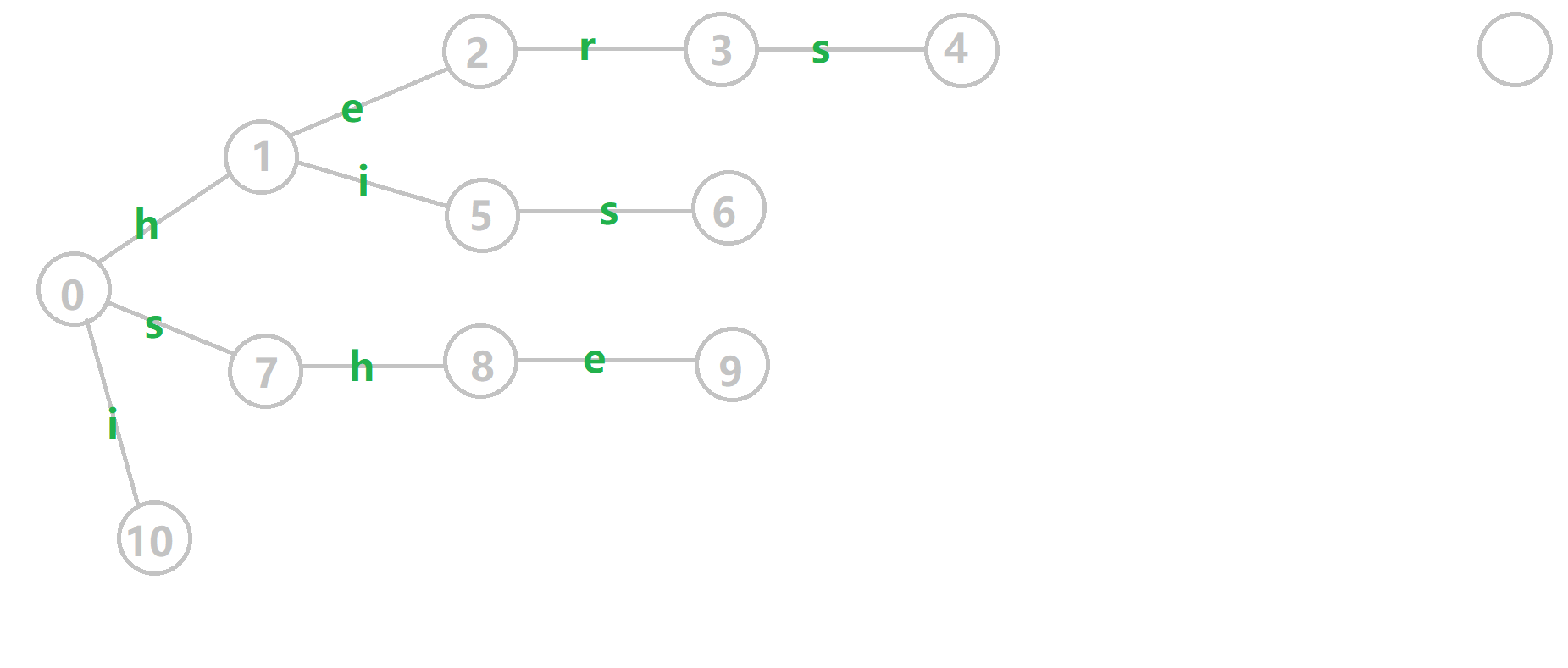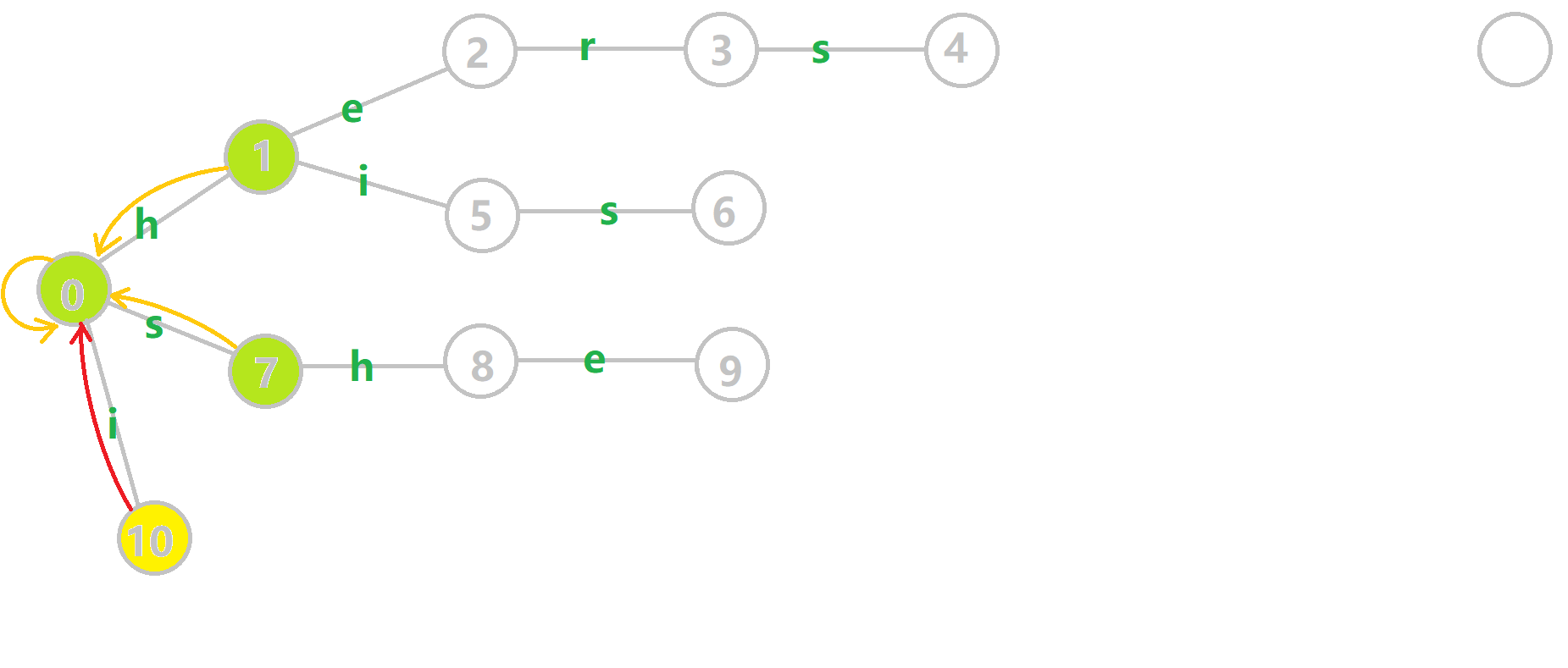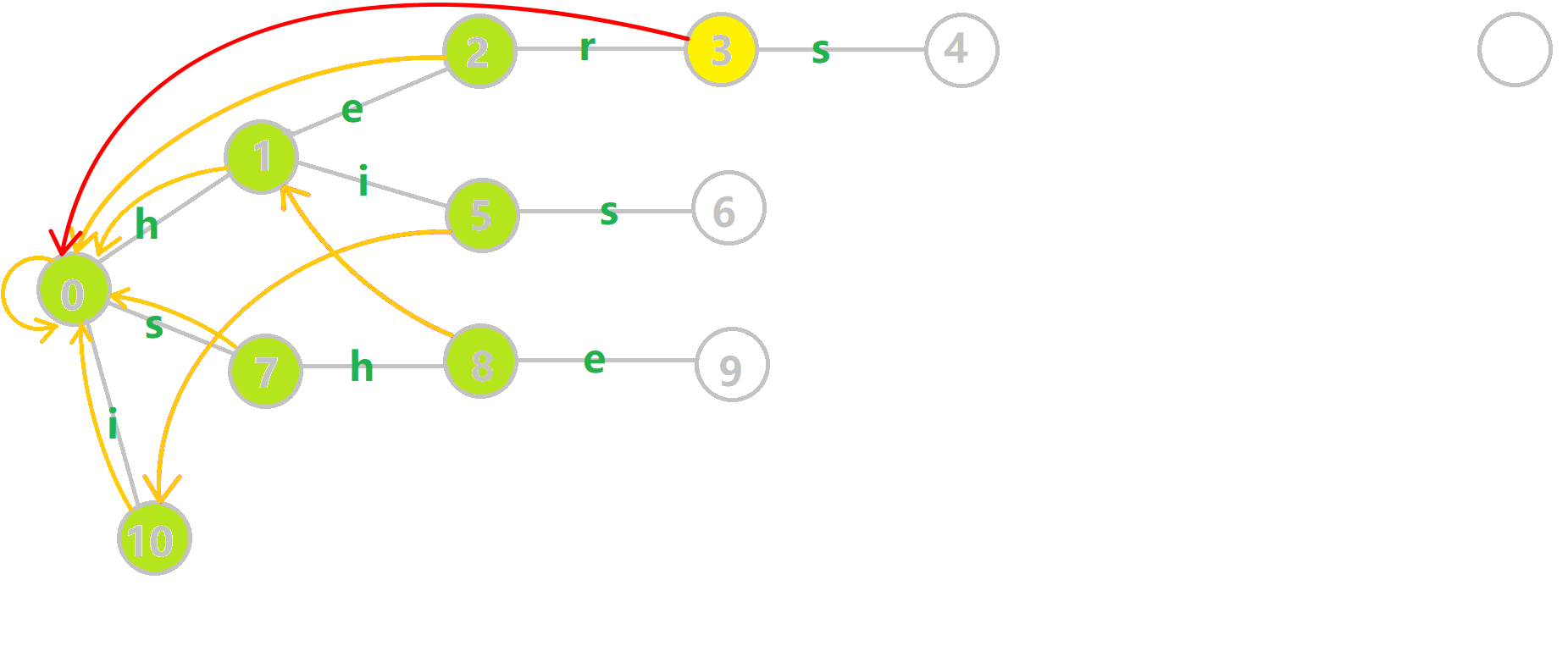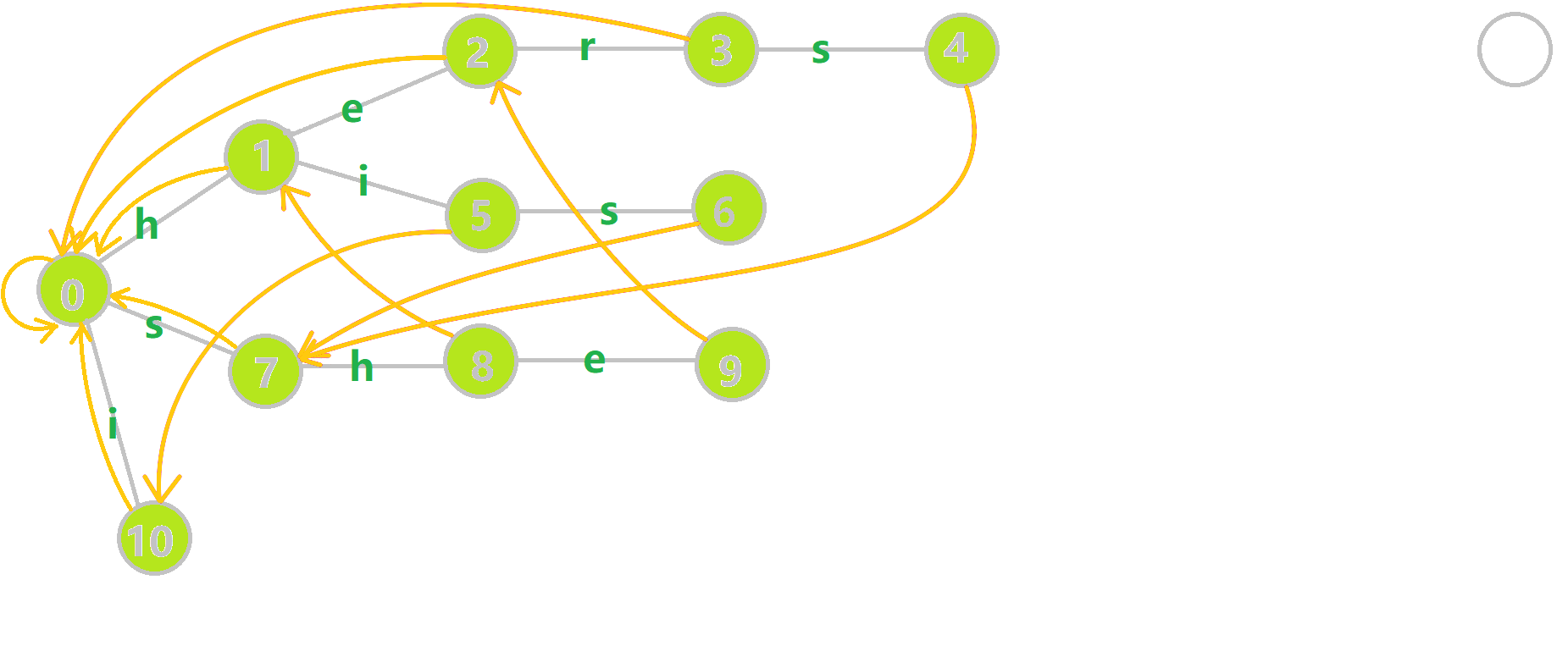
找到 6 的父结点 5， ( ext{fail}[5]=10) 。然而 10 结点没有字母 s 连出的边；继续跳到 10 的 fail 指针， ( ext{fail}[10]=0) 。发现 0 结点有字母 s 连出的边，指向 7 结点；所以 ( ext{fail}[6]=7) 。最后放一张建出来的图

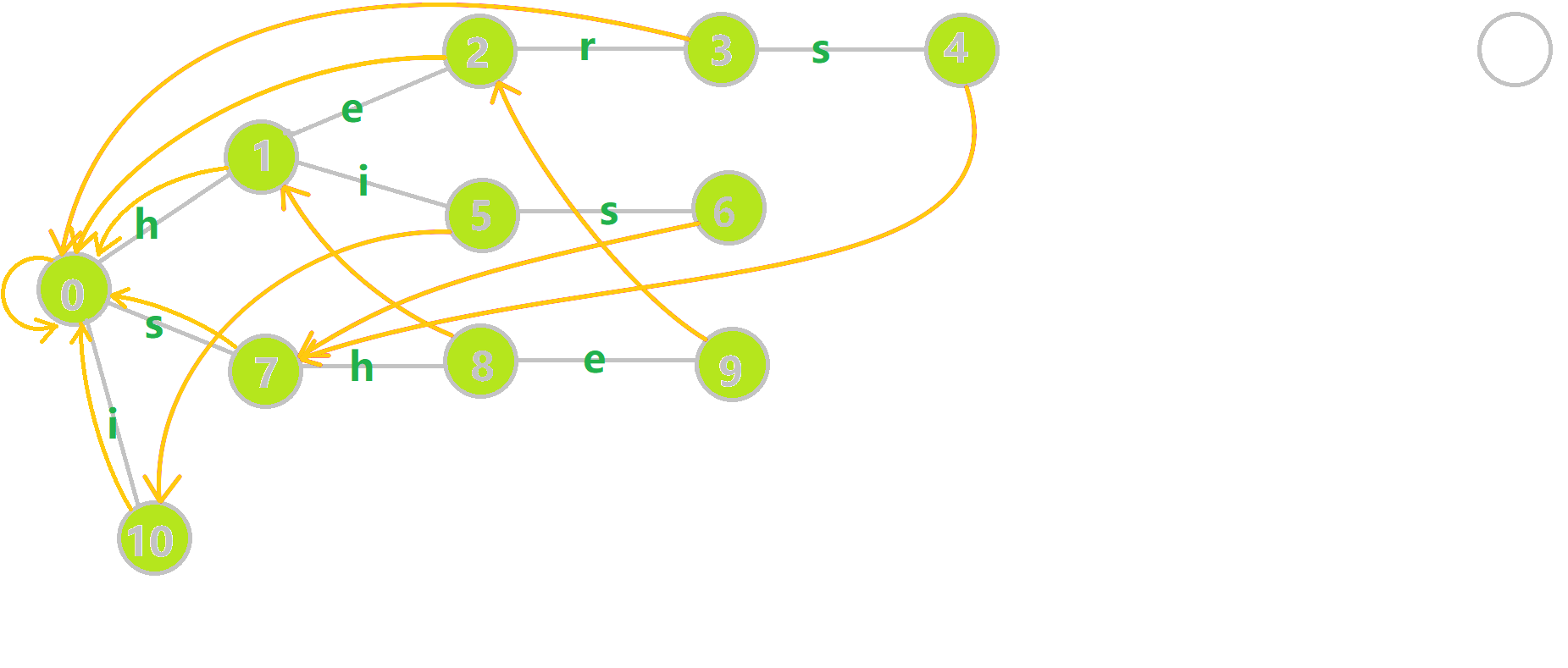
字典树与字典图

我们直接上代码吧。字典树插入的代码就不分析了（后面完整代码里有），先来看构建函数 build() ，该函数的目标有两个，一个是构建 fail 指针，一个是构建自动机。参数如下：

1. tr[u,c] ：有两种理解方式。我们可以简单理解为字典树上的一条边，即 ( ext{trie}[u,c]) ；也可以理解为从状态（结点） (u) 后加一个字符 c 到达的状态（结点），即一个状态转移函数 ( ext{trans}(u,c)) 。下文中我们将用第二种理解方式继续讲解。
2. 队列 q ：用于 BFS 遍历字典树。
3. fail[u] ：结点 (u) 的 fail 指针。

void build() {
  for (int i = 0; i < 26; i++)
    if (tr[0][i]) q.push(tr[0][i]);
  while (q.size()) {
    int u = q.front();
    q.pop();
    for (int i = 0; i < 26; i++) {
      if (tr[u][i])
        fail[tr[u][i]] = tr[fail[u]][i], q.push(tr[u][i]);
      else
        tr[u][i] = tr[fail[u]][i];
    }
  }
}

解释一下上面的代码：build 函数将结点按 BFS 顺序入队，依次求 fail 指针。这里的字典树根结点为 0，我们将根结点的子结点一一入队。若将根结点入队，则在第一次 BFS 的时候，会将根结点儿子的 fail 指针标记为本身。因此我们将根结点的儿子一一入队，而不是将根结点入队。

然后开始 BFS：每次取出队首的结点 u（ ( ext{fail}[u]) 在之前的 BFS 过程中已求得），然后遍历字符集（这里是 0-25，对应 a-z，即 (u) 的各个子节点）：

1. 如果 ( ext{trans}[u][i]) 存在，我们就将 ( ext{trans}[u][i]) 的 fail 指针赋值为 ( ext{trans}[ ext{fail}[u]][i]) 。这里似乎有一个问题。根据之前的讲解，我们应该用 while 循环，不停的跳 fail 指针，判断是否存在字符 i 对应的结点，然后赋值，但是这里通过特殊处理简化了这些代码。
2. 否则，令 ( ext{trans}[u][i]) 指向 ( ext{trans}[ ext{fail}[u]][i]) 的状态。

这里的处理是，通过 else 语句的代码修改字典树的结构。没错，它将不存在的字典树的状态链接到了失配指针的对应状态。在原字典树中，每一个结点代表一个字符串 (S) ，是某个模式串的前缀。而在修改字典树结构后，尽管增加了许多转移关系，但结点（状态）所代表的字符串是不变的。

而 ( ext{trans}[S][c]) 相当于是在 (S) 后添加一个字符 c 变成另一个状态 (S') 。如果 (S') 存在，说明存在一个模式串的前缀是 (S') ，否则我们让 ( ext{trans}[S][c]) 指向 ( ext{trans}[ ext{fail}[S]][c]) 。由于 ( ext{fail}[S]) 对应的字符串是 (S) 的后缀，因此 ( ext{trans}[ ext{fail}[S]][c]) 对应的字符串也是 (S') 的后缀。

换言之在 Trie 上跳转的时侯，我们只会从 (S) 跳转到 (S') ，相当于匹配了一个 (S') ；但在 AC 自动机上跳转的时侯，我们会从 (S) 跳转到 (S') 的后缀，也就是说我们匹配一个字符 c ，然后舍弃 (S) 的部分前缀。舍弃前缀显然是能匹配的。那么 fail 指针呢？它也是在舍弃前缀啊！试想一下，如果文本串能匹配 (S) ，显然它也能匹配 (S) 的后缀。所谓的 fail 指针其实就是 (S) 的一个后缀集合。

tr 数组还有另一种比较简单的理解方式：如果在位置 (u) 失配，我们会跳转到 ( ext{fail}[u]) 的位置。所以我们可能沿着 fail 数组跳转多次才能来到下一个能匹配的位置。所以我们可以用 tr 数组直接记录记录下一个能匹配的位置，这样就能节省下很多时间。

这样修改字典树的结构，使得匹配转移更加完善。同时它将 fail 指针跳转的路径做了压缩（就像并查集的路径压缩），使得本来需要跳很多次 fail 指针变成跳一次。

好的，我知道大家都受不了长篇叙述。上图！我们将之前的 GIF 图改一下：

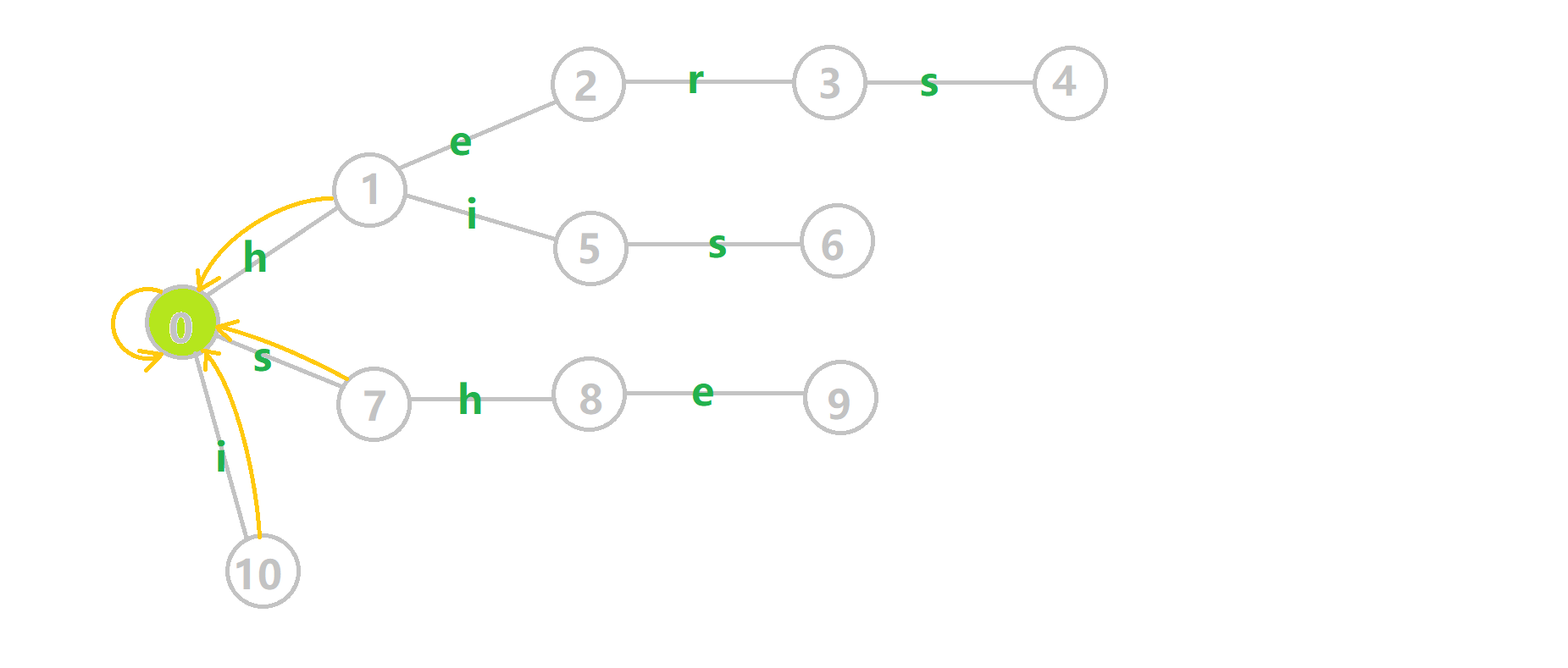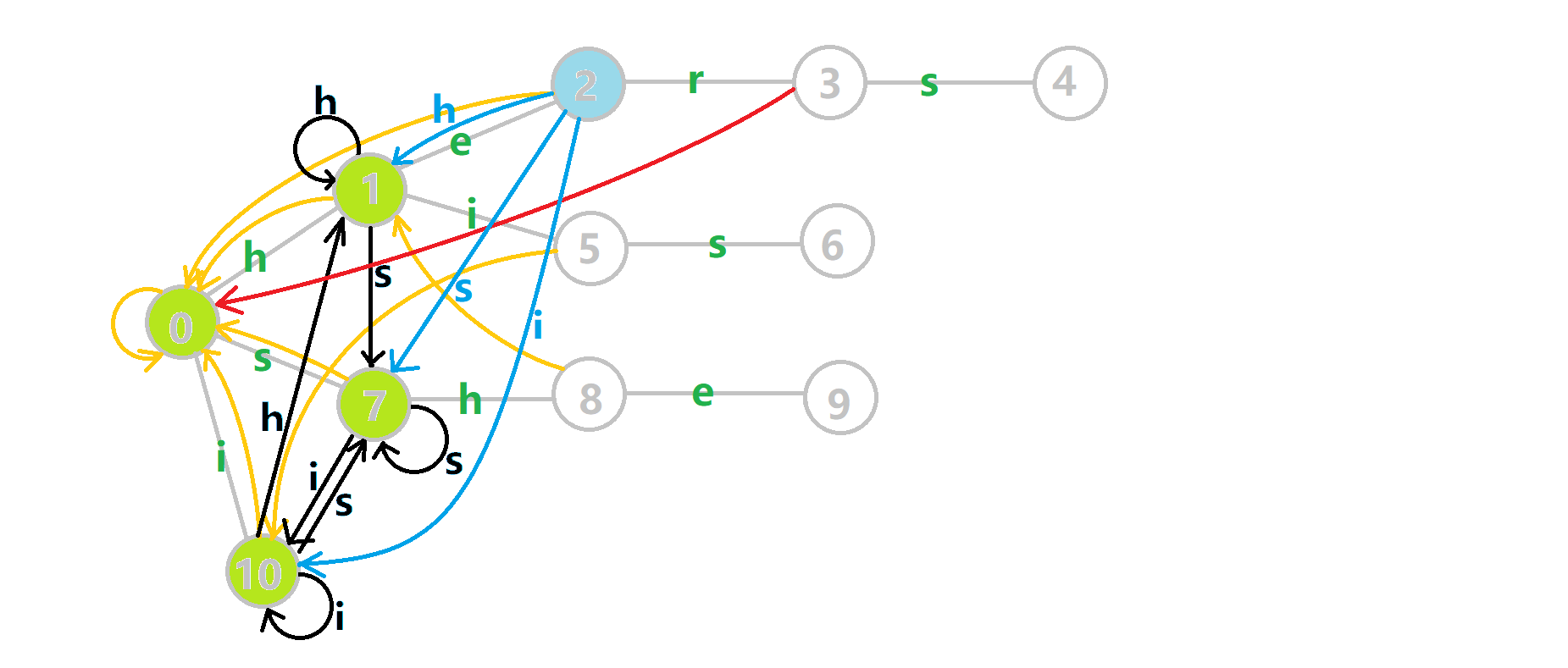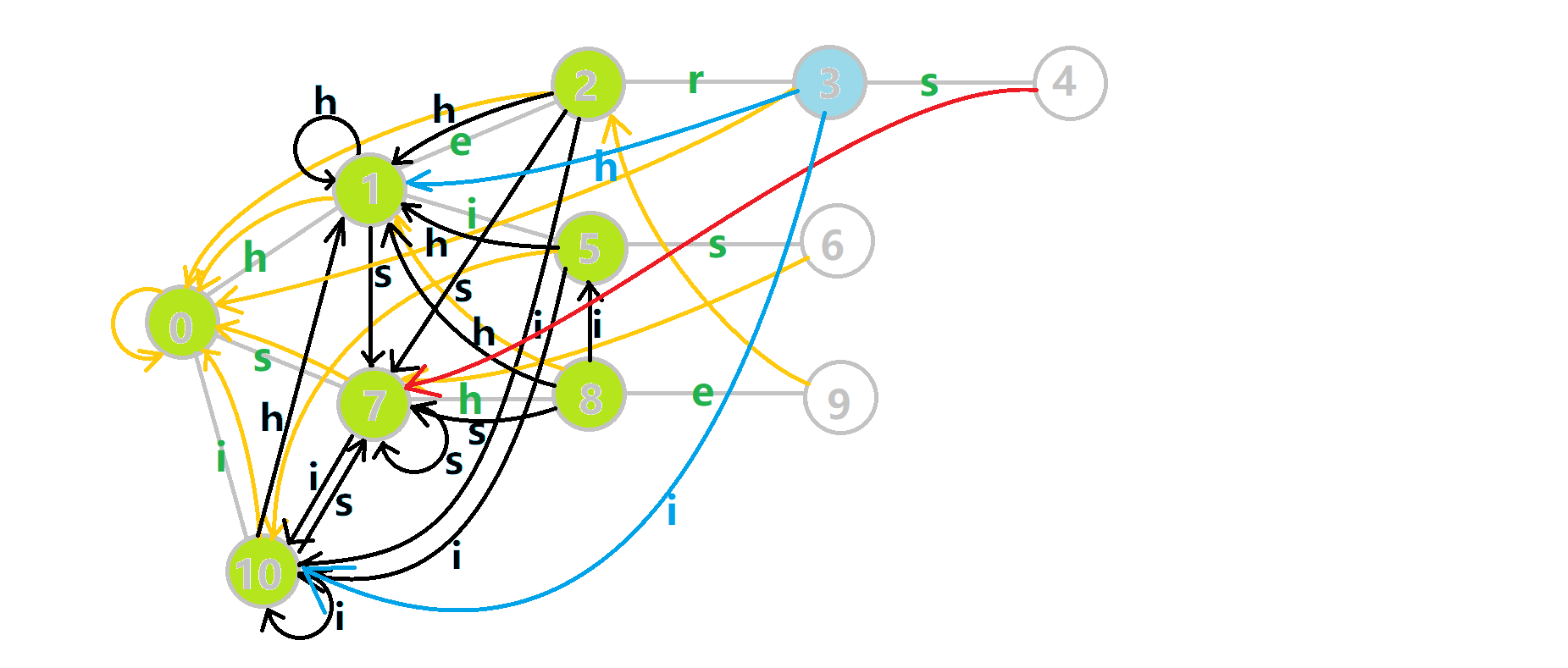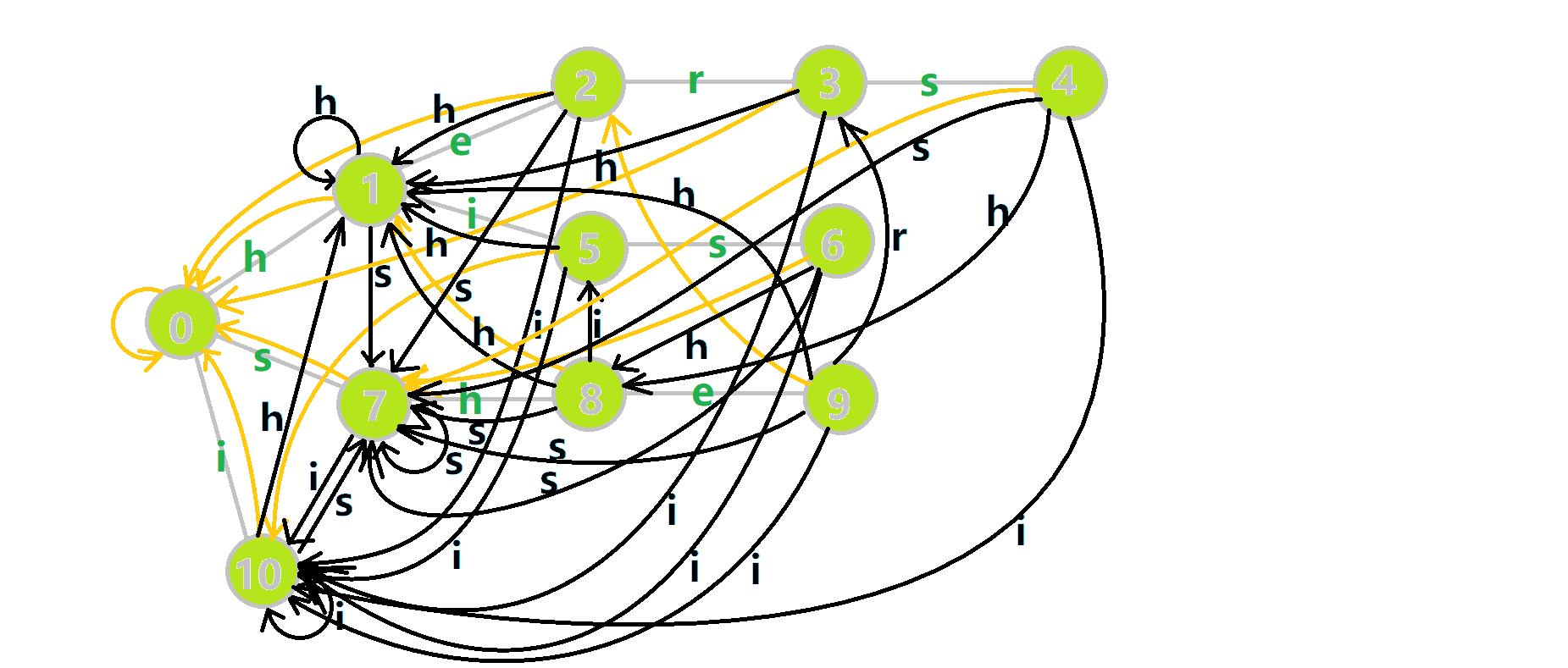
1. 蓝色结点：BFS 遍历到的结点 u
2. 蓝色的边：当前结点下，AC 自动机修改字典树结构连出的边。
3. 黑色的边：AC 自动机修改字典树结构连出的边。
4. 红色的边：当前结点求出的 fail 指针
5. 黄色的边：fail 指针
6. 灰色的边：字典树的边

可以发现，众多交错的黑色边将字典树变成了 字典图 。图中省 s 略了连向根结点的黑边（否则会更乱）。我们重点分析一下结点 5 遍历时的情况。我们求 ( ext{trans}[5][s]=6) 的 fail 指针：

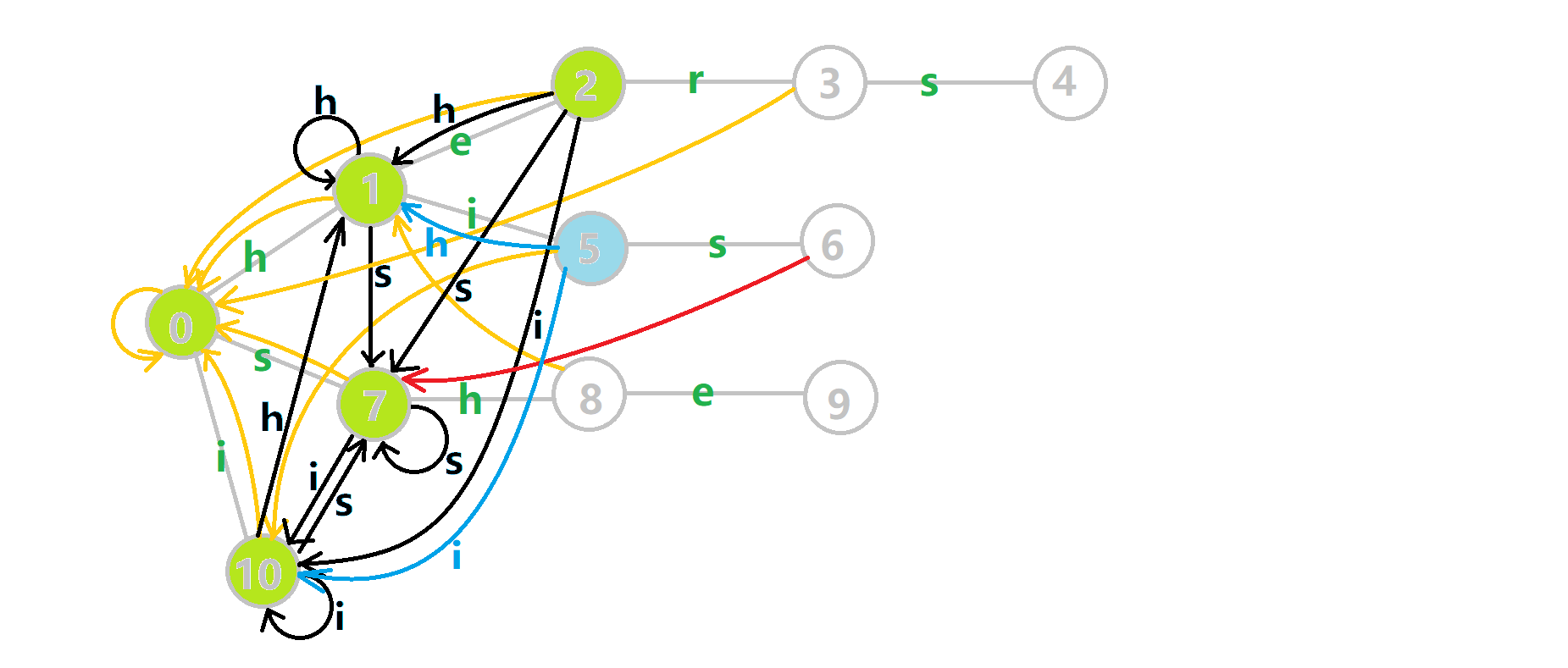
本来的策略是找 fail 指针，于是我们跳到 ( ext{fail}[5]=10) 发现没有 s 连出的字典树的边，于是跳到 ( ext{fail}[10]=0) ，发现有 ( ext{trie}[0][s]=7) ，于是 ( ext{fail}[6]=7) ；但是有了黑边、蓝边，我们跳到 ( ext{fail}[5]=10) 之后直接走 ( ext{trans}[10][s]=7) 就走到 (7) 号结点了。

这就是 build 完成的两件事：构建 fail 指针和建立字典图。这个字典图也会在查询的时候起到关键作用。

多模式匹配

接下来分析匹配函数 query() ：

int query(char *t) {
  int u = 0, res = 0;
  for (int i = 1; t[i]; i++) {
    u = tr[u][t[i] - 'a'];  // 转移
    for (int j = u; j && e[j] != -1; j = fail[j]) {
      res += e[j], e[j] = -1;
    }
  }
  return res;
}

这里 (u) 作为字典树上当前匹配到的结点， res 即返回的答案。循环遍历匹配串， (u) 在字典树上跟踪当前字符。利用 fail 指针找出所有匹配的模式串，累加到答案中。然后清零。对 (e[j]) 取反的操作用来判断 (e[j]) 是否等于 -1。在上文中我们分析过，字典树的结构其实就是一个 trans 函数，而构建好这个函数后，在匹配字符串的过程中，我们会舍弃部分前缀达到最低限度的匹配。fail 指针则指向了更多的匹配状态。最后上一份图。对于刚才的自动机：

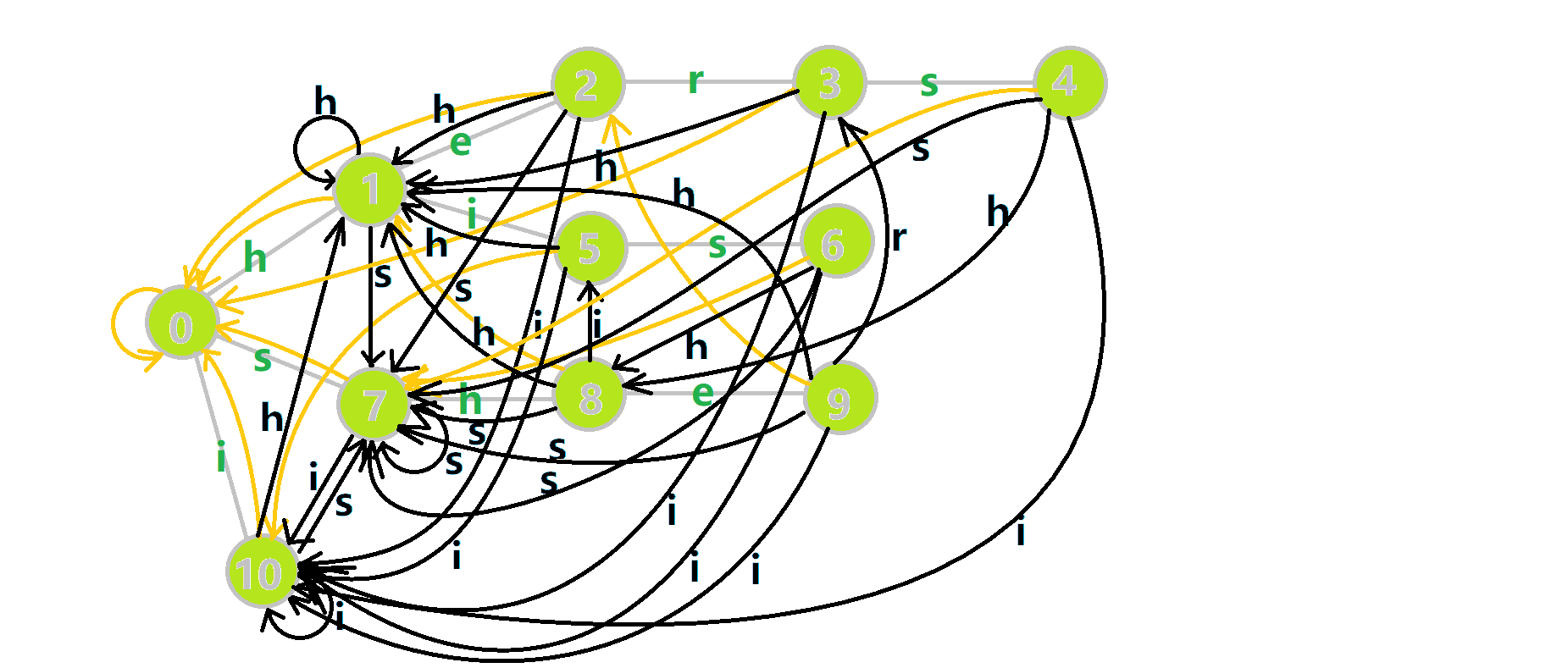
我们从根结点开始尝试匹配 ushersheishis ，那么 (p) 的变化将是：

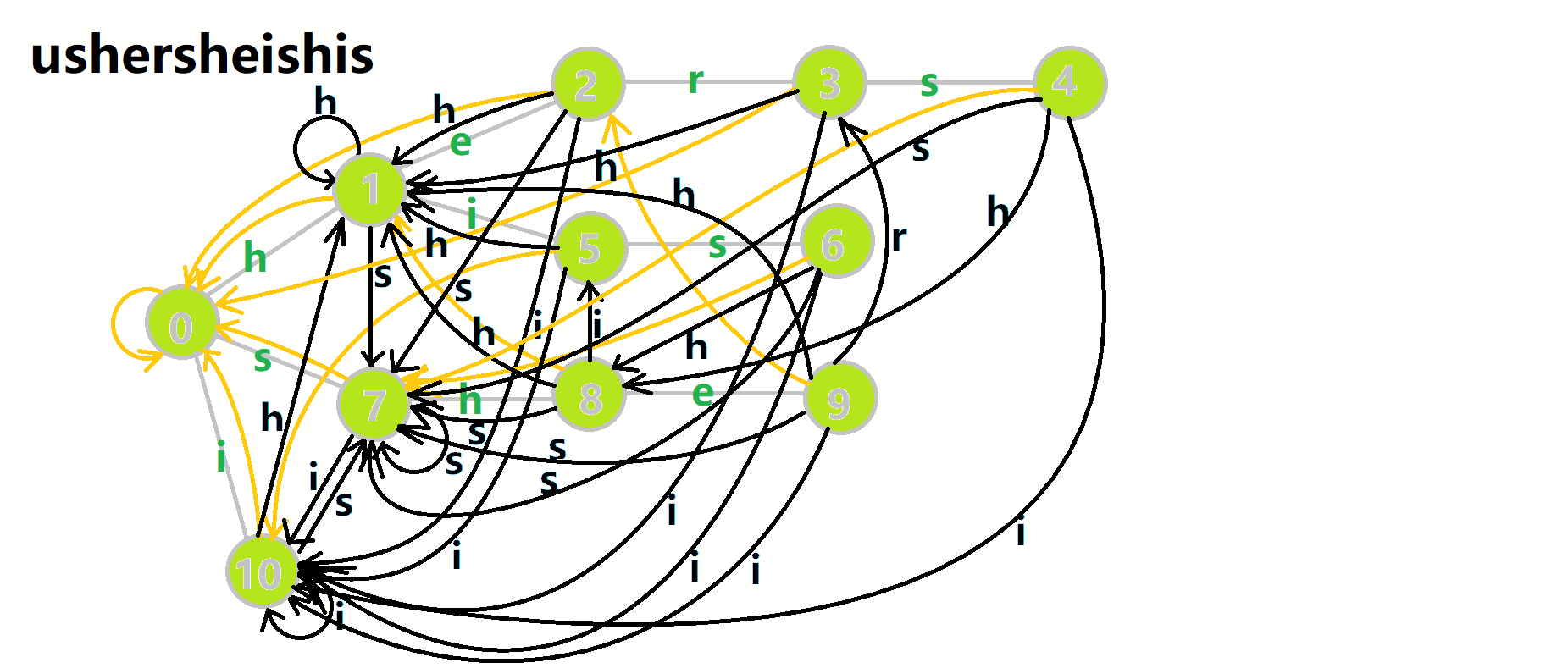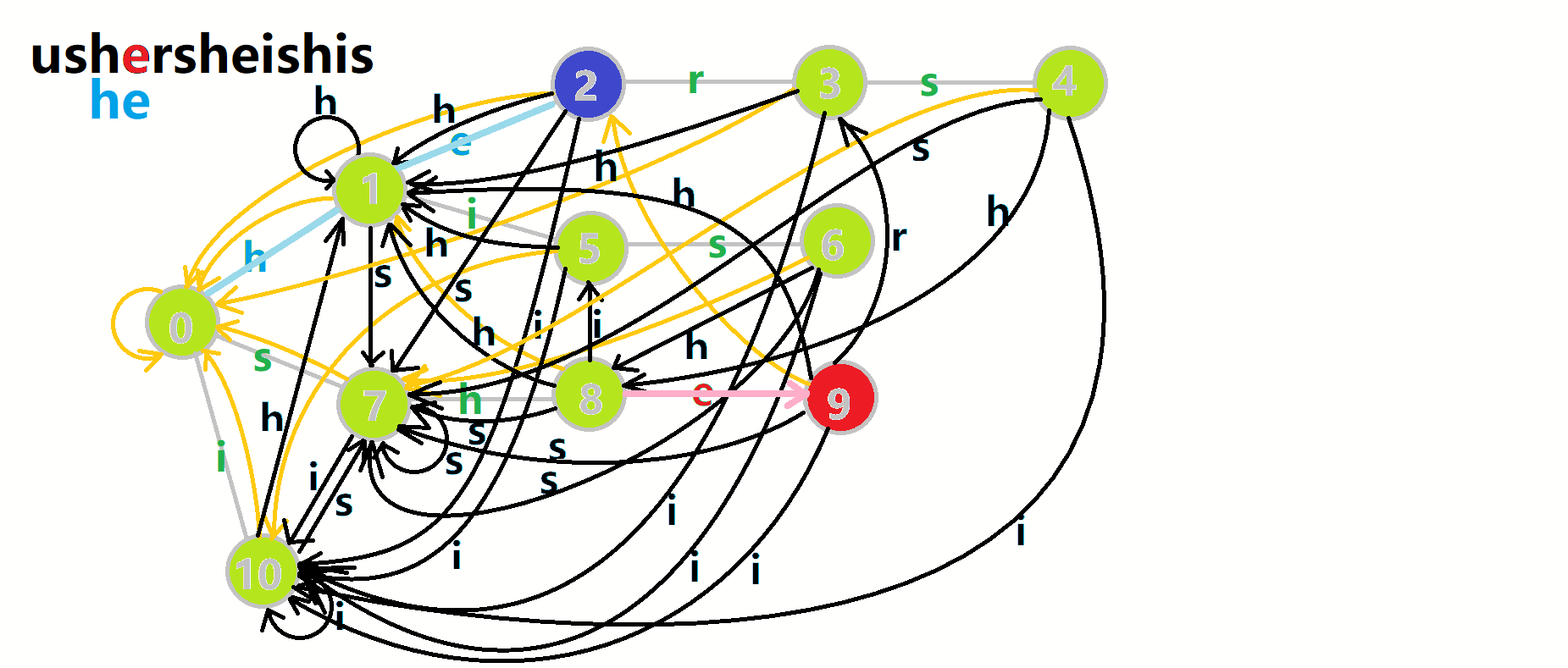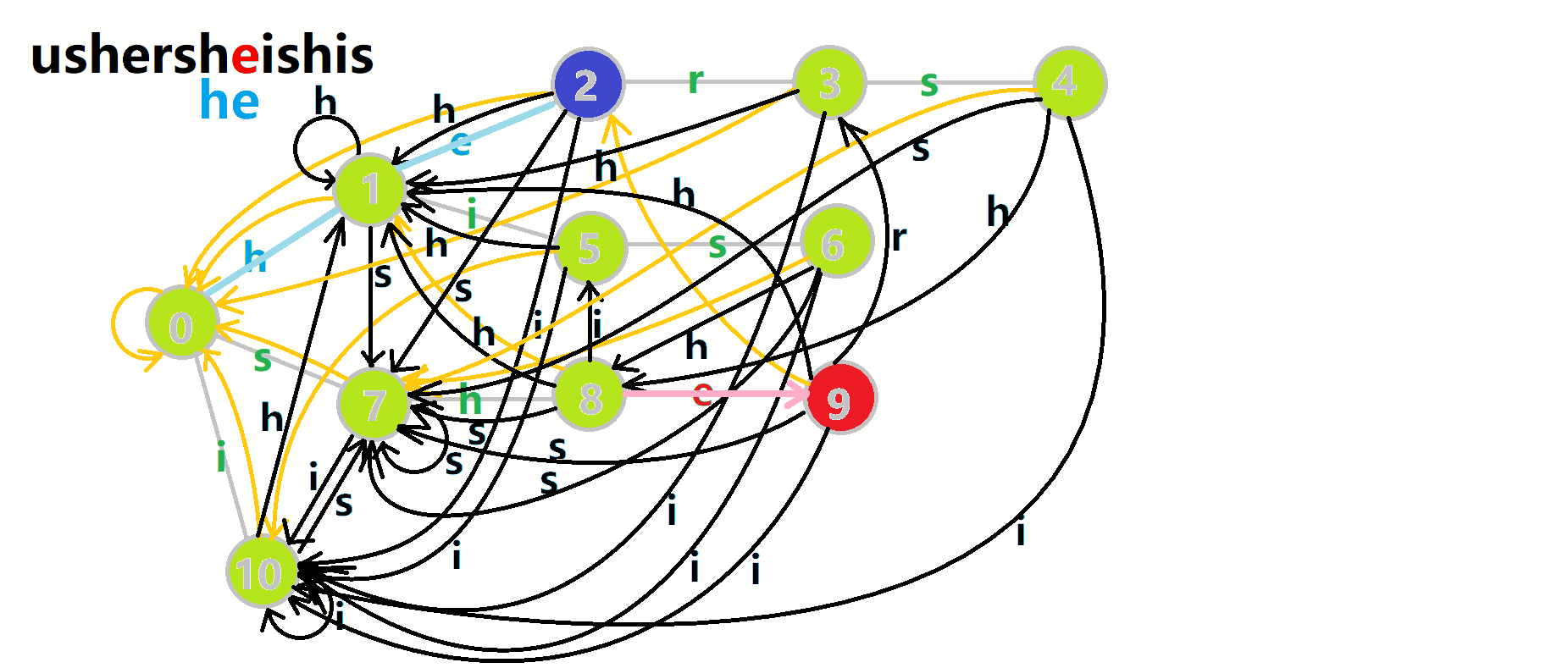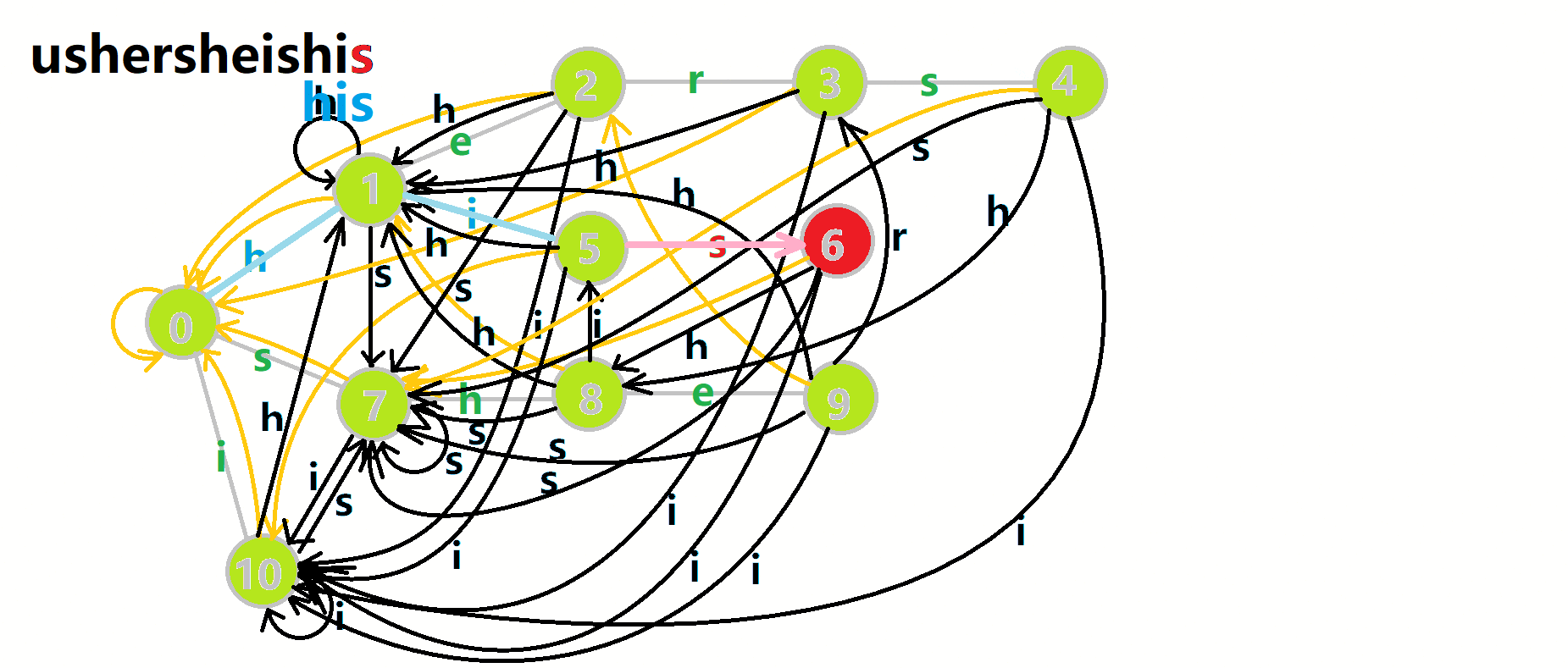
1. 红色结点： (p) 结点
2. 粉色箭头： (p) 在自动机上的跳转，
3. 蓝色的边：成功匹配的模式串
4. 蓝色结点：示跳 fail 指针时的结点（状态）。

总结

希望大家看懂了文章。

时间复杂度：定义 (|s_i|) 是模板串的长度， (|S|) 是文本串的长度， (|Sigma|) 是字符集的大小（常数，一般为 26）。如果连了 trie 图，时间复杂度就是 (O(sum|s_i|+n|Sigma|+|S|)) ，其中 (n) 是 AC 自动机中结点的数目，并且最大可以达到 (O(sum|s_i|)) 。如果不连 trie 图，并且在构建 fail 指针的时候避免遍历到空儿子，时间复杂度就是 (O(sum|s_i|+|S|)) 。

例题

Luogu-P3808【模板】AC 自动机（简单版）

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+6;
int n;
int tr[N][26],tot,e[N],fail[N];
void insert(char *s) {
	int u=0;
	for(int i=1; s[i]; i++) {
		if(!tr[u][s[i]-'a']) {
			tr[u][s[i]-'a']=++tot;
		}
		u=tr[u][s[i]-'a'];
	}
	e[u]++;
}
void build() {
	queue<int> q;
	for(int i=0; i<26; i++) {
		if(tr[0][i]) {
			q.push(tr[0][i]);
		}
	}
	while(q.size()) {
		int u=q.front();
		q.pop();
		for(int i=0; i<26; i++) {
			if(tr[u][i]) {
				fail[tr[u][i]]=tr[fail[u]][i],q.push(tr[u][i]);
			} else {
				tr[u][i]=tr[fail[u]][i];
			}
		}
	}
}
int query(char *s) {
	int u=0,res=0;
	for(int i=1; s[i]; i++) {
		u=tr[u][s[i]-'a'];
		for(int j=u; j&&e[j]^-1; j=fail[j]) {
			res+=e[j],e[j]=-1;
		}
	}
	return res;
}
char s[N];
int main() {
	scanf("%d",&n);
	for(int i=1; i<=n; i++) {
		scanf("%s",s+1),insert(s);
	}
	build(),scanf("%s",s+1),printf("%d",query(s));
	return 0;
}

后记

由 OI-wiki 搬运。