括号的匹配,就是给你一个表达式,比如a {b [c (d + e) / 2 - f ] + 1}, 看看里面的括号是否匹配。怎么看呢?从左到右扫描表达式,遇到左括号{[(,就把它存起来,遇到其它字符,则忽略,遇到右括号时,把前面刚加进去的左括号取出来,看是否匹配。如果匹配,就继续向下走,如果不匹配,就是不匹配了。存什么地方呢?假设存数组。拿a {b [c (d + e) / 2 - f ] + 1} 举例一下,从a开始,向后扫描,a是字符,忽略; { 是左括号,放到数组0位置;b是字符,忽略;[左括号,放到数组1位置;c是字符,忽略;(左括号,放到数组2的位置;d+e都是字符,忽略;)是右字符,这时就要从数组中拿出字符了,拿出哪一个呢?很显然,是拿出位置2中的元素(,匹配吗?()匹配,那继续向下走,同时把2位置处的元素删除;/2-f都是字符,忽略;]右括号,继续从数组中拿出括号,这时要拿位置1处的元素,[,[]匹配,继续向下走,同时把1位置处的元素删除;+1都是字符,忽略;}右括号,继续从数组中拿出括号,这时要拿位置0处的元素{,{}匹配,表达式没有剩下字符了,整个表达式是匹配的。匹配过程中,可以看到左括号添加和取出,顺序是相反的,添加的时候是0,1,2,取出的时候,是2,1,0. 这不就是栈吗?重新描述一下表达式的匹配过程,遇到左括号,push()进栈,遇到右括号,pop()出栈,看pop()出来的元素是否和右括号匹配。
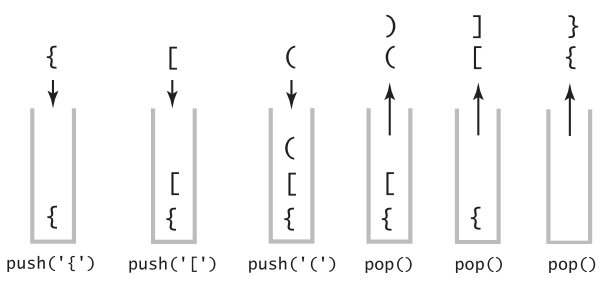
{([都是左括号,push进栈;)是右括号,pop(), (出栈,()匹配;继续 ,]是右括号,pop(),[出栈,[]匹配;继续,}右括号,pop(),{出栈,{}匹配成功;整个表达式也成功了。
再看几个不匹配的表达式,比如{ [ ( ] ) },
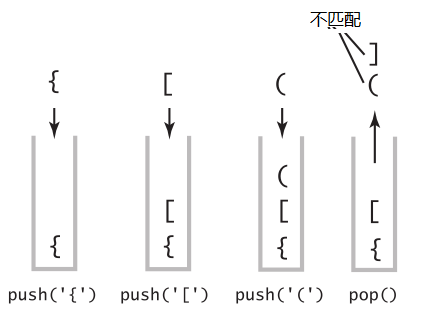
{ [ (依次入栈,碰到],pop(), (出栈,(] 不匹配。再看一个 [ ( ) ] },
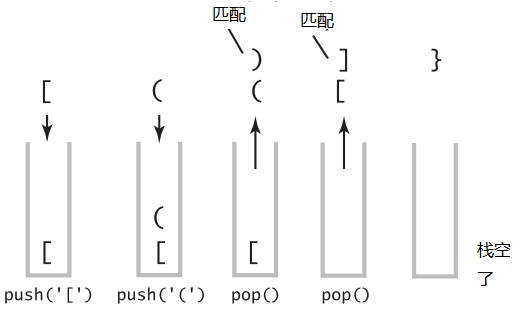
[ (依次入栈,碰到), pop(), (出栈,() 匹配;碰到],pop(), [出栈,[]匹配;碰到},此时,栈为空,不能再pop()了,也就是没有左括号和}匹配。再看{ [ ( ) ],
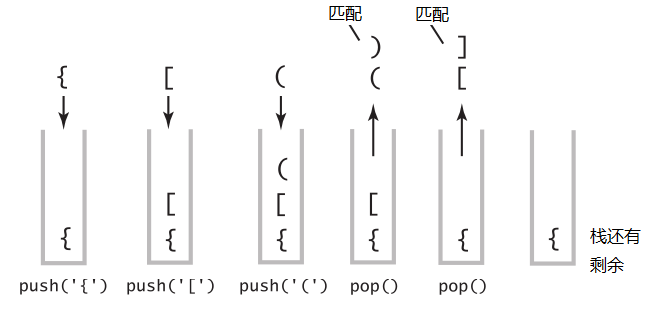
{ [ (依次入栈,) ]依次出栈,都匹配,但是栈中还剩余一个{,也就是没有右括号和它匹配。
经过上面的分析,括号匹配的实现也有点清晰了。创建一个栈,从左右向扫描表达式,就是循环遍历表达式,遇到左括号,调用push()方法入栈,遇到右括号,要先判断栈是否为空,如果为空,那肯定没有对应的左括号,也就不匹配,直接return,不用再循环了。如果栈不为空,调用pop()方法,弹出一个左括号,看是否匹配,如果不匹配,也是return,不用再循环了,如果匹配,再继续循环。如果循环完成了,也是匹配的,但还要判断栈是否为空,如果为空,整个表达式就是匹配的,如果栈不为空,整个表达式是不匹配的。
创建栈,可以使用自己的实现,也可以使用Java提供的LinkedList类,LinkedList实现了栈的API
package dataStructuresAndAbstractions.stack; import java.util.LinkedList; public class BalanceChecker { public static boolean checkBalance(String expression){ LinkedList<Character> openDelimiterStack = new LinkedList<>(); int charCount = expression.length(); boolean isBanlanced = true; int index = 0; char nextChar = ' '; while (isBanlanced && (index < charCount)){ nextChar = expression.charAt(index); switch (nextChar){ case '(': case '{': case '[': openDelimiterStack.push(nextChar); break; case ')': case ']': case '}': if(openDelimiterStack.isEmpty()){ isBanlanced= false; } else { char delimiter = openDelimiterStack.pop(); isBanlanced = isPaired(delimiter, nextChar); } break; } index++; } if (!openDelimiterStack.isEmpty()){ isBanlanced = false; } return isBanlanced; } private static boolean isPaired(char open, char close){ return (open == '(' && close == ')') || (open == '[' && close == ']') || (open == '{' && close == '}'); } public static void main(String[] args) { String expression = "a {b [c (d + e)/2 - f] + 1}"; boolean isBalanced = BalanceChecker.checkBalance(expression); if (isBalanced) System.out.println(expression + " is balanced"); else System.out.println(expression + " is not balanced"); } }
计算带有括号的算术表达式,比如"(1+((2+3)*(4*5)))", 实现的思路是,先创建两个栈,一个是存放操作数字符,一个存放操作符字符,再从左到右循环遍历字符串,忽略左括号,遇到数字,压入到数字字符栈中,遇到操作符,压入到操作符栈中,遇到右括号,弹出一个操作符和两个操作数进行计算,计算完成后,再压入到数字字符栈中,循环完毕,数字栈中只有一个数,这个数就是表达式的计算结果。忽略(,1压入操作数栈,+压入操作符栈。忽略((,2压入操作数栈,+压入操作符栈,3压入操作数栈。
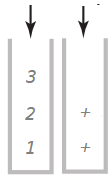
此时遇到了右扩号,弹出2,3,和+,执行3+2,把结果5压入数字栈
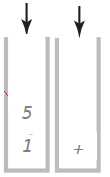
继续向下走,*入操作符栈,忽略(,4压入操作数栈,*压入操作符栈,5压入操作数栈)))

遇到了右扩号,弹出5,4,和*,计算4*5,得出20放入操作数栈中
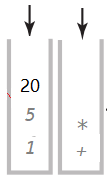
向下走,还是右括号,弹出20,5,和*,把20*5的结果100,放入到操作数栈中
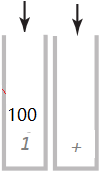
还剩最后一个右括号,再把100,1和+弹出,把结果101放到操作数栈中,

至此,表达式遍历完毕,操作符数栈中,只剩下一个数字,这个数字,就是表达式的计算结果。
import java.util.LinkedList; public class StackEvaluate { public static void main(String[] args) { LinkedList<String> ops = new LinkedList<>(); LinkedList<Double> vals = new LinkedList<>(); String expression = "(1+((2+3)*(4*5)))"; for (int i = 0; i < expression.length(); i++) { String s = expression.charAt(i) + ""; if (s.equals("(")) { ; } else if (s.equals("+") || s.equals("-") || s.equals("*") || s.equals("/")) { ops.push(s); } else if (s.equals(")")) { String op = ops.pop(); double v = vals.pop(); if (op.equals("+")) { v = vals.pop() + v; } else if (op.equals("-")) { v = vals.pop() - v; } else if (op.equals("*")) { v = vals.pop() * v; } else if (op.equals("/")) { v = vals.pop(); } vals.push(v); } else { vals.push(Double.parseDouble(s)); } } System.out.println(vals.pop()); } }