题意:
n叠箱子排成一线,第i叠箱子坐标为xi,竖直方向叠着ai个箱子。
可以花费+1s左移或右移一位,也可以在瞬间搬起一个位置的箱子,或将怀里的有且仅有一个箱子放下。
任意选择起点s(可以不与xi重合),初始时两手空空。
求从s出发,在T秒内,最多能够将多少个箱子集中在s点上。
n<=5e5.
标程:
1 #include<cstdio> 2 #include<algorithm> 3 #include<cstring> 4 using namespace std; 5 typedef long long ll; 6 const int N=500005; 7 ll n,t,x[N],a[N],sum[N],sumk[N],ss,l,r,ans; 8 bool check(ll k) 9 { 10 ll l=1,r=lower_bound(sum+1,sum+n+1,k)-sum; 11 ll lc=a[1],rc=k-sum[r-1]; 12 for (int i=1;i<=n;i++) 13 { 14 while (l<i&&r<=n&&x[i]-x[l]>x[r]-x[i]) 15 { 16 ll mm=min(lc,a[r]-rc); 17 lc-=mm;rc+=mm; 18 if (lc==0) lc=a[++l]; 19 if (rc==a[r]) r++,rc=0; 20 } 21 ss=sumk[r-1]-sumk[i]-x[i]*(sum[r-1]-sum[i]) + x[i]*(sum[i]-sum[l])-(sumk[i]-sumk[l]) 22 +lc*(x[i]-x[l])+rc*(x[r]-x[i]); 23 if (ss<=t) return 1; 24 } 25 return 0; 26 } 27 int main() 28 { 29 scanf("%lld%lld",&n,&t);t/=2; 30 for (int i=1;i<=n;i++) scanf("%lld",&x[i]); 31 for (int i=1;i<=n;i++) scanf("%lld",&a[i]),sum[i]=sum[i-1]+a[i],sumk[i]=sumk[i-1]+a[i]*x[i]; 32 l=1;r=sum[n]; 33 while (l<=r) 34 { 35 ll mid=(l+r)>>1; 36 if (check(mid)) l=mid+1,ans=mid;else r=mid-1; 37 } 38 printf("%lld\n",ans); 39 return 0; 40 }
题解:双指针+二分答案
直接双指针扫描不行吗?因为x坐标并不连续,而且有ai限制,所以选取区间左右端点不一定单调!我们希望能够转换问题。
二分答案取k个物品,如果存在一个S,使得S选取与之距离最近的k个物品时间花费<=T,那么这个k视为可达。
某性质:在相邻两个xi之间选取的S,在选物区间固定的情况下,花费时间T是一个一次函数(单调)。因而极值一定在有物品的点上,对于S只用枚举关键点即可。
这样我们就可以用双指针来解决问题了。(我在双指针这里想了好久)
从共选取k个物品入手,左右端点移动相同的长度。
设置lc和rc分别表示l指针指向的那一块取了lc个,最后r指针指向的那一块取了rc个。
如下图所示,当x[i]-x[l]>x[r]-x[i]时,移动左右端点,选择min(lc,a[r]-rc)的长度移动。
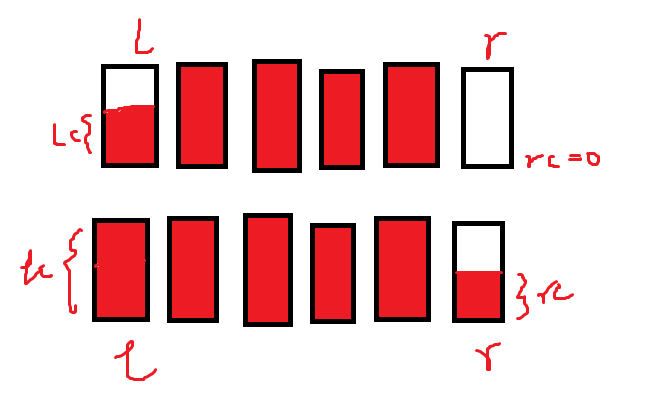
然后用前缀和计算一下所用的时间(注意公式的正确性)。
时间复杂度O(nlog(sum)).