快速查找无序数组中的第K大数？

1.题目分析：

查找无序数组中的第K大数，直观感觉便是先排好序再找到下标为K-1的元素，时间复杂度O(NlgN)。在此，我们想探索是否存在时间复杂度 < O(NlgN)，而且近似等于O(N)的高效算法。

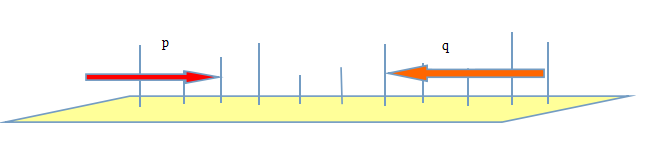
还记得我们快速排序的思想麽？通过“partition”递归划分前后部分。在本问题求解策略中，基于快排的划分函数可以利用“夹击法”，不断从原来的区间[0,n-1]向中间搜索第k大的数，大概搜索方向见下图：

2.参考代码：

 

#include <cstdio>

#define swap(x,y){int temp=x;x=y;y=temp;}

using namespace std;

 

const int maxn=1e5;

int a[maxn];

 

int part(int *arr,int p,int q){

    int i=p-1;

    for(int j=p;j<q;j++) if(arr[j]<a[q]){

        i++;

        swap(arr[i],arr[j]);

    }

    i=i+1;

    swap(arr[i],arr[q]);

    return i;

}

int findK(int *arr,int n,int k){

    int p=0,q=n-1;

    while(p<q){

        //int m=p+(q-p)/2;

        int f=part(arr,p,q);

        //printf("f=%d
",f);   //for tested

        if(f==k){

            return arr[k];

        }else if(f>k){

            q=f-1;

        }else{

            p=f+1;

        }

    }

    return arr[k]; //needed

}

int main(){

    int n,k;

    /*

    *input includes 2 integers. n indicates the num of elements ,

    *k means for the kth larger num to be found

    */

    while(scanf("%d%d",&n,&k)==2){

        for(int i=0;i<n;i++) scanf("%d",&a[i]);

        int ans=findK(a,n,k-1);

        printf("%d
",ans);

    }

    return 0;

}

/*

data for the test:

4 2

1 5433 11 2

4 3

1 5433 11 2

4 4

1 5433 11 2

*/

 

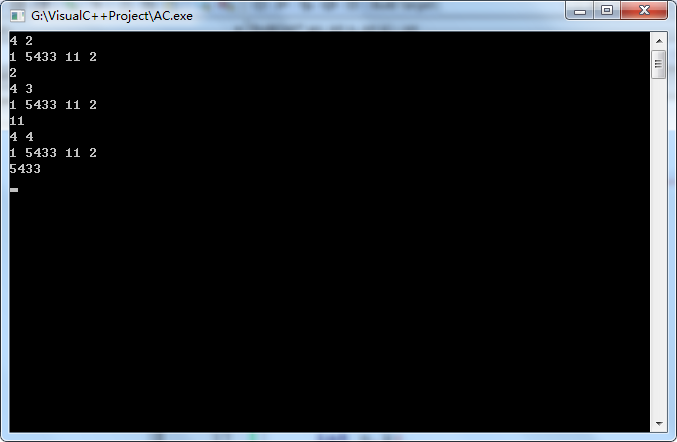
3.测试结果：

 

 

结语：

本算法实现仅适用常规情况，如果K=1或2聪明的你应该要知道不必套用本文的算法，简单遍历保存最大即可，所以说具体问题还得具体分析^_^