本章目的
本章首先引进范数概念,然后介绍矩阵序列及幂级数的收敛定理,在此基础上给出矩阵函数的定义,并介绍其计算。
- 矩阵函数
- 范数
- 矩阵函数的应用
范数

内积与范数

由于范数实际上是表示距离的概念,所以这里的符号记法与之前的模类似。
内积空间中两向量之差的长度固然是这样的一种量,但还可以有其它形式的量。范数是更为一般的反应向量间“距离”的量。
- \(C^n\)中范数的例子:
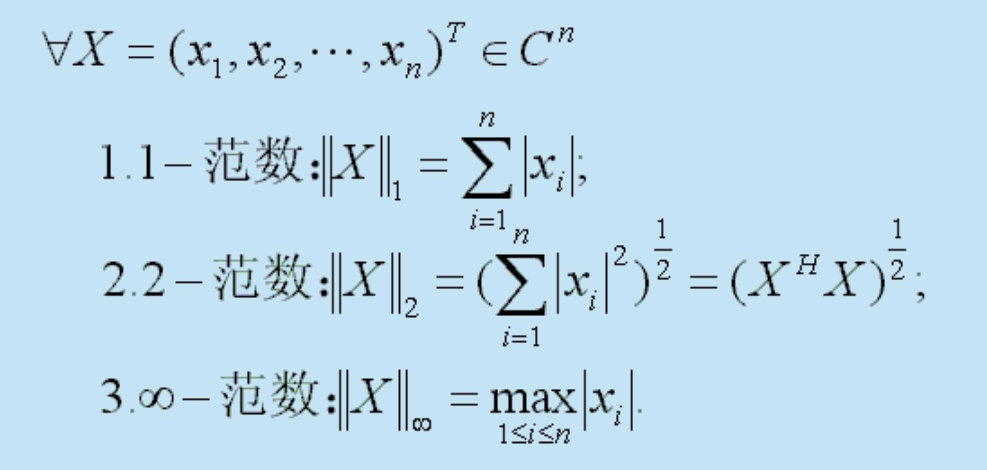

范数与极限

范数的可比较性(等价)

矩阵范数
- 矩阵p-范数:

范数的相容性
- 定义:

- 定理:
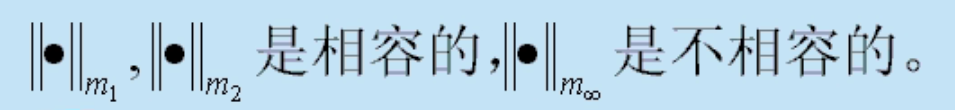
算子范数
- 定义:

- 定理:


- 列模和范数:列取模求和的最大值;
- 谱范数:特征值模的最大值;
- 行模和范数:行取模求和的最大值。
矩阵2-范数(Frobenius范数)和算子2-范数(谱范数)比较重要。
- 例题:
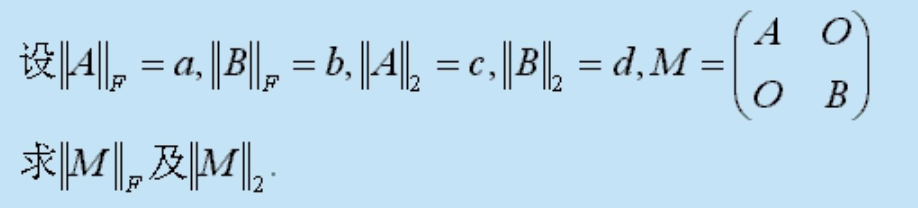
解:\(||M||_F=\sqrt{a^2+b^2}\),\(||M||_2=\max\left\{c,d\right\}\)
收敛定理
- 定义:

幂序列

矩阵幂级数

矩阵函数
定义法

对于比较简单的矩阵,可以直接代入定义中,把矩阵当做x进行计算。
定理
- 定理1:设\(A \in C^{n \times n},\rho(A)<R\),又\(f(x)\)为\(x\)的解析函数\((|x|<R)\),则\(f(A)=Pdiag[f(J_1),\ldots,f(J_s)]P^{-1}\),其中
\[f(J_i)=\begin{bmatrix}
f(\lambda_i) & f^{\prime}(\lambda_i) & \ldots & \frac{f^{(r_i-1)}\ \ (\lambda_i)}{(r_i-1)!} \\
0 & f(\lambda_i) & \ldots & \frac{f^{(r_i-2)}\ \ (\lambda_i)}{(r_i-2)!} \\
\vdots & \vdots & \ & \vdots \\
0 & 0 & \ldots & f^{\prime}(\lambda_i)\\
0 & 0 & \ldots & f(\lambda_i)\\
\end{bmatrix}_{r_i \times r_i}
\]
- 定理2:已知\(n\times n\)矩阵\(A\)的特征值为\(\lambda_1,\lambda_2,\ldots,\lambda_n\),则\(f(A)\)的特征值为\(f(\lambda_1),f(\lambda_2),\ldots,f(\lambda_n)\).
待定系数法

※ 注意:这里几重根就提供几个方程,即求导代入对应的特征值,左右两边相等即可。
关联第三章最小多项式的知识点:最小多项式的根的重数=矩阵的Jordan标准形里以该数为特征值的Jordan块的最高阶数。
因而在待定系数法中往往取阶数最高的Jordan块,因为它涵盖的范围最广、条件最多。找\(g(x)\)的时候应当比最小多项式的次数少1,也就是比最高阶数少1.
矩阵函数的性质
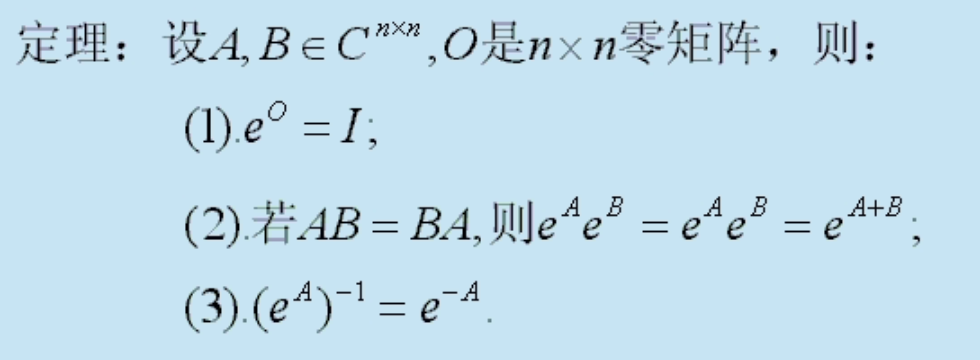
这里要注意第二条一定要满足\(AB=BA\)才可以使用。