BZOJ 1101 [POI2007]Zap ——Dirichlet积

【题目分析】

    Dirichlet积+莫比乌斯函数。

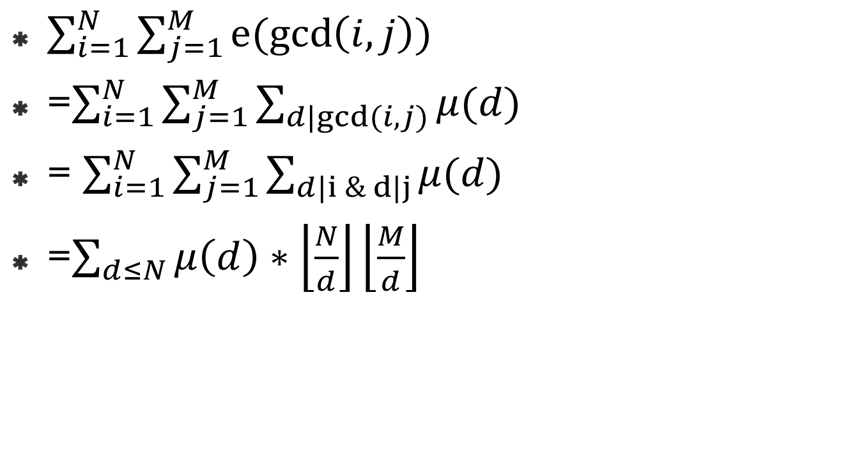
    对于莫比乌斯函数直接筛出处理前缀和。

    对于后面向下取整的部分，可以分成sqrt(n)+sqrt(m)部分分别计算

    学习了一下线性筛法。

    积性函数可以在O(n)的时间内算出。

【代码】

#include <cstdio>
#include <cstring>
#include <cmath>
#include <cstdlib>

#include <map>
#include <set>
#include <queue>
#include <string>
#include <iostream>
#include <algorithm>

using namespace std;

#define maxn 50005
#define inf 0x3f3f3f3f
#define F(i,j,k) for (int i=j;i<=k;++i)
#define D(i,j,k) for (int i=j;i>=k;--i)

void Finout()
{
    #ifndef ONLINE_JUDGE
    freopen("in.txt","r",stdin);
//    freopen("wa.txt","w",stdout);
//    freopen("ac.txt","w",stdout);
    #endif
}

int Getint()
{
    int x=0,f=1; char ch=getchar();
    while (ch<'0'||ch>'9') {if (ch=='-') f=-1; ch=getchar();}
    while (ch>='0'&&ch<='9') {x=x*10+ch-'0'; ch=getchar();}
    return x*f;
}

int pmu[maxn],mu[maxn],vis[maxn],pri[maxn],top=0;

void init()
{
	mu[1]=1;vis[1]=1;
	F(i,2,maxn-1)
	{
		if (!vis[i]) {vis[i]=1;pri[++top]=i;mu[i]=-1;}
		for (int j=1;j<=top&&i*pri[j]<maxn;++j)
		{
			vis[i*pri[j]]=1;
			if (i%pri[j]==0) {break;}
			else mu[pri[j]*i]=-mu[i];
		}
	}
	F(i,1,maxn-1) pmu[i]=pmu[i-1]+mu[i];
}

int t;

int main()
{
	init();
    Finout();
    t=Getint();
    while (t--)
    {
    	int ans=0;
    	int a=Getint(),b=Getint(),d=Getint();
    	a/=d; b/=d;
    	int la,lb,nowa,nowb,l,r=a;
    	while (r)
    	{
//    		cout<<"r is "<<r<<endl;
    		nowa=a/r;nowb=b/r;
    		la=a/(nowa+1)+1;lb=b/(nowb+1)+1;
//    		cout<<"la is "<<la<<" lb is "<<lb<<endl;
    		l=max(la,lb);
    		ans+=nowa*nowb*(pmu[r]-pmu[l-1]);
    		r=l-1;
		}
		printf("%d
",ans);
	}
}