Educational Codeforces Round 86 (Rated for Div. 2) E. Placing Rooks

https://codeforces.com/contest/1342/problem/E

 

 

 

 

 

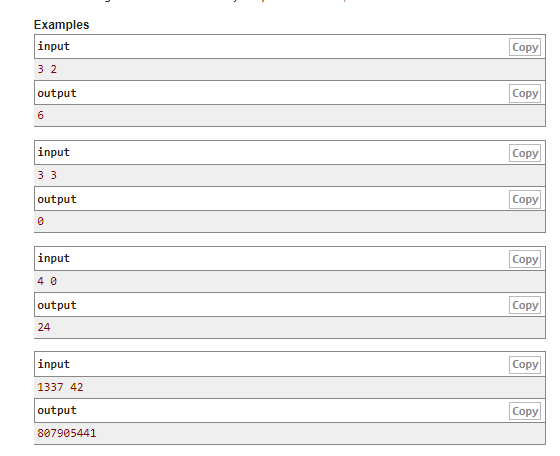
简单叙述一下题意：在一个n*n的国际棋盘上，放置n个车，使得棋盘上的任意格子所在的列或行存在放有一个车（条件一），同时能要正好存在K对车可以无跨越相互攻击到（条件二）。

口胡一波分析思路：首先呢，因为条件一的缘故，所以变换位置的点一定是全部按照行变换或者全部按照列变换，因为如果行和列同时变换，那么，存在某位置不能被攻击到，所以要存在K对车可以相互攻击到，用容斥原理讲就是将分布在N行的点移动到N-K列中，那么就先计算S（n，n-k），也就是计算有多少种方案放入N-K列使得棋盘满足条件一和条件二，然后要考虑选择保留那些列，方案数呢也就是C(N，N-K ） = C(N，K），然后，因为K对车可以相互攻击到，那么也就是说，存在N-K行有车的存在，那么将N-K行做全排列，也就是A（n-k），最后乘起来。对了，因为这里是以行为例，还可以以列为例，那么就要将答案乘2.

 

容斥原理，排列组合，快速幂

 

 

#include <iostream>
#include <algorithm>
#include <cstring>
#include <string>
#include <vector>
#include <map>
#include <set>
#include <list>
#include <deque>
#include <queue>
#include <stack>
#include <cstdlib>
#include <cstdio>
#include <cmath>
#include <iomanip>
#define ull unsigned long long
#define ll long long
#define pb push_back
#define mem(sum,x) memset(sum,x,sizeof(sum))
#define rep(i,start,end) for(int i=start;i<=end;i++)
#define per(i,end,start) for(int i=end;i>=start;i--)
#define tle ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
using namespace std;
const int mod = 998244353;
const int mxn = 1e6+7 ;
ll _,n,k,t,u,v,w,ans,cnt,ok;
ll m[mxn] , num[mxn] , c[mxn] , last[mxn] ;
ll ksm(ll a,ll b)
{
    ll ans = 1 ;
    while(b)
    {
        if(b&1) ans = ans*a%mod;
        a = a*a%mod;
        b>>=1;
    }
    return ans ;
}
ll C(ll n,ll m)
　　{return num[n] * ksm(num[m], mod - 2) % mod * ksm(num[n - m], mod - 2) % mod;}
int main()
{
    tle;
    cin>>n>>k; num[0] = num[1] = 1 ;
    if(k>=n){cout<<0<<endl;return 0 ;}
    rep(i,2,n) num[i] = i*num[i-1]%mod;
    rep(i,0,n-k)
        ans =( ans + ( (n-k-i)%2?-1:1)*C(n-k,i)*ksm(i,n)%mod )%mod;
    ans = (ans+mod)%mod;
    if(k!=0) ans*=2;
    cout<<ans*C(n,n-k)%mod<<endl;
}