Tips:
|
中文题目名称 |
奇数码问题 |
树洞 |
まんふは函数 |
|
英文题目与文件名 |
digital |
holes |
function |
|
输入文件名 |
digital.in |
holes.in |
function.in |
|
输出文件名 |
digital.out |
holes.out |
function.out |
|
每个测试点时限 |
1秒 |
1秒 |
1秒 |
|
内存限制 |
256 MB |
256 MB |
256 MB |
|
测试点数目 |
10 |
10 |
10 |
|
每个测试点分值 |
10 |
10 |
10 |
|
结果比较方式 |
全文比较(过滤行末空格及文末回车) |
全文比较(过滤行末空格及文末回车) |
全文比较(过滤行末空格及文末回车) |
|
题目类型 |
传统 |
传统 |
传统 |
Problem
digital(奇数码问题)
Description
你一定玩过八数码游戏,它实际上是在一个33的网格中进行的,1个空格和1~8这8个数字恰好不重不漏地分布在这33的网格中。
例如:
5 2 8
1 3 _
4 6 7
在游戏过程中,可以把空格与其上、下、左、右四个方向之一的数字交换(如果存在)。 例如在上例中,空格可与左、上、下面的数字交换,分别变成:
5 28
5 2 _
5 2 8
1 _ 3
1 3 8
1 3 7
4 6 7
4 6 7
4 6 _
奇数码游戏是它的一个扩展,在一个nn的网格中进行,其中n为奇数,1个空格和1~nn-1这nn-1个数恰好不重不漏地分布在nn的网格中。
空格移动的规则与八数码游戏相同,实际上,八数码就是一个n=3的奇数码游戏。
现在给定两个奇数码游戏的局面,请判断是否存在一种移动空格的方式,使得其中一个局面可以变化到另一个局面。
Input Format
多组数据,对于每组数据:
第1行一个奇整数n。
接下来n行每行n个整数,表示第一个局面。
接下来n行每行n个整数,表示第二个局面。
局面中每个整数都是0~n*n-1之一,其中用0代表空格,其余数值与奇数码游戏中的意义相同,保证这些整数的分布不重不漏。
Output Format
对于每组数据,若两个局面可达,输出TAK,否则输出NIE。
Sample Input
3
1 2 3
0 4 6
7 5 8
1 2 3
4 5 6
7 8 0
1
0
0
Sample Output
TAK
TAK
Hint
数据范围与约定
对于30%的数据,1<=n<=3;
对于60%的数据,1<=n<=50;
对于100%的数据,1<=n<=500,n为奇数,每个测试点不超过10组。
Solution
把矩阵中的所有数依次排成一行,求逆序对数。若起始状态逆序对数与目标状态同奇偶,则可达,否则不可达。
奇数码中的任何移动均不改变上述逆序对数的奇偶性。
那么为什么用逆序对判断呢(雾)。
#include<cmath> #include<cstdio> #include<cstring> int n; int a[250007]; int c[250007]; int res; void merge_sort(int l,int r) { if (l>=r) return; int mid=(l+r)>>1; merge_sort(l,mid); merge_sort(mid+1,r); int i=l,j=mid+1,k=l; while (i<=mid&&j<=r) { if (a[i]<a[j]) c[k++]=a[i++]; else { c[k++]=a[j++]; res=res+mid-i+1; } } while (i<=mid) c[k++]=a[i++]; while (j<=r) c[k++]=a[j++]; for (int i=l;i<=r;i++) a[i]=c[i]; } int main() { freopen("a.in","r",stdin); while (~scanf("%d",&n)) { memset(a,0,sizeof a); int tot1=0,tot2=0;res=0; for (int i=1;i<=n*n;i++) { int x; scanf("%d",&x); if (x) a[++tot1]=x; } merge_sort(1,tot1); tot1=res;res=0; for (int i=1;i<=n*n;i++) { int x; scanf("%d",&x); if (x) a[++tot2]=x; } merge_sort(1,tot2); tot2=res; res=std::abs(tot1-tot2); if (res&1) printf("NIE "); else printf("TAK "); } }
holes(树洞)
Description
在一片栖息地上有N棵树,每棵树下住着一只兔子,有M条路径连接这些树。更特殊地是,只有一棵树有3条或更多的路径与它相连,其它的树只有1条或2条路径与其相连。换句话讲,这些树和树之间的路径构成一张N个点、M条边的无向连通图,而度数大于2的点至多有1个。
近年以来,栖息地频繁收到人类的侵扰。兔子们联合起来召开了一场会议,决定在其中K棵树上建造树洞。当危险来临时,每只兔子均会同时前往距离它最近的树洞躲避,路程中花费的时间在数值上等于距离。为了在最短的时间内让所有兔子脱离危险,请你安排一种建造树洞的方式,使最后一只到达树洞的兔子所花费的时间尽量少。
Input Format
第一行有3个整数N,M,K,分别表示树(兔子)的个数、路径数、计划建造的树洞数。
接下来M行每行三个整数x,y,表示第x棵树和第y棵树之间有一条路径相连。1<=x,y<=N,x≠y,任意两棵树之间至多只有1条路径。
Output Format
一个整数,表示在最优方案下,最后一只到达树洞的兔子所花费的时间。
sample input
5 5 2
1 2
2 3
3 1
1 4
4 5
sample output
1
Hint
数据范围与约定
对于20%的数据,1 ≤ n ≤ 10。
对于另外30%的数据,每棵树至多与2条路径相连。
对于另外30%的数据,保证存在一种最优解,使与3条或更多路径相连的树上一定建造了树洞。 对于100%的数据,1 ≤ n ≤ 2000,n-1<=m<=n*(n-1)/2。
Solution
求最大值最小,而且答案满足单调,很显然可以用二分
如何验证?
首先考虑一条链的情况,答案必然是(n-k)/k;
而另外存在一个特殊点有三条及以上的边的情况
我们先枚举一个点,可以将特殊点覆盖,覆盖后,
原来的图将断成若干条链,然后重复之前链的做法统计答案
是否超过k,来判断二分的答案是否正确
#include<cstdio> #include<cstring> int n,m,k,rt,deep,mi; int deg[2005],dis[2005]; bool vis[2005],first[2005]; int head[2005],num; struct edge { int next,to; }e[4000005]; void add(int x,int y) { e[++num].next=head[x]; e[num].to=y; head[x]=num; } void dfs(int x,int len) { deep+=1; vis[x]=1; if (!len) return; for (int i=head[x];i;i=e[i].next) { int v=e[i].to; if (!vis[v]) { dis[v]=dis[x]+1; dfs(v,len-1); } } } bool check(int x) { memset(vis,0,sizeof vis); dfs(rt,x); memcpy(first,vis,sizeof vis); for (int i=1;i<=n;i++) { if (first[i]) { int res=0; memset(vis,0,sizeof vis); dfs(i,x); for (int j=1;j<=n&&res<k;j++) if (!vis[j]) { deep=0; dfs(j,n); res+=(deep+2*x)/(2*x+1); } if (res<k) return 1; } } return 0; } int main() { scanf("%d%d%d",&n,&m,&k); for (int i=1;i<=m;i++) { int x,y; scanf("%d%d",&x,&y); deg[x]++,deg[y]++; add(x,y),add(y,x); } for (int i=1;i<=n;i++) if (deg[i]>2) {rt=i;break;} if (!rt) { printf("%d",(n+k-1)/k/2); return 0; } int l=1,r=n-1,ans=n; while (l<=r) { int mid=(l+r)>>1; if (check(mid)) { ans=mid; r=mid-1; } else l=mid+1; } printf("%d",ans); }
function(まんふは函数)
Description
有n个正整数A[1],A[2]…A[n],满足A[i]>=A[i+1]。
它们可以产生n个正整数B[1], B[2] …B[n],其中B[i]=∑j=inA[j]。
まんふは函数(マンフハ函数)f:(Z,Z)→Z定义为:
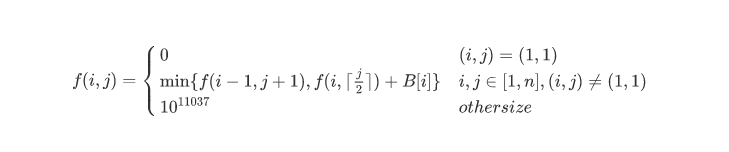
试求f(n,1)。
Input Format
输入包含多组数据,不超过10组。
每组数据的第一行是一个正整数,第二行n个正整数A[i]。
Output Format
对于每组数据,输出一个整数表示f(n,1)。
sample input
3
1 1 1
5
28 26 25 24 1
10
996 901 413 331 259 241 226 209 139 49
sample output
5
233
11037
Hint
对于第一组数据:
f(1,1)=0
f(1,2)=f(1,1)+3=3
f(1,3)=f(1,2)+3=6
f(2,1)=min(f(2,1)+2,f(1,2))=3
f(2,2)=min(f(2,1)+2,f(1,3))=5
f(2,3)=f(2,2)+2=7
f(3,1)=min(f(3,1)+1,f(2,2))=5
对于30%的数据,满足1≤n≤20。
对于60% 的数据,满足1≤n≤1000。
对于 100% 的数据,满足1≤n≤100000,1≤A[i]≤10000。
Solution
题目中要求min{f[n][1]}的值
可以理解成已经合并了n个点,形成1个树的最小值
每次有两个操作一个是将一个点与一棵子树合并,一个是将两棵子树合并
最后要求的是最小值,所以每次合并的值都要最小,
用单调队列去维护这个最小值即可。
#include<cstdio> #include<cstring> int n,x,y,lenu; long long node[100005],unio[100005]; long long top() { if (x<=n&&(y>lenu||node[x]<unio[y])) return node[x++]; return unio[y++]; } int main() { while (~scanf("%d",&n)) { long long ans=0; x=1,y=1,lenu=0; memset(node,0,sizeof node); memset(unio,0,sizeof unio); int tot=n; for (int i=1;i<=n;i++) { int x; scanf("%d",&x); node[tot--]=x; } for (int i=1;i<n;i++) { unio[lenu+1]=top()+top(); ans+=unio[++lenu]; } printf("%lld ",ans); } }