[NOIP2017 提高组] 列队 题解

[NOIP2017 提高组] 列队

有 (n imes m) 的方阵， (k) 次询问，每次从其中取走一个人后向上向左重整队伍，询问取走的人是谁

(n,m,qleq3 imes10^5)

很好的一道动态开点线段树题。

考虑一下，每次取走一个人会发生什么：

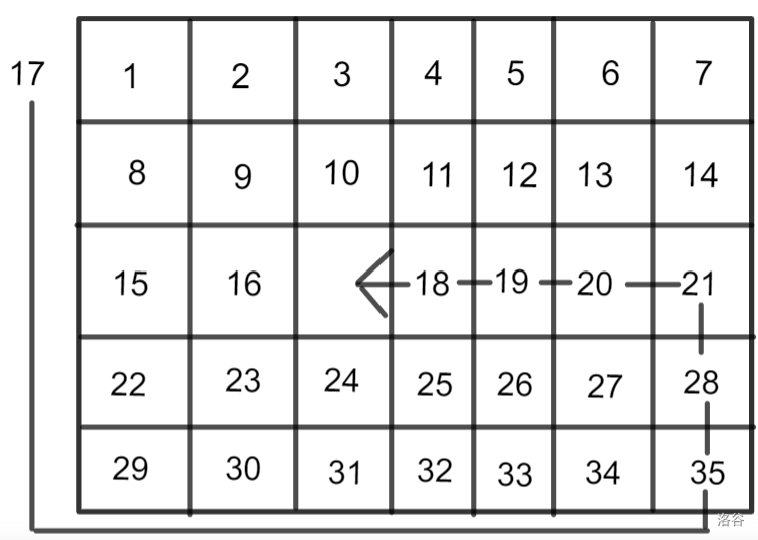
(17) 所在的行，右边的部分全都向左移动一个； 第 (m) 列，从 (17) 所在的列开始全部向上一个。

发现每一行之间都是独立的（除了最后一列）。

这样我们就可以把这个矩阵分割成如下的几块：

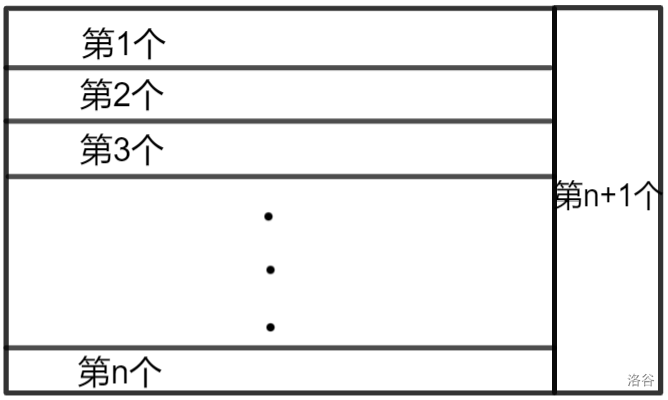
这些部分互相是独立的，可以分别用数据结构来维护。

我们再考虑一下这个数据结构内需要包含什么东西。

• 操作：查询 ((x,y)) 的元素
• 操作：向末尾插入元素

因为我们肯定不能把所有元素都插入到这个数据结构内，所以我们考虑动态开点线段树。

不同于一般的动态开点，这里选择在查询/插入的过程中动态开点以取代低效的建树过程。

具体而言，在查询/插入的时候，直接动态开点，如果它尚无儿子就新建儿子节点。

注意判断，什么时候节点的 (sum) 有值。

#include <bits/stdc++.h>
#define fo(a) freopen(a".in","r",stdin), freopen(a".out","w",stdout)
using namespace std;
const int INF = 0x3f3f3f3f, N = 6e5+5;
typedef long long ll;
typedef unsigned long long ull;
inline ll read(){
	ll ret = 0; char ch = ' ', c = getchar();
	while(!(c >= '0' && c <= '9')) ch = c, c = getchar();
	while(c >= '0' && c <= '9') ret = (ret << 1) + (ret << 3) + c - '0', c = getchar();
	return ch == '-' ? -ret : ret;
}
int n,m,q;
struct Segtre{
	int ls,rs,sum; ll val;
}tr[N<<5];
int tot;
inline int getsum(int id,int l,int r){
	if(id <= n){
		r = min(r,m-1);
		return max(0,r-l+1);
	}
	r = min(r,n);
	return max(0,r-l+1);
}
inline ll getval(ll id,ll l){
	if(id <= n) return (id-1) * m + l;
	else return l*m;
}
inline void pushup(int k){tr[k].sum = tr[tr[k].ls].sum + tr[tr[k].rs].sum;}
ll query(ll id,int k,int l,int r,int x){
	if(l == r)
		return tr[k].sum = 0, tr[k].val;
	int mid = (l + r) >> 1;
	if(!tr[k].ls){
		tr[k].ls = ++tot;
		tr[tr[k].ls].sum = getsum(id,l,mid);
		if(l == mid) tr[tr[k].ls].val = getval(id,l);
	}
	if(!tr[k].rs){
		tr[k].rs = ++tot;
		tr[tr[k].rs].sum = getsum(id,mid+1,r);
		if(r == mid+1) tr[tr[k].rs].val = getval(id,r);
	}
	ll ret = 0;
	if(x <= tr[tr[k].ls].sum) ret = query(id,tr[k].ls,l,mid,x);
	else ret = query(id,tr[k].rs,mid+1,r,x-tr[tr[k].ls].sum);
	pushup(k);
	return ret;
}
void insert(ll id,int k,int l,int r,int x,ll w){
	if(l == r)
		return tr[k].sum = 1, void(tr[k].val = w);
	int mid = (l + r) >> 1;
	if(!tr[k].ls){
		tr[k].ls = ++tot;
		tr[tr[k].ls].sum = getsum(id,l,mid);
		if(l == mid) tr[tr[k].ls].val = getval(id,l);
	}
	if(!tr[k].rs){
		tr[k].rs = ++tot;
		tr[tr[k].rs].sum = getsum(id,mid+1,r);
		if(r == mid+1) tr[tr[k].rs].val = getval(id,r);
	}
	if(x <= mid) insert(id,tr[k].ls,l,mid,x,w);
	else insert(id,tr[k].rs,mid+1,r,x,w);
	pushup(k);
}
signed main(){
//	printf("%.2lf",1.0*sizeof(tr)/1024/1024);
	n = read(), m = read(), q = read();
	tot = n+1; const int siz = max(n,m-1)+q, mx = max(n,m-1);
	for(int i = 1 ; i <= q ; i ++){
		int x = read(), y = read();
		if(y < m){
			ll out = query(x,x,1,siz,y);
			printf("%lld
",out);
			ll in = query(n+1,n+1,1,siz,x);
//			printf(" PUSHIN(%d)
",in);
			insert(x,x,1,siz,mx+i,in);
			insert(n+1,n+1,1,siz,mx+i,out);
		}
		else{
			ll out = query(n+1,n+1,1,siz,x);
			printf("%lld
",out);
			insert(n+1,n+1,1,siz,mx+i,out);
		}
	}
}