| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 337 | Accepted: 123 |
Description
Flood-it is a fascinating puzzle game on Google+ platform. The game interface is like follows:

At the beginning of the game, system will randomly generate an N×N square board and each grid of the board is painted by one of the six colors. The player starts from the top left corner. At each step, he/she selects a color and changes all the grids connected with the top left corner to that specific color. The statement “two grids are connected” means that there is a path between the certain two grids under condition that each pair of adjacent grids on this path is in the same color and shares an edge. In this way the player can flood areas of the board from the starting grid (top left corner) until all of the grids are in same color. The following figure shows the earliest steps of a 4×4 game (colors are labeled in 0 to 5):
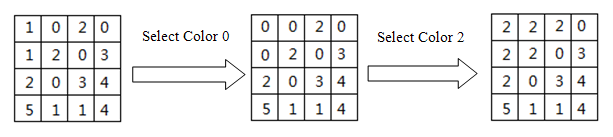
Given a colored board at very beginning, please find the minimal number of steps to win the game (to change all the grids into a same color).

At the beginning of the game, system will randomly generate an N×N square board and each grid of the board is painted by one of the six colors. The player starts from the top left corner. At each step, he/she selects a color and changes all the grids connected with the top left corner to that specific color. The statement “two grids are connected” means that there is a path between the certain two grids under condition that each pair of adjacent grids on this path is in the same color and shares an edge. In this way the player can flood areas of the board from the starting grid (top left corner) until all of the grids are in same color. The following figure shows the earliest steps of a 4×4 game (colors are labeled in 0 to 5):

Given a colored board at very beginning, please find the minimal number of steps to win the game (to change all the grids into a same color).
Input
The input contains no more than 20 test cases. For each test case, the first line contains a single integer N (2<=N<=8) indicating the size of game board.
The following N lines show an N×N matrix (ai,j)n×n representing the game board. ai,j is in the range of 0 to 5 representing the color of the corresponding grid.
The input ends with N = 0.
The following N lines show an N×N matrix (ai,j)n×n representing the game board. ai,j is in the range of 0 to 5 representing the color of the corresponding grid.
The input ends with N = 0.
Output
For each test case, output a single integer representing the minimal number of steps to win the game.
Sample Input
2
0 0
0 0
3
0 1 2
1 1 2
2 2 1
0
Sample Output
0
3
Source
DFS搜索每次染的颜色。无用状态很多,所以需要IDA星算法
估价:统计场上还剩下多少颜色,至少要染这么多次才能出解,如果预估次数加上当前次数超过了当前迭代加深的深度限制,剪枝。
染色:用vis数组标记当前左上角连通块周边的块,每次染色只从这些块儿开始处理。
经历了几次T以后开始标准代码比对,把DFS(当前深度,限制深度)改成DFS(当前深度),函数外存限制;把cpy数组从函数外面拖到里面,就A了。
玄学……?
SilverN at 2018.6.11
神tm玄学,你把cpy设成全局变量,每层搜索共用一个cpy数组,能过样例都是奇迹
真丢人(雾)
1 /*by SilverN*/ 2 #include<iostream> 3 #include<algorithm> 4 #include<cstring> 5 #include<cstdio> 6 #include<cmath> 7 using namespace std; 8 const int mxn=10; 9 int mx[5]={0,1,0,-1,0}; 10 int my[5]={0,0,1,0,-1}; 11 int mp[mxn][mxn]; 12 int vis[mxn][mxn]; 13 int n; 14 //估价函数 15 bool cvis[6]; 16 int pre(){ 17 int res=0; 18 memset(cvis,0,sizeof cvis); 19 for(int i=1;i<=n;i++) 20 for(int j=1;j<=n;j++){ 21 if(vis[i][j]!=1 && !cvis[mp[i][j]]){ 22 cvis[mp[i][j]]=1; res++; 23 } 24 } 25 return res; 26 } 27 //方块染色 28 void change(int x,int y,int c){ 29 vis[x][y]=1;//和左上角同色 30 int i,j; 31 for(i=1;i<=4;i++){ 32 int nx=x+mx[i],ny=y+my[i]; 33 if(nx<1 || nx>n || ny<1 || ny>n)continue;//边界判断 34 if(vis[nx][ny]==1)continue;//访问判断 35 if(mp[nx][ny]==c)change(nx,ny,c); 36 else vis[nx][ny]=2; 37 } 38 return; 39 } 40 bool solve(int color){//尝试染对应颜色 41 bool flag=0; 42 for(int i=1;i<=n;i++) 43 for(int j=1;j<=n;j++){ 44 if(mp[i][j]==color && vis[i][j]==2 ){ 45 change(i,j,color); 46 flag=1;//自带剪枝:如果染这个颜色不能扩大联通范围,就不染 47 } 48 } 49 return flag; 50 } 51 int limit; 52 bool DFS(int now){ 53 if(now==limit)return (pre()==0); 54 if(now+pre()>limit)return 0; 55 int i,j,k; 56 for(k=0;k<=5;k++){ 57 int cpy[9][9]; 58 for(int i=1;i<=n;i++) 59 for(int j=1;j<=n;j++){ 60 cpy[i][j]=vis[i][j]; 61 }//保存状态 62 if(!solve(k))continue; 63 if(DFS(now+1))return 1; 64 for(int i=1;i<=n;i++) 65 for(int j=1;j<=n;j++){ 66 vis[i][j]=cpy[i][j]; 67 }//回溯 68 } 69 return 0; 70 } 71 int main(){ 72 int i,j; 73 while(scanf("%d",&n) && n){ 74 memset(vis,0,sizeof vis); 75 for(i=1;i<=n;i++) 76 for(j=1;j<=n;j++) 77 scanf("%d",&mp[i][j]); 78 change(1,1,mp[1][1]); 79 for(limit=pre();limit;limit++){//迭代加深 80 if(DFS(0))break; 81 } 82 printf("%d ",limit); 83 } 84 return 0; 85 }