题目描述
从前有一个王国,这个王国的城堡是一个矩形,被分为M×N个方格。一些方格是墙,而另一些是空地。这个王国的国王在城堡里设了一些陷阱,每个陷阱占据一块空地。
一天,国王决定在城堡里布置守卫,他希望安排尽量多的守卫。守卫们都是经过严格训练的,所以一旦他们发现同行或同列中有人的话,他们立即向那人射 击。因此,国王希望能够合理地布置守卫,使他们互相之间不能看见,这样他们就不可能互相射击了。守卫们只能被布置在空地上,不能被布置在陷阱或墙上,且一 块空地只能布置一个守卫。如果两个守卫在同一行或同一列,并且他们之间没有墙的话,他们就能互相看见。(守卫就像象棋里的车一样)
你的任务是写一个程序,根据给定的城堡,计算最多可布置多少个守卫,并设计出布置的方案。
输入输出格式
输入格式:第一行两个整数M和N(1≤M,N≤200),表示城堡的规模。
接下来M行N列的整数,描述的是城堡的地形。第i行j列的数用ai,j表示。
ai,j=0,表示方格[i,j]是一块空地;
ai,j=1,表示方格[i,j]是一个陷阱;
ai,j=2,表示方格[i,j]是墙。
输出格式:第一行一个整数K,表示最多可布置K个守卫。
此后K行,每行两个整数xi和yi,描述一个守卫的位置。
输入输出样例
输入样例#1:
3 4 2 0 0 0 2 2 2 1 0 1 0 2
输出样例#1:
2 1 2 3 3
说明
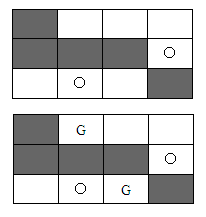
样例数据如图5-2(黑色方格为墙,白色方格为空地,圆圈为陷阱,G表示守卫)
刚开始的写法是BFS出每个联通块,单独处理。
↑明显不对
后来发现可以把被墙隔开的同一行当成两行处理,列同理。
然后二分图匹配坐标即可。
对二分图的理解还是不透彻啊……
(代码仅提供思路,不保证正确性)(没有SPJ程序)
(巴蜀OJ上只要求输出最多守卫数量,已AC)
1 /*By SilverN*/ 2 #include<iostream> 3 #include<cstdio> 4 #include<cmath> 5 #include<cstring> 6 #include<algorithm> 7 #define LL long long 8 using namespace std; 9 const int mxn=2200; 10 int read(){ 11 int x=0,f=1;char ch=getchar(); 12 while(ch<'0' || ch>'9'){if(ch=='-')f=-1;ch=getchar();} 13 while(ch>='0' && ch<='9'){x=x*10+ch-'0';ch=getchar();} 14 return x*f; 15 } 16 struct edge{ 17 int v,nxt; 18 }e[mxn*100]; 19 int hd[mxn*10],mct=0; 20 void add_edge(int u,int v){ 21 e[++mct].v=v;e[mct].nxt=hd[u];hd[u]=mct;return; 22 } 23 int mp[mxn][mxn]; 24 int idx,idy; 25 int hs[mxn][mxn]; 26 int aidx[mxn*10],aidy[mxn*10]; 27 int link[mxn*10],vis[mxn*10]; 28 // 29 int n,m,ans=0; 30 bool DFS(int u){ 31 for(int i=hd[u];i;i=e[i].nxt){ 32 int v=e[i].v; 33 if(!vis[v]){ 34 vis[v]=1; 35 if(link[v]==-1 || DFS(link[v])){ 36 link[v]=u; 37 return 1; 38 } 39 } 40 } 41 return 0; 42 } 43 void solve(){ 44 memset(link,-1,sizeof link); 45 for(int i=1;i<=idx;i++){ 46 memset(vis,0,sizeof vis); 47 if(DFS(i))ans++; 48 } 49 return; 50 } 51 void init(){ 52 int i,j; 53 bool flag=1; 54 for(i=1;i<=m;i++){ 55 flag=1; 56 for(j=1;j<=n;j++){ 57 if(mp[i][j]==2){flag=1;continue;} 58 if(flag){ 59 ++idx; 60 aidx[idx]=i; 61 flag=0; 62 } 63 hs[i][j]=idx; 64 } 65 } 66 idy=idx; 67 for(j=1;j<=n;j++){ 68 flag=1; 69 for(i=1;i<=m;i++){ 70 if(mp[i][j]==2){flag=1;continue;} 71 if(flag){ 72 ++idy; 73 aidy[idy]=j; 74 flag=0; 75 } 76 if(mp[i][j])continue; 77 add_edge(idy,hs[i][j]); 78 add_edge(hs[i][j],idy); 79 // printf("%d %d:%d ",i,j,idy); 80 } 81 } 82 return; 83 } 84 int main(){ 85 m=read();n=read(); 86 int i,j; 87 for(i=1;i<=m;i++) 88 for(j=1;j<=n;j++) 89 mp[i][j]=read(); 90 init(); 91 solve(); 92 /* for(i=1;i<=m;i++){ 93 for(j=1;j<=n;j++){ 94 printf("%d ",hs[i][j]); 95 } 96 printf(" "); 97 }*/ 98 printf("%d ",ans); 99 for(i=idx+1;i<=idy;i++){ 100 if(link[i]!=-1)printf("%d %d ",aidx[link[i]],aidy[i]); 101 } 102 return 0; 103 }