定义
矩阵，类似于一个二维数组
\[\begin{bmatrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9
\end{bmatrix}
\]
主对角线：对于矩阵 \(A\)，主对角线是指 \(A_{i, i}\) 上的元素
零矩阵：所有元素均为 \(0\)，可计为 \(0_{n \times m}\)
单位矩阵 \(I\)：主对角线元素为 \(1\)，其他元素为 \(0\) 的矩阵
矩阵的逆
设一个矩阵 \(A\)，\(A\) 的逆矩阵 \(P\) 是使得 \(A \times P = I\) 的矩阵
可以用高斯消元的方式来求（暂时不会，先咕咕）没有咕咕！
在用高斯消元把矩阵 \(A\) 变成单位矩阵的时候，再开一个单位矩阵 \(P\)
矩阵 \(A\) 进行什么操作，对矩阵 \(P\) 进行同样的操作
当 \(A\) 操作完时， \(P\) 就是矩阵 \(A\) 的逆
具体的证明没看，反正这样做是对的，时间复杂度 \(O(n^3)\)
矩阵加（减）法
对应位置元素相加减
如，设矩阵 \(A,B\)，有 \(A \pm B = C\)，那么对于 \(C\) 中所有元素都有
\[C_{i, j} = A_{i, j} \pm B_{i, j}
\]
注：矩阵加（减）法只有在矩阵大小相同时才有意义
数乘矩阵：
形式： \(k \times A_{n \times m}\) （其中 \(k\) 是任意一个数）
方式： \(k\) 与矩阵中的每个元素相乘成为新矩阵
矩阵乘法
设 \(A,B\) 两个矩阵，大小分别为 \(P \times M,M \times Q\)，设 \(C = A \times B\)，那么对于 \(C\) 中的每个元素，都有：
\[C_{i, j} = \sum_{k = 1}^{M}A_{i, k} \times B_{k, j}
\]
通俗的讲，在矩阵乘法中，结果 \(C\) 矩阵的第 \(i\) 行第 \(j\) 列的数，就是由矩阵 \(A\) 第 \(i\) 行 \(M\) 个数与矩阵 \(B\) 第 \(j\) 列 \(M\) 个数分别相乘再相加得到的。
矩阵乘法满足结合律，但并不满足交换律
注：矩阵乘法只有在第一个矩阵的列数和第二个矩阵的行数相同时才有意义
几个性质：
- 零矩阵和任何矩阵相乘结果都是零矩阵，即 \(0A = A0 = 0\)
- 一个矩阵 \(A_{n \times n}\) 与单位矩阵 \(I_n\) 相乘，结果仍是 \(A_{n \times n}\)，即 \(AI = A\)
- 矩阵乘法满足结合律，即 \(A(BC) = (AB)C\)
- 并不满足交换律，即 \(AB \ne BA\)
- 满足左分配律， \(A(B+C) = AB+AC\)
- 满足右分配律， \((A+B)C = AC+BC\)
优化
改变枚举顺序（粘个OI-wiki的代码）
经过zhx测试在 \(6\) 中排序中 \(i,k,j\) 和 \(i,j,k\) 是较快的。最慢的运算速度大约是他们的几十倍左右
// 以下文的参考代码为例
inline mat operator*(const mat& T) const {
mat res;
for (int i = 0; i < sz; ++i)
for (int j = 0; j < sz; ++j)
for (int k = 0; k < sz; ++k) {
res.a[i][j] += mul(a[i][k], T.a[k][j]);
res.a[i][j] %= MOD;
}
return res;
}
// 不如
inline mat operator*(const mat& T) const {
mat res;
int r;
for (int i = 0; i < sz; ++i)
for (int k = 0; k < sz; ++k) {
r = a[i][k];
for (int j = 0; j < sz; ++j)
res.a[i][j] += T.a[k][j] * r, res.a[i][j] %= MOD;
}
return res;
}
实现
采用二维数组模拟矩阵
为了使用方便，通常把矩阵封装到一个结构体里，并重新定义矩阵运算
参考代码：
struct Matrix{
int n, m;
int a[size][size];
Matrix(){ n = 0, m = 0, memset(a, 0, sizeof a); }
Matrix operator + (const Matrix &b) const{
Matrix res;
res.n = n, res.m = m;
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= m; ++j)
res.a[i][j] = a[i][j] + b.a[i][j];
return res;
}
Matrix operator - (const Matrix &b) const{
Matrix res;
res.n = n, res.m = m;
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= m; ++j)
res.a[i][j] = a[i][j] - b.a[i][j];
return res;
}
Matrix operator * (const Matrix &b) const{
Matrix res;
res.n = n, res.m = b.m; // zhu yi zhe li yu +/- you suo qu bie
for(int i = 1; i <= res.n; ++i)
for(int j = 1; j <= res.m; ++j)
for(int k = 1; k <= m; ++k)
res.a[i][j] = (res.a[i][j] + a[i][k] * b.a[k][j]) % mod;
return res;
}
// 循环时间 与 循环顺序 有关，其中 i,j,k 和 i,k,j 较快
};
矩阵快速幂
其实和普通快速幂没啥两样
Code
void quick_pow(int p){
while(p){
if(p & 1) ans = ans * base;
base = base * base;
p >>= 1
}
}
甚至也可以将它封装到结构体内
Matrix operator ^ (const LL x) const{
Matrix res, base;
for(int i = 1; i <= size; ++i) res.a[i][i] = 1;//初始化res矩阵
for(int i = 1; i <= size; ++i)
for(int j = 1; j <= size; ++j)
base.a[i][j] = a[i][j] % mod;
while(x) {
if(x & 1) res = res * base;
base = base * base;
x >>= 1;
}
return res;
}
例题
Code
#include<iostream>
#include<cstdio>
#include<cstring>
#define int long long
using namespace std;
const int mod = 1e9 + 7;
int n, k;
struct Matrix{
int a[101][101];
Matrix() {memset(a, 0, sizeof a);};
Matrix operator * (const Matrix &b) const {
Matrix res;
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= n; ++j)
for(int k = 1; k <= n; ++k)
res.a[i][j] = (res.a[i][j] + a[i][k] * b.a[k][j]) % mod;
return res;
}
}jz, ans;
int read(){
int s = 0, f = 0;
char ch = getchar();
while(!isdigit(ch)) f |= (ch == '-'), ch = getchar();
while(isdigit(ch)) s = (s << 1) + (s << 3) + (ch ^ 48), ch = getchar();
return f ? -s : s;
}
void quick_pow(Matrix jz, int p, int mod){
ans = jz;
for( ; p; p >>= 1){
if(p & 1) ans = ans * jz;
jz = jz * jz;
}
}
signed main()
{
n = read(), k = read();
for(int i = 1; i <= n; ++i) for(int j = 1; j <= n; ++j) jz.a[i][j] = read();
quick_pow(jz, k - 1, mod);
for(int i = 1; i <= n; ++i) {
for(int j = 1; j <= n; ++j){
printf("%lld ", ans.a[i][j]);
}
puts("");
}
return 0;
}
矩阵加速递推
矩阵加速递推斐波那切数列
发现如下关系：
对于第 \(n - 1\) 项，有：
\(\begin{bmatrix} f_{n - 1} & f_{n - 2} \\ 0 & 0 \end{bmatrix}\) \(\times\) \(\begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix}\) \(=\) \(\begin{bmatrix} f_{n} & f_{n - 1} \\ 0 & 0 \end{bmatrix}\)
所以，若求第 \(n\) 项,有
\(\begin{bmatrix} 1 & 1 \\ 0 & 0 \end{bmatrix}\) \(\times\) \({\begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} }^{n - 2}\) \(=\) \(\begin{bmatrix} f_{n} & f_{n - 1} \\ 0 & 0 \end{bmatrix}\)
最后直接输出答案即可，如果 \(n \le 2\) ，直接输出 \(1\)
例题
Code
#include<iostream>
#include<cstdio>
#include<cstring>
#define int long long
using namespace std;
const int mod = 1e9+7;
int n;
struct Matrix{
int a[3][3];
Matrix(){memset(a, 0, sizeof a);}
Matrix operator * (const Matrix &b) const{
Matrix res;
for(int i = 1; i <= 2; ++i)
for(int j = 1; j <= 2; ++j)
for(int k = 1; k <= 2; ++k)
res.a[i][j] = (res.a[i][j] + a[i][k] * b.a[k][j]) % mod;
return res;
}
}ans, base;
int read(){
int s = 0, f = 0;
char ch = getchar();
while(!isdigit(ch)) f |= (ch == '-'), ch = getchar();
while(isdigit(ch)) s = (s << 1) + (s << 3) + (ch ^ 48), ch = getchar();
return f ? -s : s;
}
void quick_pow(int p){
while(p){
if(p & 1) ans = ans * base;
base = base * base;
p >>= 1;
}
}
signed main()
{
n = read();
if(n <= 2) { printf("1"); return 0; }
base.a[1][1] = base.a[1][2] = base.a[2][1] = 1;
base.a[2][2] = 0;
ans.a[1][1] = ans.a[1][2] = 1;
ans.a[2][1] = ans.a[2][2] = 0;
quick_pow(n - 2);
printf("%lld", ans.a[1][1] % mod);
return 0;
}
注意此时的base矩阵为
\[\begin{bmatrix}
1 & 1 & 0 \\
0 & 0 & 1 \\
1 & 0 & 0
\end{bmatrix}
\]
Code
/*
Work by: Suzt_ilymics
Knowledge: ??
Time: O(??)
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define LL long long
#define int long long
#define orz cout<<"lkp AK IOI!"<<endl
using namespace std;
const int MAXN = 1e5+5;
const int INF = 1e9+7;
const int mod = 1e9+7;
struct Matrix{
int a[4][4];
Matrix() { memset(a, 0, sizeof a); }
Matrix operator * (const Matrix &b) const{
Matrix res;
for(int i = 1; i <= 3; ++i)
for(int j = 1; j <= 3; ++j)
for(int k = 1; k <= 3; ++k)
res.a[i][j] = (res.a[i][j] + a[i][k] * b.a[k][j]) % mod;
return res;
}
Matrix operator ^ (const long long x) const{//重载快速幂，手感绝对丝滑
Matrix res, base;
for(int i = 1; i <= 3; ++i) res.a[i][i] = 1;
for(int i = 1; i <= 3; ++i)
for(int j = 1; j <= 3; ++j)
base.a[i][j] = a[i][j];
while(x){
if(x & 1) res = res * base;
base = base * base;
x >>= 1;
}
return res;
}
}jz, base, ans;
int T, n;
int read(){
int s = 0, f = 0;
char ch = getchar();
while(!isdigit(ch)) f |= (ch == '-'), ch = getchar();
while(isdigit(ch)) s = (s << 1) + (s << 3) + ch - '0' , ch = getchar();
return f ? -s : s;
}
signed main()
{
jz.a[1][1] = jz.a[1][2] = jz.a[1][3] = 1;
base.a[1][1] = base.a[2][3] = base.a[1][2] = base.a[3][1] = 1;
T = read();
while(T--){
n = read();
if(n <= 3){ printf("1\n"); continue; }
ans = jz * (base ^ (n - 3));
printf("%lld\n", ans.a[1][1]);
}
return 0;
}
某场模拟赛的 T2
Description：
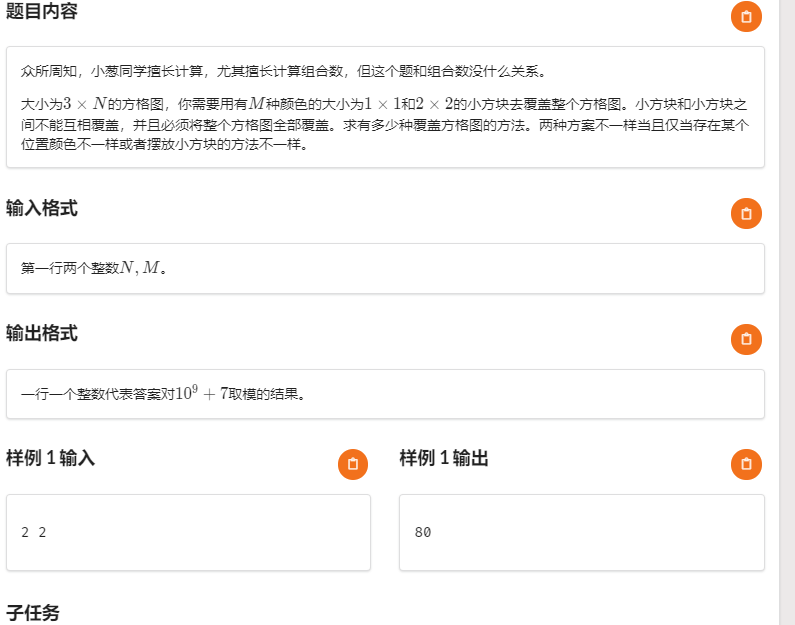
数据范围：\(n,m \le 10^9\)
Solution：
考虑没有颜色的情况：
设 \(f_i\) 表示填到第 \(i\) 列的方案数：
只有两种方块，所以 \(f_i\) 只能从 \(f_{i-1}\) 和 \(f_{i-2}\) 转移过来，考虑转移方案，有转移方程
\[f_{i} = f_{i - 1} + 2 \times f_{i-2}
\]
只有 \(20pts\)，考虑涂上颜色。
因为每种颜色可以随便涂，所以一个方块的方案数为 \(m\)，发现两次转移都会增加三个块，所以方案数要乘以 \(m^3\)，转移方程改为：
\[f_{i} = f_{i-1} \times m^3 + 2 \times f_{i-2} \times m^3
\]
现在有 \(70pts\) 了。
发现这个式子很像斐波那契的递推式啊，考虑矩阵加速。列出相关式子，求出转移矩阵
\[[f_{i-1}, f_{i-2}] \times Base = [f_{i}, f_{i-1}]
\]
其中 \(Base\) 为
\[\begin{bmatrix}
m^3 & 1 \\
2\times m^3 & 0
\end{bmatrix}
\]
矩阵快速幂转移就好了
/*
Work by: Suzt_ilymics
Knowledge: ??
Time: O(??)
f[i] = f[i - 2] * 2 + f[i - 1] // f[i] 表示 到第 i 列 的方案数（不计颜色）
f[i] = f[i - 2] * 2 * m^3 + f[i - 1] * m^3; // 计颜色，两种转移路径都会增加三个方块，每个方块有m种选择方案
1 1
2 0
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define int long long
#define LL long long
#define orz cout<<"lkp AK IOI!"<<endl
using namespace std;
const int MAXN = 1e6+5;
const int INF = 1e9+7;
const int mod = 1e9+7;
struct Matrix {
int a[3][3];
Matrix () { memset(a, 0, sizeof a); }
Matrix operator * (const Matrix &b) {
Matrix res;
for(int i = 1; i <= 2; ++i) {
for(int k = 1; k <= 2; ++k) {
for(int j = 1; j <= 2; ++j) {
res.a[i][j] = (res.a[i][j] + a[i][k] * b.a[k][j]) % mod;
}
}
}
return res;
}
}ans, base;
int n, m, k;
//int f[MAXN];
int read(){
int s = 0, f = 0;
char ch = getchar();
while(!isdigit(ch)) f |= (ch == '-'), ch = getchar();
while(isdigit(ch)) s = (s << 1) + (s << 3) + ch - '0' , ch = getchar();
return f ? -s : s;
}
//void work1() {
// f[1] = 1, f[2] = 3;
// for(int i = 3; i <= n; ++i) f[i] = (2 * f[i - 2] + f[i - 1]) % mod;
// printf("%lld\n", f[n]);
//}
int Quick_Pow(int x, int p, int mod) {
int res = 1;
while(p) {
if(p & 1) res = res * x % mod;
x = x * x % mod;
p >>= 1;
}
return res;
}
Matrix Pow(Matrix x, int p) {
Matrix res;
for(int i = 1; i <= 2; ++i) res.a[i][i] = 1;
while(p) {
if(p & 1) res = res * x;
x = x * x;
p >>= 1;
}
return res;
}
signed main()
{
n = read(), m = read();
// if(m == 1) work1();
// else if(n <= 1000000){
// f[1] = Quick_Pow(m, 3, mod);
// f[2] = Quick_Pow(m, 3, mod) * 2 + Quick_Pow(m, 6, mod);
// for(int i = 3; i <= n; ++i) {
// f[i] = (f[i - 2] * 2 % mod + f[i - 1]) % mod * f[1] % mod;
// }
// printf("%lld\n", f[n]);
// } else {
ans.a[1][1] = (Quick_Pow(m, 3, mod) * 2 + Quick_Pow(m, 6, mod)) % mod;
ans.a[1][2] = Quick_Pow(m, 3, mod);
if(n == 1) {
printf("%lld", ans.a[1][2]);
return 0;
}
if(n == 2) {
printf("%lld", ans.a[1][1]);
return 0;
}
base.a[1][1] = 1 * Quick_Pow(m, 3, mod) % mod, base.a[1][2] = 1;
base.a[2][1] = 2 * Quick_Pow(m, 3, mod) % mod, base.a[2][2] = 0;
Matrix Base = Pow(base, n - 2);
ans = ans * Base;
printf("%lld", ans.a[1][1] % mod);
// }
return 0;
}
/*
100 100
674167999
520955619
*/