写在前面
良心出题人zhx！！！！
暴力分很满，甚至能到200pts+
预估成绩：(100+100+100+70 = 370pts)
最终成绩：(100+100+60+70 = 330pts)
排名：(3/83)
- 排名第三竟只是一个二等？
- 感觉发的耳机贼像机房的耳机，顿时没有鼠标香了/kk
- gryz人均获奖/cy
- 被rk1的jijidawang单调队列了/kk （就评论三楼那位/qq
- 想要rk1的键盘/kel
T1
高精度取模
把字符串倒过来读，边读边取模即可
/*
Work by: Suzt_ilymics
Knowledge: ??
Time: O(??)
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define int long long
#define LL long long
#define orz cout<<"lkp AK IOI!"<<endl
using namespace std;
const int MAXN = 1e6+5;
const int INF = 1e9+7;
const int mod = 1e9+7;
int x = 0, y;
int a[MAXN];
char s[MAXN];
int read(){
int s = 0, f = 0;
char ch = getchar();
while(!isdigit(ch)) f |= (ch == '-'), ch = getchar();
while(isdigit(ch)) s = (s << 1) + (s << 3) + ch - '0' , ch = getchar();
return f ? -s : s;
}
signed main()
{
cin >> (s + 1), y = read();
int len = strlen(s + 1);
for(int i = 1; i <= len; ++i) a[i] = s[len - i + 1] - '0';
if(len == 0) {
for(int i = len; i >= 1; --i) x = x * 10 + a[i];
printf("%lld
", x % y);
} else {
for(int i = len; i >= 1; --i) {
x = x * 10 + a[i];
x %= y;
}
printf("%lld
", x);
}
return 0;
}
T2
Description：
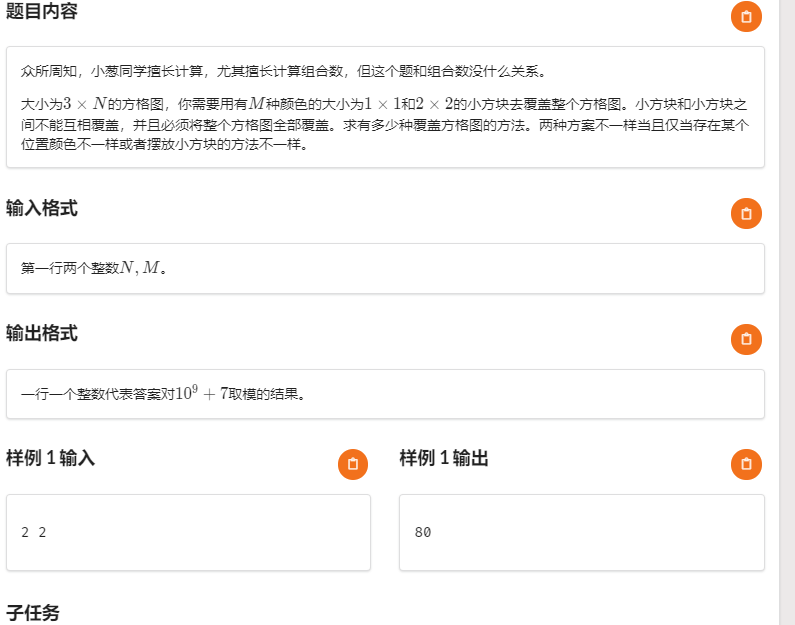
数据范围：(n,m le 10^9)
Solution：
考虑没有颜色的情况：
设 (f_i) 表示填到第 (i) 列的方案数：
只有两种方块，所以 (f_i) 只能从 (f_{i-1}) 和 (f_{i-2}) 转移过来，考虑转移方案，有转移方程
[f_{i} = f_{i - 1} + 2 imes f_{i-2}
]
只有 (20pts)，考虑涂上颜色。
因为每种颜色可以随便涂，所以一个方块的方案数为 (m)，发现两次转移都会增加三个块，所以方案数要乘以 (m^3)，转移方程改为：
[f_{i} = f_{i-1} imes m^3 + 2 imes f_{i-2} imes m^3
]
现在有 (70pts) 了。
发现这个式子很像斐波那契的递推式啊，考虑矩阵加速。列出相关式子，求出转移矩阵
[[f_{i-1}, f_{i-2}] imes Base = [f_{i}, f_{i-1}]
]
其中 (Base) 为
[egin{bmatrix}
m^3 & 1 \
2 imes m^3 & 0
end{bmatrix}
]
矩阵快速幂转移就好了
/*
Work by: Suzt_ilymics
Knowledge: ??
Time: O(??)
f[i] = f[i - 2] * 2 + f[i - 1] // f[i] 表示 到第 i 列 的方案数（不计颜色）
f[i] = f[i - 2] * 2 * m^3 + f[i - 1] * m^3; // 计颜色，两种转移路径都会增加三个方块，每个方块有m种选择方案
1 1
2 0
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define int long long
#define LL long long
#define orz cout<<"lkp AK IOI!"<<endl
using namespace std;
const int MAXN = 1e6+5;
const int INF = 1e9+7;
const int mod = 1e9+7;
struct Matrix {
int a[3][3];
Matrix () { memset(a, 0, sizeof a); }
Matrix operator * (const Matrix &b) {
Matrix res;
for(int i = 1; i <= 2; ++i) {
for(int k = 1; k <= 2; ++k) {
for(int j = 1; j <= 2; ++j) {
res.a[i][j] = (res.a[i][j] + a[i][k] * b.a[k][j]) % mod;
}
}
}
return res;
}
}ans, base;
int n, m, k;
//int f[MAXN];
int read(){
int s = 0, f = 0;
char ch = getchar();
while(!isdigit(ch)) f |= (ch == '-'), ch = getchar();
while(isdigit(ch)) s = (s << 1) + (s << 3) + ch - '0' , ch = getchar();
return f ? -s : s;
}
//void work1() {
// f[1] = 1, f[2] = 3;
// for(int i = 3; i <= n; ++i) f[i] = (2 * f[i - 2] + f[i - 1]) % mod;
// printf("%lld
", f[n]);
//}
int Quick_Pow(int x, int p, int mod) {
int res = 1;
while(p) {
if(p & 1) res = res * x % mod;
x = x * x % mod;
p >>= 1;
}
return res;
}
Matrix Pow(Matrix x, int p) {
Matrix res;
for(int i = 1; i <= 2; ++i) res.a[i][i] = 1;
while(p) {
if(p & 1) res = res * x;
x = x * x;
p >>= 1;
}
return res;
}
signed main()
{
n = read(), m = read();
// if(m == 1) work1();
// else if(n <= 1000000){
// f[1] = Quick_Pow(m, 3, mod);
// f[2] = Quick_Pow(m, 3, mod) * 2 + Quick_Pow(m, 6, mod);
// for(int i = 3; i <= n; ++i) {
// f[i] = (f[i - 2] * 2 % mod + f[i - 1]) % mod * f[1] % mod;
// }
// printf("%lld
", f[n]);
// } else {
ans.a[1][1] = (Quick_Pow(m, 3, mod) * 2 + Quick_Pow(m, 6, mod)) % mod;
ans.a[1][2] = Quick_Pow(m, 3, mod);
if(n == 1) {
printf("%lld", ans.a[1][2]);
return 0;
}
if(n == 2) {
printf("%lld", ans.a[1][1]);
return 0;
}
base.a[1][1] = 1 * Quick_Pow(m, 3, mod) % mod, base.a[1][2] = 1;
base.a[2][1] = 2 * Quick_Pow(m, 3, mod) % mod, base.a[2][2] = 0;
Matrix Base = Pow(base, n - 2);
ans = ans * Base;
printf("%lld", ans.a[1][1] % mod);
// }
return 0;
}
/*
100 100
674167999
520955619
*/
T3
Description
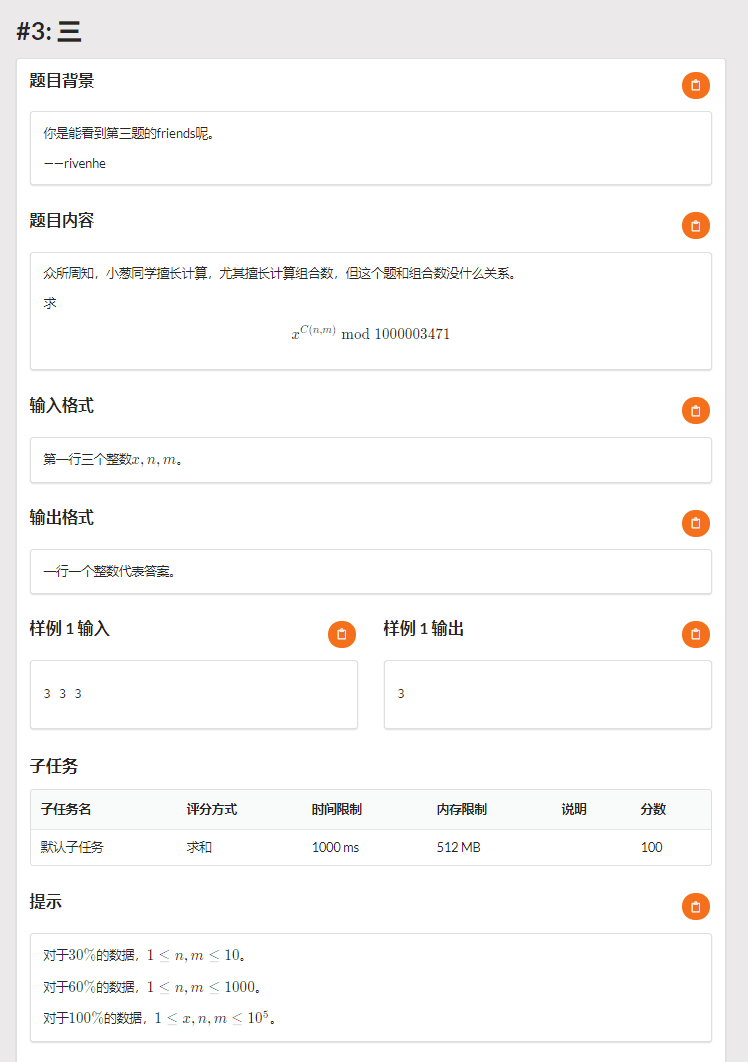
Solution
(C_n^m) 在指数上啊
发现后面的模数是质数，所以可以用欧拉定理取模
但是 (1000003470) 是个合数，没法求逆元，所以我只写了 (n,m le 10^3) 的递推部分/kk
发现 (1000003470) 可以分解为 (2 imes 3 imes 5 imes 53 imes 677 imes 929)
所以对于每个质数求一边，然后用中国剩余定理合并即可（或者用扩展卢卡斯）
嗯，我写挂了
/*
Work by: Suzt_ilymics
Knowledge: ??
Time: O(??)
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define int long long
#define LL long long
#define orz cout<<"lkp AK IOI!"<<endl
using namespace std;
const int MAXN = 1e5+5;
const int INF = 1e9+7;
const int mod = 1000003471; // 这个数是质数
const int phi = 1000003470; // mod 对应的欧拉函数
int tmp[6] = {2, 3, 5, 53, 677, 929};
int x, n, m;
int b[10];
int a[7][1010][1010];
int read(){
int s = 0, f = 0;
char ch = getchar();
while(!isdigit(ch)) f |= (ch == '-'), ch = getchar();
while(isdigit(ch)) s = (s << 1) + (s << 3) + ch - '0' , ch = getchar();
return f ? -s : s;
}
int Gcd(int a, int b) { return !b ? a : Gcd(b, a % b); }
int Lcm(int a, int b) { return a / Gcd(a, b) * b; }
void Merge(int &a1, int &m1, int a2, int m2) {
if(m1 < m2) swap(m1, m2), swap(a1, a2);
while(a1 % m2 != a2) a1 += m1;
m1 = Lcm(m1, m2);
}
int Quick_Pow(int x, int p, int mod) {
int res = 1;
while(p) {
if(p & 1) res = res * x % mod;
x = x * x % mod;
p >>= 1;
}
return res;
}
int C(int n, int m, int p) {
if(n < m) return 0;
return a[p][n][m];
}
int Lucas(int n, int m, int p) {
if(!m) return 1;
if(m > n) return 0;
return Lucas(n / tmp[p], m / tmp[p], p) * C(n % tmp[p], m % tmp[p], p) % tmp[p];
}
void Init() {
for(int i = 0; i < 6; ++i) {
a[i][0][0] = 1;
for(int j = 1; j <= tmp[i]; ++j) {
for(int k = 0; k <= j; ++k) {
a[i][j][k] = a[i][j - 1][k - 1] + a[i][j - 1][k];
if(a[i][j][k] >= tmp[i]) a[i][j][k] -= tmp[i];
}
}
}
}
signed main()
{
Init();
x = read(), n = read(), m = read();
for(int i = 0; i < 6; ++i) b[i] = Lucas(n, m, i);
int v1 = 0, n1 = 1;
for(int i = 0; i < 6; ++i) Merge(v1, n1, b[i], tmp[i]);
printf("%lld", Quick_Pow(x, v1, mod));
return 0;
}
T4
Description
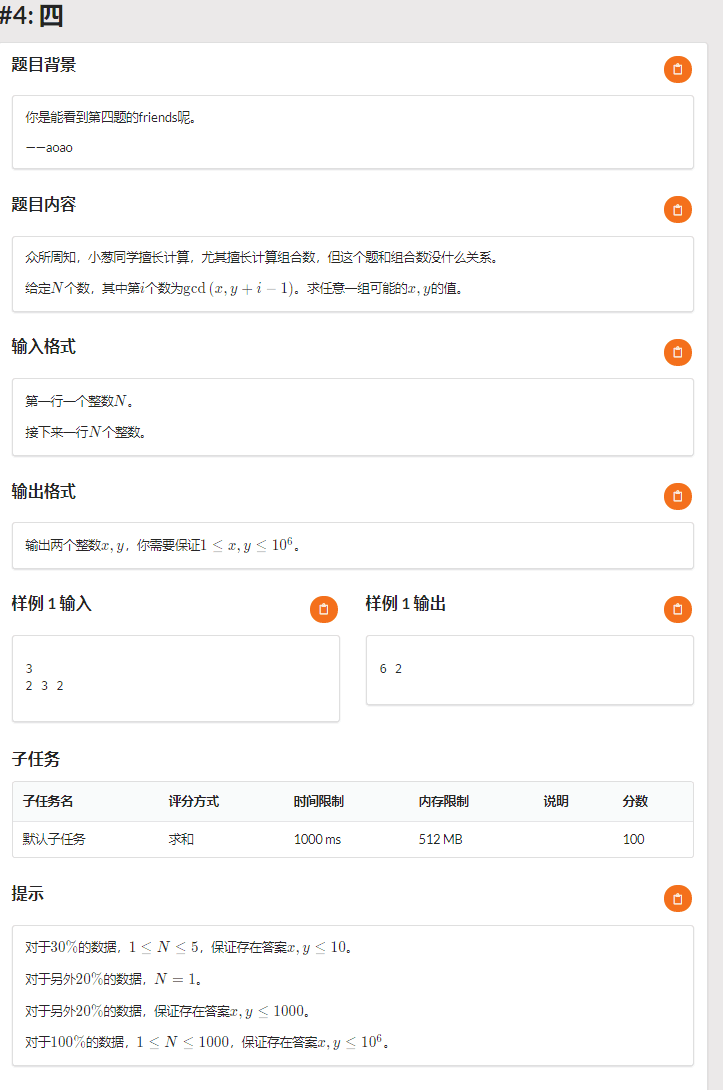
Solution
前三十分暴力判断；
(N = 1) 时输出两遍 (a_1) 即可；
发现 (x) 时不变的，所以存在一个合理的 (x) 是所有 (a_i) 的最小公倍数，又因为保证 (y le 10^3) 然后枚举就变成 (O(n^2)) 的了，可以通过 (70pts)
正解不会了/kk
正解：发现对于每个 (y) 可以写成同余方程的形式，然后解这个同余方程组即可
- (y-i+1) 如果是负数注意转化成正数
/*
Work by: Suzt_ilymics
Knowledge: ??
Time: O(??)
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define LL long long
#define int long long
#define orz cout<<"lkp AK IOI!"<<endl
using namespace std;
const int MAXN = 1e5+5;
const int INF = 1e9+7;
const int mod = 1e9+7;
int n, x = 1, y = 1;
int a[MAXN], b[MAXN];
int read(){
int s = 0, f = 0;
char ch = getchar();
while(!isdigit(ch)) f |= (ch == '-'), ch = getchar();
while(isdigit(ch)) s = (s << 1) + (s << 3) + ch - '0' , ch = getchar();
return f ? -s : s;
}
int Gcd(int a, int b) { return !b ? a : Gcd(b, a % b); }
int Lcm(int a, int b) { return a / Gcd(a, b) * b; }
void Merge(int &a1, int &m1, int a2, int m2) {
if(m1 < m2) swap(m1, m2), swap(a1, a2);
while(a1 % m2 != a2) a1 += m1;
m1 = Lcm(m1, m2);
}
signed main()
{
n = read();
for(int i = 1; i <= n; ++i) a[i] = read();
for(int i = 1; i <= n; ++i) x = Lcm(x, a[i]);
for(int i = 1; i <= n; ++i) b[i] = ((a[i] - i + 1) % a[i] + a[i]) % a[i];
int v1 = 0, n1 = 1;
for(int i = 1; i <= n; ++i) Merge(v1, n1, b[i], a[i]);
printf("%lld %lld", x, v1);
return 0;
}