极角排序,就是平面上有若干点,选一点作为极点,那么每个点有极坐标 (( ho , heta)) ,将它们关于极角 ( heta) 排序。进行极角排序有两种方法。
直接计算极角
我们知道极坐标和直角坐标转换公式中有 ( an heta = frac{y}{x}),所以可以用 (arctan) 来计算。然而 (arctan) 的值域只有 ((-frac{pi}{2},frac{pi}{2})) ,而且当 (x=0) 时无定义,所以需要复杂的分类讨论。
所幸 cmath 中有一个 atan2(y,x) 的函数可以直接计算 (x,y) 的极角,值域是 ((-pi, pi]),所以可以直接用,只不过需要留心第四象限的极角会比第一象限小。
using Points = vector<Point>;
double theta(auto p) { return atan2(p.y, p.x); } // 求极角
void psort(Points &ps, Point c = O) // 极角排序
{
sort(ps.begin(), ps.end(), [&](auto p1, auto p2) {
return lt(theta(p1 - c), theta(p2 - c));
});
}
如果想减少常数,可以提前算出每个点的极角。
利用叉乘
叉乘的正负遵循右手定则,按旋转方向弯曲右手四指,则若拇指向上叉乘为正,拇指向下叉乘为负。也就是说,如果一个向量通过劣角旋转到另一个向量的方向需要按逆时针方向,那么叉乘为正,否则叉乘为负。
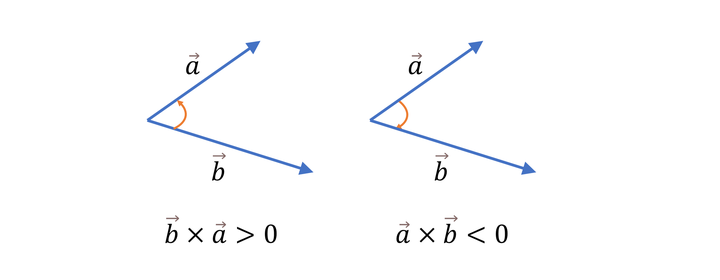
仅靠叉乘是不能进行排序的,因为它不符合偏序关系的条件。如果定义 (vec{x} imes vec{y} < 0) 则 ( heta_{vec{x}} < heta_{vec{y}}),那么我们会发现通过不断在坐标轴上旋转,一个向量的极角最终会小于自己。但是在同一象限内计算叉乘是可以的,所以我们先比较象限再做叉乘。
int qua(auto p) { return lt(p.y, 0) << 1 | lt(p.x, 0) ^ lt(p.y, 0); } // 求象限
void psort(Points &ps, Point c = O) // 极角排序
{
sort(ps.begin(), ps.end(), [&](auto v1, auto v2) {
return qua(v1 - c) < qua(v2 - c) || qua(v1 - c) == qua(v2 - c) && lt(cross(v1 - c, v2 - c), 0);
});
}
我们用0、1、2、3来表示第一、二、三、四象限。
这种方法常数可能稍微大一点,但是精度比较好,如果坐标都是整数的话是完全没有精度损失的。
CF598C Nearest vectors
直接用 atan2 函数算出每个点的极角,然后按照极角从小到大排序,依次比较相邻两个点的差值取最优。
/*
Work by: Suzt_ilymtics
Problem: 不知名屑题
Knowledge: 垃圾算法
Time: O(能过)
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>
#define LL long long
#define LD long double
#define orz cout<<"lkp AK IOI!"<<endl
using namespace std;
const int MAXN = 1e5+5;
const int INF = 1e9+7;
const int mod = 1e9+7;
const LD pi = acos(-1.0);
struct node {
int x, y, id;
LD p;
bool operator < (const node &b) const { return p < b.p; }
}a[MAXN];
int n, ans1 = 0, ans2 = 0;
LD ans;
int read(){
int s = 0, f = 0;
char ch = getchar();
while(!isdigit(ch)) f |= (ch == '-'), ch = getchar();
while(isdigit(ch)) s = (s << 1) + (s << 3) + ch - '0' , ch = getchar();
return f ? -s : s;
}
int main()
{
n = read();
for(int i = 1; i <= n; ++i) {
a[i].x = read(), a[i].y = read(), a[i].id = i;
a[i].p = atan2(a[i].x, a[i].y); // atan2(x, y);
if(a[i].p < 0) a[i].p += 2 * pi;
}
sort(a + 1, a + n + 1);
ans = a[1].p - a[n].p + 2 * pi;
ans1 = a[1].id, ans2 = a[n].id;
for(int i = 2; i <= n; ++i) {
if(a[i].p - a[i - 1].p < ans) {
ans = a[i].p - a[i - 1].p;
ans1 = a[i - 1].id, ans2 = a[i].id;
}
}
printf("%d %d
", ans1, ans2);
return 0;
}
ABC225- E 7
把每个点 ((x,y)) 抽象成一个起点为 ((x,y-1)) 终点为 ((x - 1, y)) 的线段。
然后我们就能算出这些点的极角,按照右端点排序,就转化成了在序列上去最多段不相交的区间的问题,直接贪心即可。
/*
Work by: Suzt_ilymtics
Problem: 不知名屑题
Knowledge: 垃圾算法
Time: O(能过)
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>
#define LL long long
#define LD long double
#define orz cout<<"lkp AK IOI!"<<endl
using namespace std;
const int MAXN = 2e5+5;
const int INF = 1e9+7;
const int mod = 1e9+7;
const LD eps = 1e-10;
struct node {
LD l, r;
node () {}
node (LD a, LD b) { l = a, r = b; }
bool operator < (const node &b) const { return r < b.r; }
}a[MAXN];
int n, ans = 0;
int read(){
int s = 0, f = 0;
char ch = getchar();
while(!isdigit(ch)) f |= (ch == '-'), ch = getchar();
while(isdigit(ch)) s = (s << 1) + (s << 3) + ch - '0' , ch = getchar();
return f ? -s : s;
}
LD Tangent(LD x, LD y) {
if(fabs(x) <= eps) return 1e15;
return y / x;
}
int main()
{
n = read();
for(int i = 1; i <= n; ++i) {
LD x, y;
scanf("%Lf%Lf", &x, &y);
a[i] = node(Tangent(x, y - 1), Tangent(x - 1, y));
}
sort(a + 1, a + n + 1);
LD lst = 0;
for(int i = 1; i <= n; ++i) {
if(a[i].l >= lst) {
ans ++, lst = a[i].r;
}
}
printf("%d", ans);
return 0;
}