[SinGuLaRiTy] NOIP膜你赛-Day 1

【SinGuLRiTy-1022】 Copyright (c) SinGuLaRITy 2017. All Rights Reserved.

 对于所有题目：Time Limit：1s || Memory Limit：256MB 

隔膜 (game)

题目描述

steam 夏季大促销来啦，azui 大爷最近在 steam 上买了 1 mol 的游戏。一天他突然发现了一个搬砖的游戏：

有 N 种砖头，每种砖头有 m 个，每一个的价值为 di 。每一个单位时间你必须搬一块砖，到无砖可搬为止。有一个得分系数 F，初始时为 1。搬一块砖的得分为当时的得分系数 F*di。有 T 个时间分割点。每过一个时间分割点，F会自己加一。例如在时间 p 的得分为 i*di，而在时间p+1的得分为(i+1)*di。

azui大爷觉得这个游戏 too simple，不想去玩，于是让你去帮他上分，希望你能告诉他每局游戏的最大得分。你一定知道这么简单的题目怎么做，快帮帮 azui 大爷吧。

输入

第一行一个数 N。
接下来的 N 行，每行两个数，表示mi和di。
之后的一行一个数 T。
接下来的一行 T 个数，pi。

输出

一个整数，表示最大得分。

样例数据

样例输入	样例输出
2 3 8 5 10 1 20	74

数据范围

1<=N<=100
1<=mi<=10^9
0<=di<=1000
1<=t<=100
1<=p2<p3<…<pt<=10^12

解析

简单的贪心。不过考试的时候有些变量没开long long，直接炸掉......qwq。

Code

#include<cstring>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<iostream>

#define N 110
#define LL unsigned long long

using namespace std;

struct node
{
    LL v;
    LL n;
}kind[N];

LL t[110];
LL ans=0;
LL F=1;

bool cmp(node a,node b)
{
    return a.v<b.v;
}

int main()
{
    LL num;
    cin>>num;
    for(int i=1;i<=num;i++)
    {
        cin>>kind[i].n>>kind[i].v;
    }
    
    LL T;
    cin>>T;
    for(int i=1;i<=T;i++)
    {
        cin>>t[i];
    }
    
    sort(kind+1,kind+num+1,cmp);
    
    LL last_num=0;
    LL start=0;
    LL now_kind=1;
    t[0]=0;
    for(int i=1;i<=T;i++,F++)
    {
        while(start+kind[now_kind].n<=t[i]-t[i-1])
        {
            ans+=kind[now_kind].n*kind[now_kind].v*F;
            start+=kind[now_kind].n;
            now_kind+=1;
            if(now_kind>num)
            {
                cout<<ans;
                return 0;
            }
        }
        ans+=((t[i]-t[i-1])-start)*kind[now_kind].v*F;
        last_num=start+kind[now_kind].n-(t[i]-t[i-1]);
        kind[now_kind].n=last_num;
        start=0;
    }
    for(int i=now_kind;i<=num;i++)
    {
        ans+=kind[i].n*kind[i].v*F;
    }
    cout<<ans;
    return 0;
}

快递配对 (pairing)

题目描述

azui 大爷厌倦了每天在家颓废的生活，于是开始打工送快递。Jeremy 同学不想让 azui 大爷太轻松，于是想让他送快递的路程尽可能的长。
一句话来说就是：给出一棵 n 个点的树，将这 n 个点两两配对，求所有可行的方案中配对两点间的距离的总和最大为多少。

输入

一个数 n (1<=n<=100,000,n 保证为偶数)
接下来 n-1 行每行三个数 x,y,z 表示有一条长度为 z 的边连接x和y  ( 0<=z<=1,000,000,000 )

输出

一个整数，表示距离总和的最大值。

样例数据

样例输入	样例输出
6 1 2 1 1 3 1 1 4 1 3 5 1 4 6 1	7

解析

[树的重心的概念：使树中最大子树(节点最多的子树)中的节点数最小，即把一棵树分为多个size相对"平衡"的子树的节点]

首先我们给出一条结论：要使树中的两个节点之间的路径最长，那么该路径应通过树的重心。换言之，使两个节点分布在重心的两侧，才能得到路径长的最大值。下面给出证明：(论述中的“子树”均指树的重心分离出的子树)

我们由树的重心的定义可以知道，如果一条路径不过树的重心，那么这条路径一定是在同一棵子树里“打转”(因为要通过另外的子树，必须通过树的重心)，如图-1所示。又由于每一棵子树内部的节点较平衡，不存在某棵子树过大的情况，那么两点若都在一棵子树之内，他们之间的路径距离一定是较小的(一定有一条通过重心的路径比它更优秀)。也就是说，较长的路径一定是通过树的重心的。

                                                图-1

现在，既然证明出这个结论，我们会发现：由于节点为偶数个，即不存在多余的节点，那么所有的路径都会通过重心，也就是说，路径和的最大值就是所有节点到树的重心的距离和！后面的操作就比较好办，在此不一一赘述。

<Tips ：由于可能爆栈，需要在main函数中插入以下代码>

int size=16<<20;//16MB
char *p=(char*)malloc(size)+size;
__asm__("movl %0, %%esp
" :: "r"(p));

Code

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<cstdlib>
#include<algorithm>
 
const int MAXN=100005;
typedef long long LL;

using namespace std;

struct node
{
    int e,next;
    LL v;
}h[MAXN*2];

int x,y,n,cnt=1,fir[MAXN]; 
LL z;
int num[MAXN],l[MAXN],r[MAXN]; 
bool vis[MAXN];
 
inline void addedge(int t1,int t2,LL v)
{
    h[++cnt].e=t2;
    h[cnt].next=fir[t1];
    h[cnt].v=v;
    fir[t1]=cnt;
}
 
int dfs(int s)
{
    vis[s]=1; 
    int sum=0;
    for(int i=fir[s];i;i=h[i].next)
        if(!vis[h[i].e]) 
            sum+=dfs(h[i].e)+1;
    return num[s]=sum;
}

int main()
{
    
    int size=16<<20;
    char *p=(char*)malloc(size)+size;
    __asm__("movl %0, %%esp
" :: "r"(p));
    
    cin>>n;
    for(int i=1;i<n;i++)
    {
        cin>>x>>y>>z;
        addedge(x,y,z); 
        addedge(y,x,z);
    }
    dfs(1);
    LL ans=0;
    for(int i=2;i<=cnt;i+=2)
    {
        int s=h[i].e,e=h[i^1].e;
        if(num[s]<num[e])
            swap(s,e);
        LL w=min(num[e]+1,num[1]-num[e]);
        ans+=w*h[i].v;
    }
    cout<<ans;
    return 0;
}

子集 (subset)

题目描述

azui大爷在quack大爷的带领下开始玩集合了，可是他太懒了，不想做quack大爷布置的作业题，便拿来给你做了：
S集合中有n个不同的元素，我们从1-n标号。考虑S 的子集S(i,j)，将这些子集排成一个r行c列矩阵的样子。
◎其中第一行为S(1,1),S(1,2),…,S(1,c)，第二行为S(2,1),S(2,2),..,S(2,c)一直到第r行为S(r,1), S(r,2),…, S(r,c)。
◎这些集合还满足对于在一行中左右相邻的两个集右，左侧是右侧的子集，即S(i,j)∈S(i,j+1)。
◎这些集合还满足对于在一列中上下相邻的两个集合，上方是下方的子集，即S(i,j)∈S(i+1,j)。
问对于S 的全部子集，有多少可能的情况排成上述的矩阵(每个子集可以重复使用)，结果模10^9+7输出。
你一定知道这么简单的题目怎么做，快帮帮azui大爷吧。

输入

一行三个数n,r,c。

输出

一个数表示答案。

样例数据

样例输入	样例输出
1 2 2	6

解析

首先，我们来看一看，当n=1，r=1时，就相当于是在一个一维的序列上，要求该序列后面(右边)的子集要包含前面(左边)的子集，如图-2描述的是此时的一种情况.

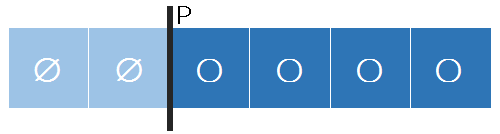
                                图-2

我们发现，当n=1，r=1时，我们实际上只要考虑空集与非空集的分界线(图-2中的P)就行了。此时P的位置aP为后一格的序号，那么其位置的取值范围为 [1,c+1] (当aP=1时，格子里全为非空集；当aP=c+1时，格子里全为空集)。那么对于n=1的情况，答案就为 (c+1) 种。我们又发现其实集合S内的每一个元素是相对独立的，根据乘法原理，我们可以知道，对于n取任意值的情况，答案为 (c+1)^n，此时的计算用快速幂即可。

那么，对于r≠1的其它情况呢？我们可以根据“用P分界”这一思路推而广之，如图-3所示。

                                          

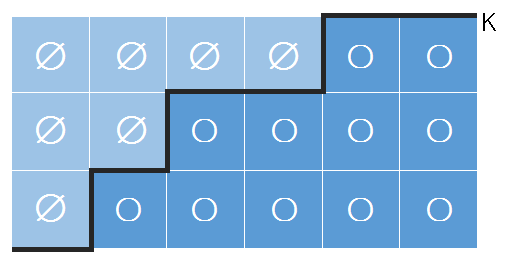
                                图-3                                                                                                          图-4

原来的分界线P变成了折线K，而我们要做的就是计算从左下角到右上角的折线的情况数(如图-4)。那么怎么求呢？由于是从左下角到右上角，可以说我们从左下角开始，向左和向上的“总步数”是一定的，于是就可以用组合数学求解了。

Code

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<cstdlib>
#include<algorithm>
 
typedef long long LL;
const int mod=1e9+7;

using namespace std;
 
LL ksm(LL a,LL k)
{
    LL ans=1;
    while(k)
    {
        if(k&1) 
            ans=ans*a%mod;
        a=a*a%mod; 
        k>>=1;
    }
    return ans;
}

LL jc(int n)
{
    LL ans=1;
    for(int i=2;i<=n;i++)
        ans=ans*i%mod;
    return ans;
}

LL inv(int n)
{
    if(n==1) 
        return 1;
    else 
        return (mod-mod/n*inv(mod%n)%mod)%mod;
}

LL C(int n,int k)
{
    return jc(n)*inv(jc(k))%mod*inv(jc(n-k))%mod;
}

int n,r,c;
int main()
{
    cin>>n>>r>>c;
    cout<<ksm(C(r+c,r),n);
    return 0;
}

Time：2017-07-11