Link Cut Tree学习笔记

最近学习了LCT，这种基于Splay的数据结构真是给人一种优美的感觉啊。

---

简介

Link Cut Tree是一种支持动态加边删边以维护动态森林的数据结构，其核心思想是将一棵树分为若干棵Splay（辅助树），通过对Splay进行操作去维护原树（路径）；

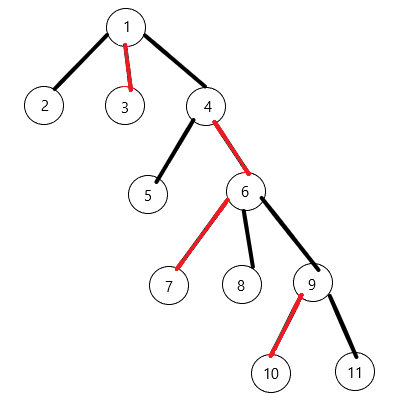
类比于树链剖分中将树剖分为重链，LCT也是将树分为若干条链，其中每一条链都是一棵以节点实际深度为排序关键字的Splay，Splay的根节点指向另一棵Splay；

在一棵Splay（重链）中的边被为重边（偏爱边），连接两棵Splay的边为轻边，如下图，红边为重边：

---

基本操作

1、$ Access（x） $：访问节点$x$，其含义是打通一条从根到$x$的路径，即将这条路径上所有的边变为重边，将所有与这条路径相连的边变为轻边；

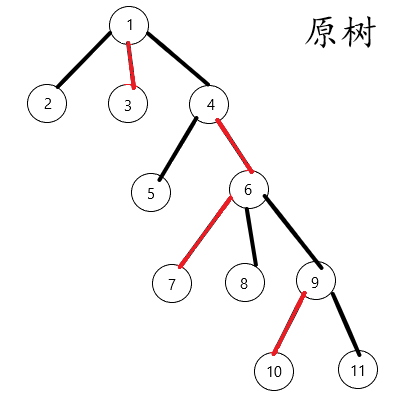
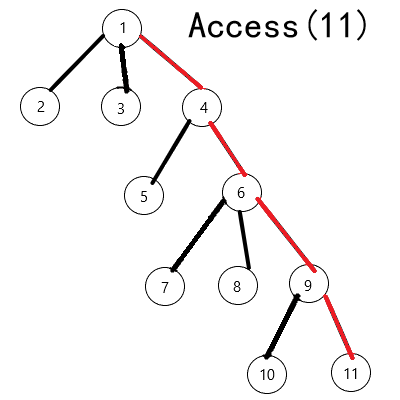
实现：不断将$x$旋转至Splay的根，然后断掉它原来的右儿子相连的边，改为连接$las$（上一个处理的$x$），然后处理$x$的父亲，直至到LCT的树根；

LCT的大部分操作基于$Access$，而$Access$的复杂度是均摊$logn$的，并不会证明orz，可以去看一下杨哲dalao的集训队论文；

void access(int x)
{
    for(int las=0;x;las=x,x=tree[x].fa)
    {
        splay(x),tree[x].son[1]=las;
        pull_up(x);
    }
}

2、$ Make$_$Root（x） $：将$x$作为它所在LCT的树根；

实现：访问$x$，将$x$旋转到根，然后翻转$x$所在的Splay；

关于翻转，因为这里的Splay按照节点实际深度排序，而换根改变了排序键值，因此翻转一下，把链倒过来即可；

void make_root(int x)
{
    access(x),splay(x),reverse(x);
}

3、$ Link（i，j） $：连接$i$，$j$；

实现：将$i$作为树根，然后把$i$父亲赋值为$j$；

void link(int i,int j)
{
    make_root(i),tree[i].fa=j;
}

4、$ Cut（i，j） $：断开连接$i$，$j$的边；

实现：将$i$作为树根，访问$j$，将$j$旋转到根，断开$j$与其左儿子；

$i$与$j$在原树中一定直接相连，辅助树中也是如此，因此访问$j$并旋转后$i$一定是$j$的左儿子；

void cut(int i,int j)
{
    make_root(i),access(j),splay(j);
    tree[i].fa=tree[j].son[0]=0;
    pull_up(j);
}

5、$ Find$_$Root（x） $：查询$x$所在LCT的根；

实现：访问$x$后找到它所在辅助树的第一个节点即可；

int find_root(int x)
{
    access(x),splay(x);
    while(tree[x].son[0])
    {
        x=tree[x].son[0];
    }
    return x;
}

---

模板（题）

2594: [Wc2006]水管局长数据加强版

Time Limit: 25 Sec  Memory Limit: 128 MB
Submit: 4094  Solved: 1272
[Submit][Status][Discuss]

Description

SC省MY市有着庞大的地下水管网络，嘟嘟是MY市的水管局长（就是管水管的啦），嘟嘟作为水管局长的工作就是：每天供水公司可能要将一定量的水从x处送往y处，嘟嘟需要为供水公司找到一条从A至B的水管的路径，接着通过信息化的控制中心通知路径上的水管进入准备送水状态，等到路径上每一条水管都准备好了，供水公司就可以开始送水了。嘟嘟一次只能处理一项送水任务，等到当前的送水任务完成了，才能处理下一项。

在处理每项送水任务之前，路径上的水管都要进行一系列的准备操作，如清洗、消毒等等。嘟嘟在控制中心一声令下，这些水管的准备操作同时开始，但由于各条管道的长度、内径不同，进行准备操作需要的时间可能不同。供水公司总是希望嘟嘟能找到这样一条送水路径，路径上的所有管道全都准备就绪所需要的时间尽量短。嘟嘟希望你能帮助他完成这样的一个选择路径的系统，以满足供水公司的要求。另外，由于MY市的水管年代久远，一些水管会不时出现故障导致不能使用，你的程序必须考虑到这一点。

不妨将MY市的水管网络看作一幅简单无向图（即没有自环或重边）：水管是图中的边，水管的连接处为图中的结点。

Input

输入文件第一行为3个整数：N, M, Q分别表示管道连接处（结点）的数目、目前水管（无向边）的数目，以及你的程序需要处理的任务数目（包括寻找一条满足要求的路径和接受某条水管坏掉的事实）。

以下M行，每行3个整数x, y和t，描述一条对应的水管。x和y表示水管两端结点的编号，t表示准备送水所需要的时间。我们不妨为结点从1至N编号，这样所有的x和y都在范围[1, N]内。

以下Q行，每行描述一项任务。其中第一个整数为k：若k=1则后跟两个整数A和B，表示你需要为供水公司寻找一条满足要求的从A到B的水管路径；若k=2，则后跟两个整数x和y，表示直接连接x和y的水管宣布报废（保证合法，即在此之前直接连接x和y尚未报废的水管一定存在）。

Output

按顺序对应输入文件中每一项k=1的任务，你需要输出一个数字和一个回车/换行符。该数字表示：你寻找到的水管路径中所有管道全都完成准备工作所需要的时间（当然要求最短）。

 

 

最后挂道题吧，LCT维护最小生成树，需要删边；

离线后变为加边，维护路径最大值即可；

AC GET☆DAZE

 

↓代码

#include<algorithm>
#include<iostream>
#include<complex>
#include<cstring>
#include<string>
#include<cstdio>
#include<vector>
#include<cmath>
#include<queue>
#include<map>
#include<set>
#define N 100039
#define mod 20070831
#define inf 0x3f3f3f3f
#define ll long long
using namespace std;
struct question
{
    int opt,i,j,ans;
}ask[N];
struct edge
{
    int u,v,w,des;
}net[N*10];
struct Sinogi
{
    int fa,son[2],w,mx,mr,rev;
}tree[N*15];
int n,m,q,fa[N],des[N];
inline int is_root(int x)
{
    return tree[tree[x].fa].son[0]!=x && tree[tree[x].fa].son[1]!=x;
}
void reverse(int x)
{
    swap(tree[x].son[0],tree[x].son[1]);
    tree[x].rev^=1;
}
void pull_up(int x)
{
    if(tree[tree[x].son[0]].mx>tree[tree[x].son[1]].mx)
    {
        tree[x].mx=tree[tree[x].son[0]].mx;
        tree[x].mr=tree[tree[x].son[0]].mr;
    }
    else
    {
        tree[x].mx=tree[tree[x].son[1]].mx;
        tree[x].mr=tree[tree[x].son[1]].mr;
    }
    if(tree[x].w>tree[x].mx)
    {
        tree[x].mx=tree[x].w,tree[x].mr=x-n;
    }
}
void push_down(int x)
{
    if(tree[x].rev)
    {
        reverse(tree[x].son[0]),reverse(tree[x].son[1]);
        tree[x].rev^=1;
    }
}
void Push_Down(int x)
{
    if(!is_root(x))
    {
        Push_Down(tree[x].fa);
    }
    push_down(x);
}
inline int get(int x)
{
    return tree[tree[x].fa].son[1]==x;
}
void rotate(int x)
{
    int fa=tree[x].fa,wh=get(x);
    if(!is_root(fa))
    {
        tree[tree[fa].fa].son[get(fa)]=x;
    }
    tree[x].fa=tree[fa].fa;
    tree[fa].son[wh]=tree[x].son[wh^1];
    tree[tree[fa].son[wh]].fa=fa;
    tree[x].son[wh^1]=fa;
    tree[fa].fa=x;
    pull_up(fa),pull_up(x);
}
void splay(int x)
{
    Push_Down(x);
    for(int fa=tree[x].fa;!is_root(x);fa=tree[x].fa)
    {
        if(!is_root(fa))
        {
            rotate(get(fa)==get(x) ? fa : x);
        }
        rotate(x);
    }
    pull_up(x);
}
void access(int x)
{
    for(int las=0;x;las=x,x=tree[x].fa)
    {
        splay(x),tree[x].son[1]=las;
        pull_up(x);
    }
}
void make_root(int x)
{
    access(x),splay(x),reverse(x);
}
void link(int i,int j)
{
    make_root(i),tree[i].fa=j;
}
void cut(int i,int j)
{
    make_root(i),access(j),splay(j);
    tree[i].fa=tree[j].son[0]=0;
    pull_up(j);
}
int query_max(int i,int j)
{
    make_root(i),access(j),splay(i);
    return tree[i].mr;
}
bool cmp_u_v(edge a,edge b)
{
    return a.u==b.u ? a.v<b.v : a.u<b.u;
}
bool cmp_w(edge a,edge b)
{
    return a.w<b.w;
}
int search(int i,int j)
{
    int l,r,L,R,mid,res;
    l=1,r=m;
    while(l<=r)
    {
        mid=l+r>>1;
        if(net[mid].u>=i) r=mid-1,L=mid;
        else l=mid+1;
    }
    l=1,r=m;
    while(l<=r)
    {
        mid=l+r>>1;
        if(net[mid].u<=i) l=mid+1,R=mid;
        else r=mid-1;
    }
    while(L<=R)
    {
        mid=L+R>>1;
        if(net[mid].v>=j) R=mid-1,res=mid;
        else L=mid+1;
    }
    return res;
}
int find(int k)
{
    return fa[k]==k ? k : fa[k]=find(fa[k]);
}
void Kruskal()
{
    sort(net+1,net+m+1,cmp_w);
    for(int a=1;a<=n;a++)
    {
        fa[a]=a;
    }
    for(int a=1,b,c;a<=m;a++)
    {
        tree[n+a].w=net[a].w;
        if(net[a].des)
        {
            des[net[a].des]=a;
        }
        else
        {
            b=find(net[a].u),c=find(net[a].v);
            if(b!=c)
            {
                fa[c]=b;
                link(net[a].u,n+a),link(n+a,net[a].v);
            }
        }
    }
}
int main()
{
    int stp;
    scanf("%d%d%d",&n,&m,&q);
    for(int a=1;a<=m;a++)
    {
        scanf("%d%d%d",&net[a].u,&net[a].v,&net[a].w);
        if(net[a].u>net[a].v)
        {
            swap(net[a].u,net[a].v);
        }
    }
    sort(net+1,net+m+1,cmp_u_v);
    for(int a=1;a<=q;a++)
    {
        scanf("%d%d%d",&ask[a].opt,&ask[a].i,&ask[a].j);
        if(ask[a].opt==2)
        {
            if(ask[a].i>ask[a].j)
            {
                swap(ask[a].i,ask[a].j);
            }
            net[search(ask[a].i,ask[a].j)].des=a;
        }
    }
    Kruskal();
    for(int a=q;a>=1;a--)
    {
        stp=query_max(ask[a].i,ask[a].j);
        if(ask[a].opt==1)
        {
            ask[a].ans=net[stp].w;
        }
        else
        {
            if(net[des[a]].w<net[stp].w)
            {
                make_root(net[stp].u),access(net[stp].v),splay(n+stp);
                cut(net[stp].u,n+stp),cut(n+stp,net[stp].v);
                link(ask[a].i,n+des[a]),link(n+des[a],ask[a].j);
            }
        }
    }
    for(int a=1;a<=q;a++)
    {
        if(ask[a].opt==1)
        {
            printf("%d
",ask[a].ans);
        }
    }
    return 0;
}