题目:http://cogs.pw/cogs/problem/problem.php?pid=2533
这道题考察打表观察规律。
发现对f的定义实际是递归式的
f(n,k) = f(0,f(n-1,k))
f(0,k) = balabalabalabala
所以,实际上的f(n,k)是这么个东西
f(0,(0,(0,(0,(0,(0,(0,(0,k))))))))
直接递归求解并打出表来,我们可以发现这样的事实
f(0,k) = k+1
所以有f(n,k) = n + k + 1;
所以题目就转化为了求n+k+1的欧拉函数,直接O(sqrt(n))解决
严谨的数学证明:
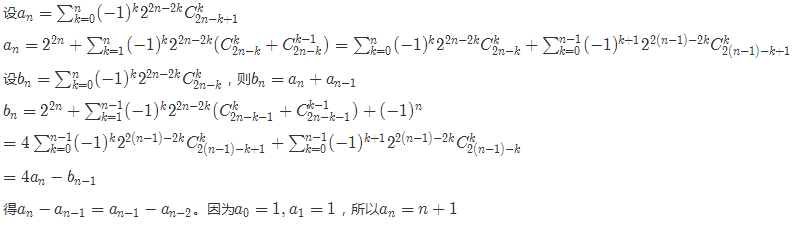
但是这道题其实本人认为最恰当的做法就是打表观察规律
仔仔细细的证明推式子有些得不偿失
1 #include <cmath> 2 #include <queue> 3 #include <cstdio> 4 #include <cstring> 5 #include <iostream> 6 #include <algorithm> 7 using namespace std; 8 typedef long long ll; 9 inline void read(ll &x){ 10 x=0;char ch;bool flag = false; 11 while(ch=getchar(),ch<'!');if(ch == '-') ch=getchar(),flag = true; 12 while(x=10*x+ch-'0',ch=getchar(),ch>'!');if(flag) x=-x; 13 } 14 inline ll cat_max(const ll &a,const ll &b){return a>b ? a:b;} 15 inline ll cat_min(const ll &a,const ll &b){return a<b ? a:b;} 16 inline ll phi(ll x){ 17 ll ret = x; 18 for(ll i=2;i*i<=x;++i){ 19 if(x % i == 0){ 20 ret /= i;ret *= (i-1); 21 while(x % i == 0) x /= i; 22 } 23 } 24 if(x^1) ret /= x,ret *= (x-1); 25 return ret; 26 } 27 int main(){ 28 freopen("skyfuc.in","r",stdin); 29 freopen("skyfuc.out","w",stdout); 30 ll n,x; 31 while(scanf("%lld%lld",&n,&x) != EOF) 32 printf("%lld ",phi(n+x+1)); 33 getchar();getchar(); 34 return 0; 35 }