
#define DeBUG #include <iostream> #include <cstdio> #include <cstring> #include <cmath> #include <cstdlib> #include <algorithm> #include <vector> #include <stack> #include <queue> #include <string> #include <set> #include <sstream> #include <map> #include <bitset> using namespace std ; #define zero {0} #define INF 200000000 #define EPS 1e-6 #define MM 1 typedef long long LL; inline int sgn(double x)//sgn函数符号判断 ,小于给定精度判零 { return fabs(x) < EPS ? 0 :(x < 0 ? -1 : 1); } template<class T> T sqr(T x)//求平方 { return x * x; } struct Point { double x, y;//点对应坐标 Point() {} Point(double x, double y):x(x), y(y) {}//使用两点进行初始化 } ; typedef Point Vec; Vec operator + (Vec a, Vec b)//点加法 { return Vec(a.x + b.x, a.y + b.y); } Vec operator - (Vec a, Vec b)//点减法 { // cout<<a.x<<a.y<<endl; // cout<<b.x<<b.y<<endl; return Vec(a.x - b.x, a.y - b.y); } bool operator == (Point a, Point b)//点相等判断 { return sgn(a.x - b.x) == 0 && sgn(a.y - b.y) == 0; } inline double ptDis(Point a, Point b)//点间距 { return sqrt(sqr(a.x - b.x) + sqr(a.y - b.y)); } inline double dotDet(Vec a, Vec b)//点乘 { return a.x * b.x + a.y * b.y; } inline double crossDet(Vec a, Vec b)//叉乘 { return a.x * b.y - a.y * b.x; } inline double crossDet(Point o, Point a, Point b)//向量叉乘 { return crossDet(a - o, b - o); } inline bool onSeg(Point x, Point a, Point b)//判断点在线段ab上 { return sgn(crossDet(a - x, b - x)) == 0 && sgn(dotDet(a - x, b - x)) < 0||x==a||x==b; } int segIntersect(Point a, Point c, Point b, Point d)//线段相交判断,返回2是一条线段一端在另一线段上 { Vec v1 = b - a, v2 = c - b, v3 = d - c, v4 = a - d; int a_bc = sgn(crossDet(v1, v2)); int b_cd = sgn(crossDet(v2, v3)); int c_da = sgn(crossDet(v3, v4)); int d_ab = sgn(crossDet(v4, v1)); if(a_bc *c_da > 0 && b_cd *d_ab > 0) return 1; if(onSeg(b, a, c) && c_da) return 2; if(onSeg(c, b, d) && d_ab) return 2; if(onSeg(d, c, a) && a_bc) return 2; if(onSeg(a, d, b) && b_cd) return 2; return 0; } int main() { #ifdef DeBUGs freopen("//home//amb//桌面//1.in","r",stdin); #endif int T; scanf("%d",&T); double XS,YS,XT,YT,XA,YA,XB,YB,XC,YC; while(T--) { scanf("%lf%lf%lf%lf%lf%lf%lf%lf%lf%lf",&XS,&YS,&XT,&YT,&XA,&YA,&XB,&YB,&XC,&YC); if(fabs(XS-XT)<EPS && fabs(YS-YT)<EPS) { printf("0.000000 "); continue; } double distance=INF; Point s(XS,YS); Point t(XT,YT); Point a(XA,YA); Point b(XB,YB); Point c(XC,YC); if(segIntersect(s,t,a,b)!=1&&segIntersect(s,t,b,c)!=1&&!onSeg(b,s,t)) { distance=min(distance,ptDis(s,t)); } if(segIntersect(s,a,b,c)!=1&&segIntersect(a,t,b,c)!=1) { distance=min(distance,ptDis(s,a)+ptDis(a,t)); } if(segIntersect(s,c,a,b)!=1&&segIntersect(c,t,a,b)!=1) { distance=min(distance,ptDis(s,c)+ptDis(c,t)); } if(segIntersect(s,b,a,c)!=1&&segIntersect(b,t,a,c)!=1) { if((crossDet(s,b,a)*crossDet(s,b,c)>=0&& crossDet(t,b,a)*crossDet(t,b,c)>=0)||onSeg(a,s,b)|| onSeg(c,s,b)||onSeg(a,b,t)||onSeg(c,b,t)) distance=min(distance,ptDis(s,b)+ptDis(b,t)); } if(segIntersect(s,a,b,c)!=1) distance=min(distance,ptDis(s,a)+ptDis(a,b)+ptDis(b,t)); if(segIntersect(s,c,b,a)!=1) distance=min(distance,ptDis(s,c)+ptDis(c,b)+ptDis(b,t)); if(segIntersect(t,a,b,c)!=1) distance=min(distance,ptDis(t,a)+ptDis(a,b)+ptDis(b,s)); if(segIntersect(t,c,a,b)!=1) distance=min(distance,ptDis(t,c)+ptDis(c,b)+ptDis(b,s)); if(segIntersect(s,c,a,b)!=1) distance=min(distance,ptDis(s,c)+ptDis(c,a)+ptDis(a,t)); if(segIntersect(s,a,b,c)!=1) distance=min(distance,ptDis(s,a)+ptDis(c,a)+ptDis(c,t)); printf("%.6lf ",distance); } return 0; }
Pakhom and the Gully
Time Limit : 2000/1000ms (Java/Other) Memory Limit : 131072/65536K (Java/Other)
Total Submission(s) : 44 Accepted Submission(s) : 4
Problem Description
Pakhom stands at the point S and wants to reach the point T to buy the land there. But he noticed a gully, which represents a polyline ABC. What is the length of the shortest path Pakhom should walk if he doesn't want to fall into the gully?
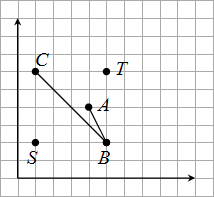
Input
The first line contains the number of testcases n (1 ≤ n ≤ 5000). Each of the next n lines contains one testcase. Each testcase is written as 10 space-separated integers: xS, yS, xT, yT, xA, yA, xB, yB, xC, yC, the coordinates of the points S, T, A, B, and C, respectively. All points within the test case are different. Points S and T don't belong to the polyline ABC. All numbers in test cases don't exceed 10 by absolute value.
Input
The first line contains the number of testcases n (1 ≤ n ≤ 5000). Each of the next n lines contains one testcase. Each testcase is written as 10 space-separated integers: xS, yS, xT, yT, xA, yA, xB, yB, xC, yC, the coordinates of the points S, T, A, B, and C, respectively. All points within the test case are different. Points S and T don't belong to the polyline ABC. All numbers in test cases don't exceed 10 by absolute value.
Output
For each test case output the answer on a separate line. The answer should be precise up to 10−6.
Sample Input
| input | output |
|---|---|
3 1 2 5 6 4 4 5 2 1 6 2 2 4 3 1 3 3 3 3 1 2 1 4 4 3 2 4 3 1 4 |
8.000000 3.650282 3.828427 |
Author
Petr Lezhankin
Source
Ufa SATU Contest. Petrozavodsk Summer Session, August 2009
坑爹啊,看着很简单,枚举情况多的吓人,各种想不到加坑爹才过了这题
