快速排序（交换排序）-八大排序汇总（6）

基本思想　

　　1．先从数列中取出一个数作为基准数。

　　2．分区过程，将比这个数大的数全放到它的右边，小于或等于它的数全放到它的左边。

　　3．再对左右区间重复第二步，直到各区间只有一个数。

性能

　　时间复杂度：平均情况下的时间复杂度为O(nlogn)。最坏情况下时间复杂度为O(n²)。

　　空间复杂度：除去程序运行实现的空间消费（例如递归栈），快速排序算法只需消耗确定数量的空间（即O(1)，常数级空间）。

　　稳定性：不稳定的算法

注意

　　编译器函数库自带的快速排序函数：qsort()

　　用 法: void qsort(void *base, int nelem, int width, int (*fcmp)(const void *,const void *)); 　　

　　各参数：1 待排序数组首地址 2 数组中待排序元素数量 3 各元素的占用空间大小 4 指向函数的指针

代码及分析

快速排序的第一种写法

　　方法一：以第一个元素为基准，哨兵j从后往前找比基准元素大的数的位置，哨兵i从前往后找比基准元素小的数的位置，将两个位置的元素交换。。。直到哨兵i和哨兵j相遇，相遇位置的元素与基准元素交换。这时相遇位置左边的元素都比基准元素大，右边的元素都比基准元素小。将两边的元素各作为一个序列进行递归操作。

　　http://developer.51cto.com/art/201403/430986.htm

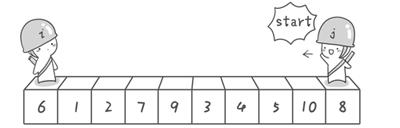
　　初始序列“6  1  2 7  9  3  4  5 10  8”

　　先从右往左找一个小于6的数，再从左往右找一个大于6的数，然后交换他们。这里可以用两个变量i和j，分别指向序列最左边和最右边。我们为这两个变量起个好听的名字“哨兵i”和“哨兵j”。刚开始的时候让哨兵i指向序列的最左边（即i=1），指向数字6。让哨兵j指向序列的最右边（即=10），指向数字8。

　　首先哨兵j开始出动。因为此处设置的基准数是最左边的数，所以需要让哨兵j先出动，这一点非常重要。哨兵j一步一步地向左挪动（即j--），直到找到一个小于6的数停下来。接下来哨兵i再一步一步向右挪动（即i++），直到找到一个数大于6的数停下来。最后哨兵j停在了数字5面前，哨兵i停在了数字7面前。

现在交换哨兵i和哨兵j所指向的元素的值。交换之后的序列如下：

6  1  2  5  9 3  4  7  10  8

　　到此，第一次交换结束。接下来开始哨兵j继续向左挪动（再友情提醒，每次必须是哨兵j先出发）。他发现了4（比基准数6要小，满足要求）之后停了下来。哨兵i也继续向右挪动的，他发现了9（比基准数6要大，满足要求）之后停了下来。此时再次进行交换，交换之后的序列如下：

6  1  2 5  4  3  9  7 10  8

　　

　　第二次交换结束，“探测”继续。哨兵j继续向左挪动，他发现了3（比基准数6要小，满足要求）之后又停了下来。哨兵i继续向右移动，糟啦！此时哨兵i和哨兵j相遇了，哨兵i和哨兵j都走到3面前。说明此时“探测”结束。我们将基准数6和3进行交换。交换之后的序列如下：

3  1 2  5  4  6  9 7  10  8

　　

　　到此第一轮“探测”真正结束。此时以基准数6为分界点，6左边的数都小于等于6，6右边的数都大于等于6，接下来只要模拟刚才的方法分别处理6左边和右边的序列即可。回顾一下刚才的过程，其实哨兵j的使命就是要找小于基准数的数，而哨兵i的使命就是要找大于基准数的数，直到i和j碰头为止。

　　整个过程如下图所示：

代码如下：

void quicksort1(int a[],int left, int right)
{
    int i, j, t, temp;
    if (left>right)
        return;

    temp = a[left]; //temp中存的就是基准数 
    i = left;
    j = right;
    while (i < j) // while (i != j)
    {
        //顺序很重要，要先从右边开始找 
        while (a[j] >= temp && i<j)
            j--;
        //再找右边的 
        while (a[i] <= temp && i<j)
            i++;
        //交换两个数在数组中的位置 
        if (i<j)
        {
            swap(a[i],a[j]);
        }
    }
    //最终将基准数归位,下面两句可用swap(a[left], a[i]);代替
    a[left] = a[i];
    a[i] = temp;

    quicksort1(a,left, i - 1);//继续处理左边的，这里是一个递归的过程 
    quicksort1(a,i + 1, right);//继续处理右边的 ，这里是一个递归的过程 
}

int _tmain(int argc, _TCHAR* argv[])
{
    int a[] = { 12, 34, 21, 55, 27, 32, 33, 53, 22, 14, 4, 2, 6, 9 };
    quicksort1(a, 0, 13);

    for (int m = 0; m < 14; m++)
    {
        cout << a[m] << ",";
    }
    cout << endl;

    system("pause");
    return 0;
}

快速排序的第二种写法

　　方法二（挖坑）：以第一个元素为基准，先挖出来，哨兵j从后往前找比基准大的数的位置，找到后将该位置元素填进基准挖好的坑内，这时j位置留下一个坑；哨兵i从前往后找比基准元素小的数的位置，将该位置的元素挖出来填进j留下的坑中，这时i位置留下一个坑；j继续往前查找。。。直到哨兵i和哨兵j相遇，将基准元素填进相遇位置的“坑”内。这时相遇位置左边的元素都比基准元素大，右边的元素都比基准元素小。将两边的元素各作为一个序列进行递归操作。

//快速排序
void quicksort2(int s[], int l, int r)
{
    if (l < r)
    {
        //Swap(s[l], s[(l + r) / 2]); //将中间的这个数和第一个数交换 参见注1
        int i = l, j = r, x = s[l];
        while (i < j)
        {
            while (i < j && s[j] >= x) // 从右向左找第一个小于x的数
                j--;
            if (i < j)
                s[i++] = s[j];

            while (i < j && s[i] < x) // 从左向右找第一个大于等于x的数
                i++;
            if (i < j)
                s[j--] = s[i];
        }
        s[i] = x;
        quicksort2(s, l, i - 1); // 递归调用 
        quicksort2(s, i + 1, r);
    }
}

int _tmain(int argc, _TCHAR* argv[])
{
    int a[] = { 12, 34, 21, 55, 27, 32, 33, 53, 22, 14, 4, 2, 6, 9 };
    quicksort2(a, 0, 13);

    for (int m = 0; m < 14; m++)
    {
        cout << a[m] << ",";
    }
    cout << endl;

    system("pause");
    return 0;
}

　　快速排序还有很多改进版本，如随机选择基准数，区间内数据较少时直接用另的方法排序以减小递归深度。