(Description)
给定p,
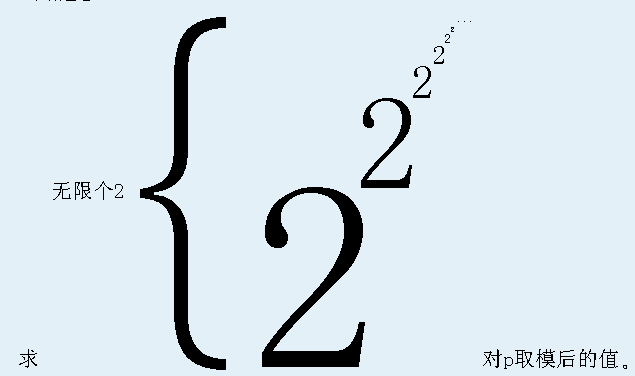
(Solution)
欧拉定理:(若(a,p)=1),则(a^bequiv a^{b\%varphi(p)}(mod p)).
扩展欧拉定理:(a^bequiv a^{b\%varphi(p)+varphi(p)}(mod p)) (a为任意整数,b,p为正整数,且(b>varphi(p))(a,p不一定要互质).证明.
指数是无穷的,但是模数是有限的,从不断减小p去考虑。
设(f(p)=2^{2^{2^{...}}}mod p),次数是无穷的,所以肯定(>p)。根据扩展欧拉定理可得
[egin{aligned} f(p)&=2^{2^{2^{...}}mod varphi(p)+varphi(p)}(mod p)\&=2^{f(varphi(p))+varphi(p)}(mod p)end{aligned}
]
这样就有了f的递推式,可以直接递归计算。
那么复杂度是多少?
若(p)为偶数,则(varphi(p)leqfrac{p}{2});若(p)为奇数,则(varphi(p))为偶数,转化为偶数的情况。所以最多递归(log_2p)层。
(n>2时,varphi(n)始终为偶数)的一个证明:
设(n=prod p_i^{a_i}),则(varphi(n)=prod (p_i^{a_i}-p_i^{a_i-1})).
若(n=2^a,ageq 2),则(varphi(n)=2^a-2^{a-1}=2^{a-1}(2-1)),为偶数。
否则,若(n>2),且至少有一个奇素数p,则(p_a-p_{a-1}(ageq 1))为偶数(因为两个数都是奇数)。
另官方题解.
#include<cstdio>
#include<cstring>
typedef long long LL;
const int N=1e7+3,M=10005;
int p,val[N],P[M+3],cnt;
bool NP[M+3];
void Init()
{
for(int i=2;i<M;++i)
{
if(!NP[i]) P[++cnt]=i;
for(int j=1;j<=cnt&&i*P[j]<M;++j)
{
NP[i*P[j]]=1;
if(!(i%P[j])) break;
}
}
}
int FP(LL x,int k,LL p)
{
LL t=1;
for(;k;k>>=1,x=x*x%p)
if(k&1) t=t*x%p;
return t;
}
int Get_Phi(int n)//O(sqrt(n))求单值欧拉函数
{
LL res=1;int mod=n;
for(int t,i=1;i<=cnt&&P[i]*P[i]<=n;++i)
if(!(n%P[i]))
{
n/=P[i], (res*=(P[i]-1))%=mod;
while(!(n%P[i])) n/=P[i],(res*=P[i])%=mod;
}
if(n>1) (res*=n-1)%=mod;//别忘n本身可能是个质数
return res;
}
int Calc(int n)
{
if(val[n]!=-1) return val[n];
int t=Get_Phi(n);
return val[n]=FP(2,Calc(t)+t,n);
}
int main()
{
Init();
int t; memset(val,0xff,sizeof val), val[1]=0;
for(scanf("%d",&t);t--;)
{
scanf("%d",&p);
printf("%d
",Calc(p));
}
return 0;
}