2018.10.4 正睿国庆集训测试 青岛
时间:3.5h
期望得分:100+10+30
实际得分:100+10+30
果然我不适合半夜做题 看了这么长时间这道题还写了这么长时间。。=-=

A 陈太阳与序列(单调队列)
写了四遍_(xз」∠)_。。前两遍的树状数组和单调队列因为a[i]=seed%(r-l+1)+l写成a[i]=seed%(r-l+1)+1死活不过大样例直接重写了。
第三遍因为手写双端队列就是过不了大样例不知道为什么。。
然后做了2.5h。
用两个单调队列维护前面的最大最小值可以(O(n))做(一个队列也可以吧)。这样空间也是(O(n))的。
注意到数据是随机生成的,一个元素在队列中存在时间的期望为(frac{1}{n-i+1})(后面存在比它大/小的元素就出队了)。
所以队列大小只需要(sumfrac 1i=O(log n))就够了。为了方便可以用deque。
//zbl
#include <queue>
#include <cstdio>
#include <algorithm>
#define mod 1000000007
#define mp std::make_pair
#define pr std::pair<int,int>
typedef long long LL;
const int N=1e6+2;
std::deque<pr> q1,q2;
int main()
{
// freopen("ex_A2.in","r",stdin);
// freopen(".out","w",stdout);
int n,K,seed,l,r; scanf("%d%d%d%d%d",&n,&K,&seed,&l,&r);
int tmp=seed,len=r-l+1;
LL ans=0;
for(int i=1,p=0,ai; i<=n; ++i)
{
ai = seed%len+l;
seed=(13331ll*seed+23333)%mod;
while(!q1.empty() && ai>q1.back().first) q1.pop_back();
while(!q2.empty() && ai<q2.back().first) q2.pop_back();
q1.push_back(mp(ai,i)), q2.push_back(mp(ai,i));
while(!q1.empty() && !q2.empty() && q1.front().first>1ll*K*q2.front().first)
{
if(q1.front().second<q2.front().second) p=q1.front().second, q1.pop_front();
else p=q2.front().second, q2.pop_front();
}
if(!q1.empty() && !q2.empty()) ans+=i-p;
}
printf("%lld
",ans);
return 0;
}
B 陈太阳与直径(树的计数 DP 卡常)
Description:(n)个节点有标号的无根树,直径为(0,1,…,n−1)的树有多少个。
先考虑(n)个点的有标号生成树怎么计数。
令(f[n])表示(n)个点的有根树的数量。假设确定根的标号,设除根节点外标号最小的节点所在的子树的大小为(k)(考虑最小标号可以避免重复计数)。
那么(f[n]=n imessum_{k=1}^{n-1}f[k] imesfrac{f[n-k]}{n-k} imes C_{n-2}^{k-1})。
(frac{1}{n-k})即,把(n-k)个点的树,根的标号选择方案先除掉(由该树合并上(k)那棵子树)。
(C_{n-2}^{k-1})即确定根节点标号,且另一个最小标号也确定,从(n-2)个标号中选(k-1)个给(k)的子树((n-k-1)给另一棵子树)。
最后再乘(n)即根的标号的选择方案。
由上面树的计数,再知道两棵树的最大深度及直径后,我们就可以合并直径了。
令(f[i][j][k])表示(i)个点,子树最大深度为(j),直径为(k),的方案数。
那么(6)个for枚举。(f[n][max(d_1+1,d_2)][max(l_1,l_2,d_1+d_2+1)]=n imessum_k f[k][d1][l1] imesfrac{f[n-k][d2][l2]}{n-k} imes C_{n-2}^{k-1})
复杂度(O(n^6))。
计算直径不超过(k)的树的个数。
令(f[i][j])表示(i)个点,最大深度为(j)的方案数。
在外层枚举(k)。转移要满足(d_1+d_2+1leq k)。
(f[n][max(d_1+1,d_2)]=n imessum_k f[k][d1] imesfrac{f[n-k][d2]}{n-k} imes C_{n-2}^{k-1})
复杂度(O(n^5))。可以用前缀和优化到(O(n^4))。
每棵树都有唯一的中心。
如果直径为偶数,那么中心是一个点,否则中心是一条边。
如果中心是一个点,那么中心两旁最大深度的子树至少出现了两次;
否则,直径为奇数,要求合并的两棵子树深度相同。
这样好像就可以得到答案了?
令(f[i][j])表示(i)个点,深度至多为(j)的方案数。
令(g[i][j])表示(i)个点,深度恰好为(j)的方案数。
那么
(f[n][i]=n imessum_kf[k][i-1] imesfrac{f[n-k][i]}{n-k} imes C_{n-2}^{k-1})
(g[n][i]=f[n][i]-f[n][i-1])。
统计答案:
直径为奇数时(设为(2l+1)),枚举直径一边子树大小,同样 令除根外标号最小的点在被合并的子树中。这样根随意确定,根确定后标号最小的点也确定。即方案有(C_{n-1}^{k-1})种。
即答案为(sum_kg[k][l] imes g[n-k][l] imes C_{n-1}^{k-1})。
如图(这图应该在上面就有吧==):
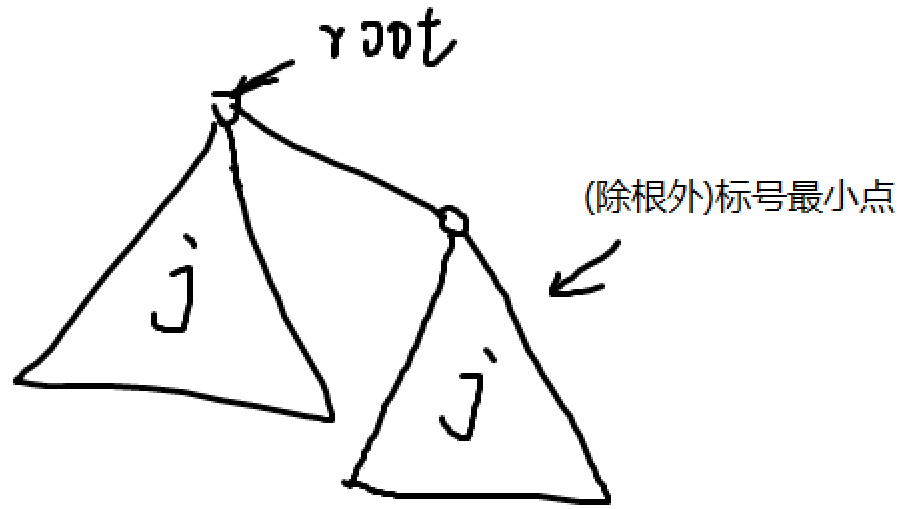
直径为偶数时(设为(2l)),那么答案为有至少两棵深度为(l)的子树的树的方案数。
(g[l][n])会有不合法情况(最大深度子树只出现了一次)。减掉从(g[l-1][n])转移到(g[l][n])时的值就行了(从(l-1)转移到的(l),最大深度(l)只出现一次)
(即用最大深度为(l)的所有方案,减去某棵最大深度不足(l)的树并上某棵最大深度为(l-1)的树,得到最大深度为(l)的树的方案数)
因为被并上的子树是唯一的(它深度最大((l-1))),所以不需要去重,直接分配标号即可(系数为(C_n^k))。
唯一是指,如图,若(A)子树深度也为(l-1),那么直接分配标号即可。否则(A)子树深度(<l-1),肯定不会和(B)相同。

那么答案为(sum_kg[k][l-1] imes f[n-k][l-1] imes C_{n}^{k})。
代码实现:
因为直接做常数有点大,只有90分。所以要卡卡常。
组合数要(n^2)预处理。直接用阶乘(O(1))算还要两次取模。
注意到这个转移(最大深度为第一维,点数为第二维):f[i][j]=j*Σf[i-1][k]*f[i][j-k]*inv[j-k]*C[j-2][k-1]可以写成f[i][j]=j*fac[j-2]*Σ(f[i-1][k]*ifac[k-1])*(f[i][j-k]*ifac[j-k-1]*inv[j-k])。
我们可以存两个辅助数组f2[i][j]=f[i][j]*ifac[j-1],f3[i][j]=f[i][j]*ifac[j-1]*inv[j],这样可以有效减少取模次数。
//132ms 5448kb
#include <cstdio>
#define Mod(x) x>=mod&&(x-=mod)
typedef long long LL;
const int N=504;
const LL Lim=6e18;
int f[N][N],f2[N][N],f3[N][N],g[N][N],inv[N],C[N][N],fac[N],ifac[N];
inline int FP(int x,int k,int mod)
{
int t=1;
for(; k; k>>=1,x=1ll*x*x%mod)
if(k&1) t=1ll*t*x%mod;
return t;
}
//#define C(n,m,mod) 1ll*fac[(n)]*ifac[(m)]%mod*ifac[(n)-(m)]%mod
int main()
{
int n,mod; scanf("%d%d",&n,&mod);
inv[1]=fac[0]=fac[1]=1;
for(int i=2; i<=n; ++i) inv[i]=1ll*(mod-mod/i)*inv[mod%i]%mod, fac[i]=1ll*fac[i-1]*i%mod;
ifac[n]=FP(fac[n],mod-2,mod);
for(int i=n-1; ~i; --i) ifac[i]=1ll*ifac[i+1]*(i+1)%mod;
C[0][0]=1;
for(int i=1; i<=n; ++i)
{
C[i][0]=1, C[i][i]=1;
for(int j=1; j<i; ++j)
C[i][j]=C[i-1][j-1]+C[i-1][j], Mod(C[i][j]);
}
f[0][1]=1, f2[0][1]=1, f3[0][1]=1, g[0][1]=1;
for(int i=1; i<n; ++i)//mxdep
{//f[i][j]:深度至多为i,j个点的方案数
int *F=f[i],*F2=f2[i],*F22=f2[i-1],*F3=f3[i];
F[1]=1, F2[1]=1, F3[1]=1;
for(int j=2; j<=n; ++j)//n (num of vertices)
{
LL tmp=0;
for(int k=1; k<j; ++k)
{
tmp+=1ll*F22[k]*F3[j-k];
if(tmp>=Lim) tmp%=mod;
// tmp+=1ll*f[i-1][k]*F[j-k]%mod*inv[j-k]%mod*C[j-2][k-1]%mod;
// fac[j-2]*ifac[k-1]*ifac[j-k-1]
}
tmp%=mod;
F[j]=1ll*j*tmp%mod*fac[j-2]%mod;
F2[j]=1ll*F[j]*ifac[j-1]%mod;
F3[j]=1ll*F2[j]*inv[j]%mod;
}
for(int j=1; j<=n; ++j) g[i][j]=F[j]-f[i-1][j];//-
}
for(int i=0; i<n; ++i)
{
if(!i) {printf("%d ",n==1); continue;}
LL ans=0; int l=i>>1;
if(i&1)
for(int j=1; j<n; ++j)
ans+=1ll*g[l][j]*g[l][n-j]%mod*C[n-1][j-1]%mod;
else
{
ans=g[l][n];
for(int j=1; j<n; ++j)
ans+=mod-1ll*g[l-1][j]*f[l-1][n-j]%mod*C[n][j]%mod;
}
printf("%d ",(int)((ans%mod+mod)%mod));
}
return 0;
}
C 陈太阳与酒店(分数规划 DP 线段树)
容易看出只要(k)至少为(2)就没有用了。没人住的酒店是合法的当且仅当每个点不是孤立点且它是独立集(之间没有边)。
分数规划,二分答案(x),求是否存在方案满足(sum (a[i]-x)geq0)。
把每个酒店的权值改为(a[i]-x)。这样我们应尽量不选负权值点(即把它们作为没人住的酒店),它需要是独立集。那么我们可以求一个权值和最小的独立集。
负数且求最小权值和很奇怪,反正不妨把权值写成(x-a[i]),求权值最大的独立集。
(二分图最大权独立集=总权值-最小割)。这样线段树优化建图跑网络流可以得到(60)分。
把所有权值都与(0)取个(max)。这样就不需要单独考虑负权的了。
考虑对二分图的右侧(右边酒店)DP。令(f[i])表示到右侧第(i)家酒店且选(i)的最大权值。我们枚举一个(f[j](j<i))转移,即(j+1sim i-1)都不选,这样连边区间完全在(j+1sim i-1)的左侧的点都能选择。
直接枚举是(O(n^3log v))的。
可以用前缀和预处理完全包含在区间([l,r])内的所有权值和(s[l][r])。把区间按右端点排序。枚举左端点,然后移动右端点算就行了。
这样就是(O(n^2log v))了。
考虑每个区间([l,r])的贡献(w)(其实就是个点权),当(j<l,r<i)时,(f[i]=max{f[j]+w}),即有(w)这个贡献。可以想到区间加。那么线段树维护区间最大值、单点修改、区间加就好了。
复杂度(O(nlog nlog v))。
//2046ms 48260kb
#include <cstdio>
#include <cctype>
#include <algorithm>
//#define gc() getchar()
#define MAXIN 200000
#define gc() (SS==TT&&(TT=(SS=IN)+fread(IN,1,MAXIN,stdin),SS==TT)?EOF:*SS++)
#define eps 1e-8
typedef long long LL;
const int N=3e4+5;
int n,m,A[N],B[N],Enum,H[N],nxt[N],to[N],id[N];
char IN[MAXIN],*SS=IN,*TT=IN;
struct Segment_Tree
{
#define ls rt<<1
#define rs rt<<1|1
#define lson l,m,ls
#define rson m+1,r,rs
#define S N<<2
double mx[S],add[S];
#undef S
#define Upd(rt,v) mx[rt]+=v,add[rt]+=v
#define Update(rt) mx[rt]=std::max(mx[ls],mx[rs])
inline void PushDown(int rt)
{
Upd(ls,add[rt]), Upd(rs,add[rt]), add[rt]=0;
}
void Modify(int l,int r,int rt,int p,double v)
{
if(l==r) {mx[rt]=v; return;}
if(add[rt]>eps) PushDown(rt);
int m=l+r>>1;
if(p<=m) Modify(lson,p,v);
else Modify(rson,p,v);
Update(rt);
}
void Add(int l,int r,int rt,int R,double v)
{
if(r<=R) {Upd(rt,v); return;}
if(add[rt]>eps) PushDown(rt);
int m=l+r>>1;
Add(lson,R,v);
if(m<R) Add(rson,R,v);
Update(rt);
}
double Query(int l,int r,int rt,int R)
{
if(r<=R) return mx[rt];
if(add[rt]>eps) PushDown(rt);
int m=l+r>>1;
if(m<R) return std::max(Query(lson,R),Query(rson,R));
else return Query(lson,R);
}
}T[45];
inline int read()
{
int now=0;register char c=gc();
for(;!isdigit(c);c=gc());
for(;isdigit(c);now=now*10+c-'0',c=gc());
return now;
}
inline void AE(int u,int v,int ID)//r->l
{
to[++Enum]=v, nxt[Enum]=H[u], H[u]=Enum, id[Enum]=ID;
}
bool Check(double x)
{
static double wa[N],wb[N];
static int Time=-1;
++Time;
double sum=0,f;
for(int i=1; i<=n; ++i) sum+=A[i]-x, wa[i]=std::max(0.0,x-A[i]);
for(int i=1; i<=m; ++i) sum+=B[i]-x, wb[i]=std::max(0.0,x-B[i]);
#define S 0,m,1//m
for(int i=1; i<=m; ++i)
{
f=T[Time].Query(S,i-1)+wb[i];
T[Time].Modify(S,i,f);
for(int j=H[i]; j; j=nxt[j])
T[Time].Add(S,to[j]-1,wa[id[j]]);
}
return sum+T[Time].Query(S,m)>0;//
#undef S
}
int main()
{
n=read(),m=read(),read();
for(int i=1; i<=n; ++i) A[i]=read();
for(int i=1; i<=m; ++i) B[i]=read();
for(int i=1; i<=n; ++i) AE(read(),read(),i);
double l=0,r=1e5,mid;
while(l+eps<r)
if(Check(mid=(l+r)*0.5)) l=mid;
else r=mid;
printf("%.8lf
",l);
return 0;
}
考试代码
B
#include <set>
#include <cstdio>
#include <cctype>
#include <cstring>
#include <algorithm>
#define gc() getchar()
typedef long long LL;
const int N=21;
int n,mod,A[N],vis[N],Ans[N],Enum,H[N],nxt[N<<1],to[N<<1],dis[N];
bool used[N];
#define AE(u,v) to[++Enum]=v, nxt[Enum]=H[u], H[u]=Enum, to[++Enum]=u, nxt[Enum]=H[v], H[v]=Enum
int BFS(int s)
{
static const int N=505;
static int q[N],pre[N];
int h=0,t=1;
q[0]=s, dis[s]=pre[s]=0;
while(h<t)
{
int x=q[h++];
for(int i=H[x],v; i; i=nxt[i])
if((v=to[i])!=pre[x])
// printf("%d->%d
",x,v),
dis[v]=dis[x]+1, pre[v]=x, q[t++]=v;
}
return q[t];
}
int Calc()
{
int s=BFS(1),t=BFS(s);
// printf("%d
",dis[t]);
return dis[t];
}
void Check()
{
static int cnt[N];
memcpy(cnt,vis,sizeof cnt);
std::set<int> st;
for(int i=1; i<=n; ++i) if(!cnt[i]) st.insert(i);
Enum=0, memset(H,0,sizeof H), memset(used,0,sizeof used);
for(int i=3; i<=n; ++i)
{
int v=*st.begin(), u=A[i];
AE(u,v), used[v]=1, st.erase(v);
if(!--cnt[u] && !used[u]) st.insert(u);
}
int u=*st.begin(), v=*st.rbegin();
AE(u,v);
++Ans[Calc()];
}
void DFS(int x)
{
if(x>n)
{
Check();
return;
}
for(int i=1; i<=n; ++i)
++vis[i], A[x]=i, DFS(x+1), --vis[i];
}
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
scanf("%d%d",&n,&mod);
if(n==5) printf("0 0 5 60 60");
if(n==4) printf("0 0 4 12");
if(n==3) printf("0 0 3");
if(n==2) printf("0 1");
if(n==1) printf("1");
if(n<=5) return 0;
DFS(3);
for(int i=0; i<n; ++i) printf("%d ",Ans[i]);
return 0;
}
C
#include <cstdio>
#include <cctype>
#include <algorithm>
#define gc() getchar()
typedef long long LL;
const int N=6e4+5;
int n,m,K,A[N],Enum,H[N],nxt[N],to[N];
bool tag[N];
double Ans;
inline int read()
{
int now=0;register char c=gc();
for(;!isdigit(c);c=gc());
for(;isdigit(c);now=now*10+c-'0',c=gc());
return now;
}
inline void AE(int u,int v)
{
// to[++Enum]=v, nxt[Enum]=H[u], H[u]=Enum;
to[++Enum]=u, nxt[Enum]=H[v], H[v]=Enum;
}
bool Check2(int x)
{
for(int i=H[x]; i; i=nxt[i])
if(tag[to[i]]) return 0;
return 1;
}
//bool Check()
//{
// static int q[N],cost[N],vis[N],Time=0;
// ++Time;
// int h=0,t=0;
// for(int i=1; i<=n; ++i) if(tag[i]) q[t++]=i, cost[i]=K, vis[i]=Time;
// while(h<t)
// {
// int x=q[h++];
// for(int i=H[x],v; i; i=nxt[i])
// if(vis[v=to[i]]==Time)
// if()
// }
// return 1;
//}
void DFS(int x,int sum,int tot)
{
if(x>n+m)
{
if(tot) Ans=std::max(Ans,(double)sum/tot);
return;
}
DFS(x+1,sum+A[x],tot+1);
if(Check2(x)) tag[x]=1, DFS(x+1,sum,tot), tag[x]=0;
}
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
n=read(), m=read(), K=read();
for(int i=1; i<=n; ++i) A[i]=read();
for(int i=1; i<=m; ++i) A[i+n]=read();
for(int i=1; i<=n; ++i)
for(int l=read(),r=read(); l<=r; ++l) AE(i,l+n);
DFS(1,0,0), printf("%.8lf
",Ans);
return 0;
}
