2018.10.23 正睿停课训练 Day7
期望得分:100+?+40
实际得分:100+20+40
A 矩形(组合)
#include <cstdio>
#include <cctype>
#include <algorithm>
#define gc() getchar()
#define mod 1000000007
typedef long long LL;
const int N=2e5+5;
int fac[N],ifac[N];
inline int read()
{
int now=0;register char c=gc();
for(;!isdigit(c);c=gc());
for(;isdigit(c);now=now*10+c-'0',c=gc());
return now;
}
inline int FP(int x,int k)
{
int t=1;
for(; k; k>>=1,x=1ll*x*x%mod)
if(k&1) t=1ll*t*x%mod;
return t;
}
inline int C(int n,int m)
{
if(n<0||m<0) return 0;
return 1ll*fac[n+m]*ifac[n]%mod*ifac[m]%mod;
}
int main()
{
int n=read(),m=read(),A=read(),B=read(),lim=n+m;
fac[0]=fac[1]=1;
for(int i=2; i<=lim; ++i) fac[i]=1ll*fac[i-1]*i%mod;
ifac[lim]=FP(fac[lim],mod-2);
for(int i=lim; i; --i) ifac[i-1]=1ll*ifac[i]*i%mod;
LL ans=0;
if(B!=m-1)
{
for(int i=1; i<n-A; ++i)
ans+=1ll*C(m-B-2,n-i)*C(B,i-1)%mod;
ans+=1ll*C(m-B-1,A)*C(B,n-A-1)%mod;
}
else ans+=1ll*C(m-B-1,A)*C(B,n-A-1)%mod;
printf("%lld
",ans%mod);
return 0;
}
B 翻转(思路)
(A)左移/右移等价于(B)右移/左移。考虑移动(B)。
(B)显然不会反复左移右移。假设(B)左移了(a)次,然后右移(a+b)次,那么(B)中每个(1)就覆盖了区间([-a,b])。
我们先枚举最终状态,也就是(A[1])最终对应了哪个(B[i])。
先令(B)左移(i-1)次。那对于此时(A)和(B)仍不相同的位置((A^{wedge}B)中(1)的位置),必须被(B)中的某个(1)覆盖。
枚举(a),再(O(n))扫一遍就可以得到此时的答案(min{2a+b})。这样就是(O(n^3))的做法。
对每个(A,B)不同的位置(p),记(L(p))表示若左移(B)来覆盖(p)最少还需要多少次左移(就是(p)到右边最近的(1)的距离)("还需要"是指左移(i)次后),(R(p))表示若右移(B)来覆盖(p)最少需要多少次右移。
那么对于每个(p),要么满足(ageq L(p)),要么(bgeq R(p))。
把所有的限制按(L)排序,从大到小枚举(a),(b)要满足的限制就是(R)的后缀最大值。
因为(a)最多到(n-1),对每个(a)求一个最大的(R),然后从大到小枚举即可,可以不排序。(排序也不影响复杂度,还更方便。。)(代码是枚举的(b))
复杂度(O(n^2))。
这样枚举的是左移多少,然后算需要右移多少位。还需要枚举右移多少位。把(A,B reverse)再这样求一遍即可。
//269ms 540kb
#include <cstdio>
#include <cctype>
#include <cstring>
#include <algorithm>
#define gc() getchar()
typedef long long LL;
const int N=4005,INF=2e9;
char A[N],B[N];
int Solve(int n)
{
static int L[N],R[N],mxR[N];
for(int i=1; i<=n; ++i) B[i+n]=B[i];
for(L[1]=0; B[n-L[1]+1]=='0'; ++L[1]);
for(int i=2; i<=n; ++i) L[i]=B[i]=='1'?0:L[i-1]+1;
for(R[n]=0; B[n+R[n]]=='0'; ++R[n]);
for(int i=n-1; i; --i) R[i]=B[i]=='1'?0:R[i+1]+1;
int ans=1e9;
for(int i=0; i<n; ++i)
{
int cnt=0;
memset(mxR,0,sizeof mxR);
for(int j=1; j<=n; ++j)
if(A[j]!=B[i+j]) ++cnt, mxR[L[j]]=std::max(mxR[L[j]],R[j]-i);//<<i 右移L[j]次时,除左移i次外还需左移mxR[L[j]]次
for(int j=n-1,mx=0; ~j; --j)
ans=std::min(ans,2*j+2*mx+i+cnt), mx=std::max(mx,mxR[j]);
}
return ans;
}
int main()
{
scanf("%s%s",A+1,B+1); int n=strlen(A+1),f=0;
for(int i=1; i<=n; ++i) if(B[i]=='1') {f=1; break;}
if(!f)
{
for(int i=1; i<=n; ++i) if(A[i]=='1') return puts("-1"),0;
return puts("0"),0;
}
int ans=Solve(n);
std::reverse(A+1,A+1+n), std::reverse(B+1,B+1+n);
ans=std::min(ans,Solve(n));
printf("%d
",ans);
return 0;
}
C 求和(思路 三元环计数)
(k=1)时,每条边都会在(2^{n-2})种方案中出现,直接输出(m*2^{n-2})即可。
(k=2)时,令(g(i)=[边i是否存在(i的两个端点都在s中)]),则(Ans=sum_{所有方案}left(sum_{i=1}^mg(i)
ight)^2=sum_{所有方案}left(sum_{i=1}^mg(i)*sum_{i=1}^mg(i)
ight))。
(sum_{i=1}^mg(i)*sum_{i=1}^mg(i))就是(sum_{i=1}^msum_{j=1}^mg(i)*g(j))((i)可以等于(j)),即枚举两条边,如果它们同时存在,则贡献为(1)。
那么答案就是任意两条边(e_1,e_2)同时存在的方案数((e_1)可以等于(e_2))。
我们枚举每一条边(e_1),再看一下第二条边(e_2)选哪条以及在多少个集合里即可。有三种情况:
(e_1=e_2):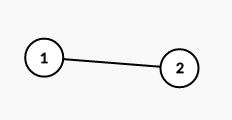
(e_1,e_2)有一个公共端点: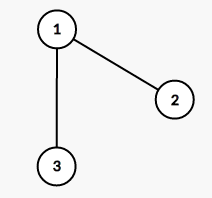
(e_1,e_2)无公共端点:
每种情况对应有多少条边((e_2))可以用度数算,且都确定了一些点必须选。设必须选(x)个点,则乘上(2^{n-x})的系数即可。
复杂度(O(m))。
(k=3)时,同样,计算三条边同时存在的方案数。
如果只枚举一条边,情况太多且系数不好判断。但是我们可以直接枚举三条边,然后算这三条边一共确定了哪几个点必须选(sort,unique即可),设有(x)个,则这三条边的贡献为(2^{n-x})。
这样复杂度(O(m^3))。结合暴力+上面的算法,期望得分(80)。
满分做法:
有心情再写。。?
太神了。。自己造些数据然后高斯消元求系数?
80分代码:
#include <cstdio>
#include <cctype>
#include <vector>
#include <algorithm>
#define gc() getchar()
#define MAXIN 300000
//#define gc() (SS==TT&&(TT=(SS=IN)+fread(IN,1,MAXIN,stdin),SS==TT)?EOF:*SS++)
#define mod 1000000007
#define Mod(x) x>=mod&&(x-=mod)
typedef long long LL;
const int N=1e5+5;
int A[N],B[N],dgr[N],pw[N];
char IN[MAXIN],*SS=IN,*TT=IN;
inline int read()
{
int now=0;register char c=gc();
for(;!isdigit(c);c=gc());
for(;isdigit(c);now=now*10+c-'0',c=gc());
return now;
}
int main()
{
int n=read(),m=read(),K=read(); pw[0]=1;
for(int i=1; i<=n; ++i) pw[i]=pw[i-1]<<1, Mod(pw[i]);
for(int i=1; i<=m; ++i) ++dgr[A[i]=read()], ++dgr[B[i]=read()];
if(K==1) return printf("%lld
",1ll*m*pw[n-2]%mod),0;
if(K==2)
{
LL ans=1ll*m*pw[n-2]%mod;//e1=e2
for(int i=1,d1,d2; i<=m; ++i)
{
d1=dgr[A[i]], d2=dgr[B[i]];
if(n>=3) ans+=1ll*(d1+d2-2)*pw[n-3]%mod;
if(n>=4) ans+=1ll*(m-d1-d2+1)*pw[n-4]%mod;
}
return printf("%lld
",ans%mod),0;
}
if(K==3)
{
LL ans=0;
for(int i=1; i<=m; ++i)
for(int j=1; j<=m; ++j)
for(int k=1; k<=m; ++k)
{
int a[6]={A[i],B[i],A[j],B[j],A[k],B[k]},t;
std::sort(a,a+6), t=std::unique(a,a+6)-a;
ans+=pw[n-t];
}
return printf("%lld
",ans%mod),0;
}
return 0;
}
考试代码
B1
xjbDP。。
#include <cstdio>
#include <cctype>
#include <cstring>
#include <algorithm>
#define gc() getchar()
typedef long long LL;
const int N=4005,INF=2e9;
int n,pre[N],nxt[N],f[N][2],g[N][2];
bool ok[N];
char A[N],B[N];
bool Check()
{
for(int i=1; i<=n; ++i) if(A[i]!=B[i]) return 0;
return 1;
}
bool Check2()
{
for(int i=1; i<=n; ++i) if(A[i]=='1') return 0;
return 1;
}
inline int Calc(int l,int r)
{
if(l<=r) return r-l;
return n-r+l;
}
int Solve1(int x)
{
int ans=x-1+(B[1]!=A[x]);//to left x-1
f[x][0]=0, f[x][1]=INF, g[x][0]=x-1, g[x][1]=0;
for(int i=x+1; i<x+n; ++i)
{
f[i][0]=f[i-1][0], f[i][1]=f[i-1][1];
g[i][0]=g[i-1][0], g[i][1]=g[i-1][1];
if(A[i]==B[i-x+1]) continue;
if(A[i]=='0'&&B[i-x+1]=='1') {++ans; continue;}
++ans;
int p=i>n?i-n:i;
int tmp=std::max(Calc(pre[p],i)-g[i-1][0],0);
f[i][0]=std::min(f[i-1][0]+tmp,f[i-1][1]+2*tmp);
g[i][0]=std::max(g[i][0],Calc(pre[p],i));
tmp=std::max(Calc(i,nxt[p])-g[i-1][1],0);
f[i][1]=std::min(f[i-1][1]+tmp,f[i-1][0]+2*tmp);
g[i][1]=std::max(g[i][1],Calc(i,nxt[p]));
}
// printf("To left %d:%d
",x-1,ans+std::min(f[x+n-1][0],f[x+n-1][1]));
return ans+std::min(f[x+n-1][0],f[x+n-1][1]);
}
int Solve2(int x)
{
int ans=n-x+1+(B[1]!=A[x]);//to right n-(x-1)
f[x][0]=INF, f[x][1]=0, g[x][0]=0, g[x][1]=n-x+1;
for(int i=x+1; i<x+n; ++i)
{
f[i][0]=f[i-1][0], f[i][1]=f[i-1][1];
g[i][0]=g[i-1][0], g[i][1]=g[i-1][1];
if(A[i]==B[i-x+1]) continue;
if(A[i]=='0'&&B[i-x+1]=='1') {++ans; continue;}
++ans;
int p=i>n?i-n:i;
int tmp=std::max(Calc(pre[p],i)-g[i-1][0],0);
f[i][0]=std::min(f[i-1][0]+tmp,f[i-1][1]+2*tmp);
g[i][0]=std::max(g[i][0],Calc(pre[p],i));
tmp=std::max(Calc(i,nxt[p])-g[i-1][1],0);
f[i][1]=std::min(f[i-1][1]+tmp,f[i-1][0]+2*tmp);
g[i][1]=std::max(g[i][1],Calc(i,nxt[p]));
}
return ans+std::min(f[x+n-1][0],f[x+n-1][1]);
}/*
1010
1100
11010
10001
0101101010
1001010001
1101010010
010110110
100101001
*/
int main()
{
scanf("%s%s",A+1,B+1), n=strlen(A+1);
for(int i=1; i<=n; ++i) if(B[i]=='1') ok[i]=1;
if(Check()) return puts("0"),0;
int p=0;
for(int i=1; i<=n; ++i) if(ok[i]) {p=i; break;}
if(!p&&!Check2()) return puts("-1"),0;
nxt[n+1]=p;
for(int i=n; i; --i) nxt[i]=ok[i]?i:nxt[i+1];
p=0;
for(int i=n; i; --i) if(ok[i]) {p=i; break;}
pre[0]=p;
for(int i=1; i<=n; ++i) pre[i]=ok[i]?i:pre[i-1];
for(int i=1; i<=n; ++i) A[i+n]=A[i];
int ans=INF;
for(int i=1; i<=n; ++i) ans=std::min(ans,std::min(Solve1(i),Solve2(i)));
printf("%d
",ans==INF?-1:ans);
return 0;
}
B2
#include <cstdio>
#include <cctype>
#include <bitset>
#include <cstring>
#include <algorithm>
typedef long long LL;
const int N=4005,INF=2e9;
int n;
char s[N];
std::bitset<2005> a,b,f,g,g1,tmp;
void to_left()
{
int flag=g[0];
g>>=1;
if(flag) g.set(n-1);
}
void to_right()
{
int flag=g[n-1];
g<<=1;
g.reset(n);
if(flag) g.set(0);
}
int work_R(int x)
{
int now=0;
for(int i=1; i<=x; ++i)
{
to_right();
tmp=g&b;
now+=tmp.count();
g^=tmp;
}
return now;
}
int work_L(int x)
{
int now=0;
for(int i=1; i<=x; ++i)
{
to_left();
tmp=g&b;
now+=tmp.count();
g^=tmp;
}
return now;
}
void Solve()
{
int ans=1e9,cnt;
for(int i=0; i<n; ++i) if(a[i]!=b[i]) f.set(i);
tmp=f&b;
cnt=tmp.count();
f^=tmp;
for(int t1,t2,i=0; i<=n; ++i)
{
g=f;
t1=work_R(i);
g1=g;
for(int j=0; j<=n; ++j)
{
g=g1;
t2=work_L(i+j);
if(!g.count()) ans=std::min(ans,cnt+t1+t2+i+(i+j)+j);
}
}
for(int t1,t2,i=0; i<=n; ++i)
{
g=f;
t1=work_L(i);
g1=g;
for(int j=0; j<=n; ++j)
{
g=g1;
t2=work_R(i+j);
if(!g.count()) ans=std::min(ans,cnt+t1+t2+i+(i+j)+j);
}
}
for(int i=1; i<n; ++i)
{
f.reset();
for(int j=0; j<n; ++j)
{
int k=(j+i) % n;
if(a[k]!=b[j]) f.set(k);
}
tmp=f&b;
cnt=tmp.count();
f^=tmp;
for(int j=0,t1,t2; j<=i; ++j)
{
g=f;
t1=work_R(j);
t2=work_L(i+j);
if(!g.count()) ans=std::min(ans,cnt+t1+t2+j+(i+j));
}
for(int j=0,t1,t2; j<=(n-i-1); ++j)
{
g=f;
t1=work_L(j);
t2=work_R(n-(i-j));
if(!g.count()) ans=std::min(ans,cnt+t1+t2+j+(n-(i-j)));
}
}
printf("%d
",ans);
}
int main()
{
scanf("%s",s+1);
n=strlen(s+1);
for(int i=1; i<=n; ++i) if(s[i]=='1') a.set(i-1);
scanf("%s",s+1);
for(int i=1; i<=n; ++i) if(s[i]=='1') b.set(i-1);
Solve();
return 0;
}
C
#include <cstdio>
#include <cctype>
#include <algorithm>
#define gc() getchar()
#define MAXIN 300000
//#define gc() (SS==TT&&(TT=(SS=IN)+fread(IN,1,MAXIN,stdin),SS==TT)?EOF:*SS++)
#define mod 1000000007
#define Mod(x) x>=mod&&(x-=mod)
typedef long long LL;
const int N=1e5+5;
int n,m,K,Enum,H[N],nxt[N<<1],to[N<<1],dgr[N];
char IN[MAXIN],*SS=IN,*TT=IN;
inline int read()
{
int now=0;register char c=gc();
for(;!isdigit(c);c=gc());
for(;isdigit(c);now=now*10+c-'0',c=gc());
return now;
}
inline void AE(int u,int v)
{
++dgr[v], to[++Enum]=v, nxt[Enum]=H[u], H[u]=Enum;
++dgr[u], to[++Enum]=u, nxt[Enum]=H[v], H[v]=Enum;
}
namespace Subtask1
{
const int N=20;
int n,m,K;
LL Ans;
bool chose[N],mp[N][N];
void DFS(int x)
{
if(x>n)
{
int ans=0;
for(int i=1; i<=n; ++i)
if(chose[i])
for(int j=i+1; j<=n; ++j)
if(chose[j]&&mp[i][j]) ++ans;
int tmp=ans;
for(int k=1; k<K; ++k) ans=1ll*ans*tmp%mod;
Ans+=ans;
return;
}
chose[x]=0, DFS(x+1), chose[x]=1, DFS(x+1);
}
void Main()
{
n=::n,m=::m,K=::K;
for(int i=1,u,v; i<=m; ++i) u=read(),v=read(),mp[u][v]=mp[v][u]=1;
DFS(1), printf("%lld
",Ans%mod);
}
}
int main()
{
Enum=1,n=read(),m=read(),K=read();
if(n<=17) return Subtask1::Main(),0;
for(int i=1; i<=m; ++i) AE(read(),read());
if(K==1)
{
int pw2=1;
for(int i=1; i<=n-2; ++i) pw2<<=1, Mod(pw2);
printf("%lld
",1ll*m*pw2%mod);
return 0;
}
return 0;
}