2020牛客暑期多校训练营（第二场）Greater and Greater

题目链接

https://ac.nowcoder.com/acm/contest/5667/G

题目大意

给你一个长度为 N 的数组 A 和一个长度为 M 的数组 B

问 A 中存在多少个长度为 M 的子串使得 Ai >= B1 , Ai+1 >= B2 , ... , Ai+m >= Bm

解题思路

样例为 N = 6 , M = 3 ,  A = { 1,4,2,8,5,7} , B = {2,3,3}

我们对每个 Bj 求一个长度为 N 的 bitset ，设为Bis [ j ]

其意义为 若 Ai 大于等于 Bj , 则 Bis[ pos[ Ai ] ] = 1 , 否则为 0

那么对应样例我们得到的 Bis 分别为

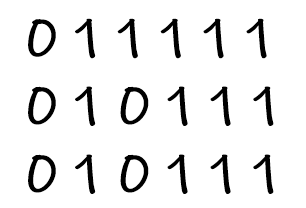
容易发现若存在这么一条右斜线 , 可以从 1 走到 m , 则 ans ++

我们将第 J 个 Bis[j] 左移 J - 1位 , 得到

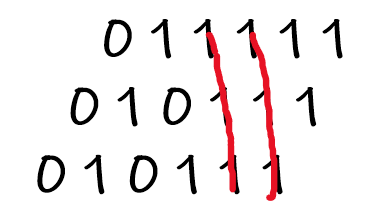
于是原来的斜线就变成了竖线

那么我们只要把所有的 Bis[j] 左移之后进行 & 运算 , 然后统计最后的结果有多少 1 即可

那么 Bis [j] 怎么求呢？

我们可以先对 A , B 进行降序排序 , 然后执行下图操作(画的有点丑hh)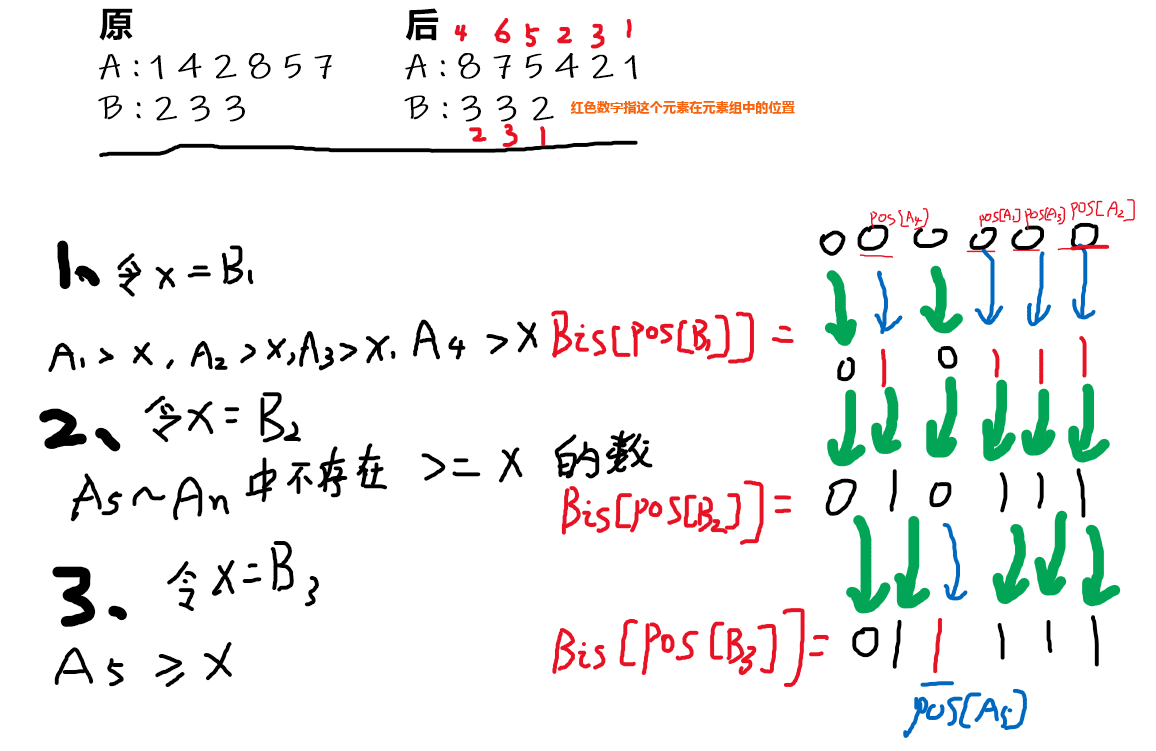

AC_Code

#include<bits/stdc++.h>
#define fi first
#define se second
using namespace std;
const int N = 2e5 + 10;
pair<int , int>a[N] , b[N];
bitset<N>ans , now;
signed main()
{
    ios::sync_with_stdio(false) , cin.tie(0) , cout.tie(0);
    int n , m ;
    cin >> n >> m ;
    for(int i = 1 ; i <= n ; i ++) cin >> a[i].fi , a[i].se = i;
    for(int i = 1 ; i <= m ; i ++) cin >> b[i].fi , b[i].se = i;
    sort(a + 1 , a + 1 + n , greater<pair<int , int>>());
    sort(b + 1 , b + 1 + m , greater<pair<int , int>>());
    ans.set() , now.reset();
    int pos = 1;
    for(int i = 1 ; i <= m ; i ++)
    {
        while(pos <= n && a[pos].fi >= b[i].fi) now.set(a[pos].se) , pos ++ ;
        ans &= now >> b[i].se; 
    }
    cout << ans.count() << '
';
    return 0;
}