3. 用MATLAB优化工具箱的测试

线性规划

题目： 

 

 第0问  如何安排生产使利润最大

假设生产甲饮料x百箱，乙饮料y百箱，利润为z

  

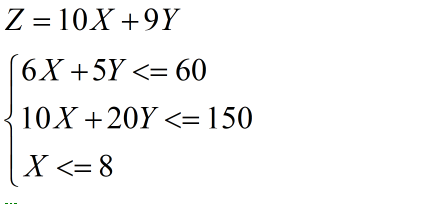
 上代码

c=[-10 -9];%因为linprog找的是最小值，所以这个地方取相反数。
% <=条件约束
A=[6 5; 10 20];
b=[60; 150];
%  =条件约束
Aeq=[];
beq=[];
%变量范围约束
vlb=[0,0];
vub=[];
[x,fval]=linprog(c,A,b,Aeq,beq,vlb,vub); 

运行结果

x =

    6.4286

    4.2857 

fval =

 -102.8571

 当X =642 Y = 428 时候大概取最优值（是不是X应该多一个或者Y少一个，我懒得算了,正式比赛再说）

此时利润 Z = 102.72

 

第1问  若投资0.8万元可增加原料1千克,问应否作这项投资.

假设生产甲饮料x百箱，乙饮料y百箱，利润为z，增加了W千克

 

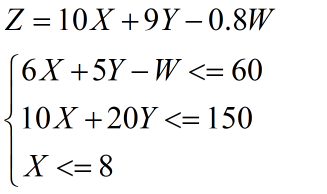
 代码

c=[-10 -9 0.8];%因为linprog找的是最小值，所以这个地方取相反数。
% <=条件约束
A=[6 5 -1; 10 20 0];
b=[60; 150];
%  =条件约束
Aeq=[];
beq=[];
%变量范围约束
vlb=[0,0,0];
vub=[8,1000,1000];   %1000视为无穷大，表示没有限制
[x,fval]=linprog(c,A,b,Aeq,beq,vlb,vub); 

结果

x =

    8.0000

    3.5000

    5.5000

fval =

 -107.1000

所以要投资5.5千克比较好

第2问  若每百箱甲饮料获利可增加1万元,问应否改变生产计划。

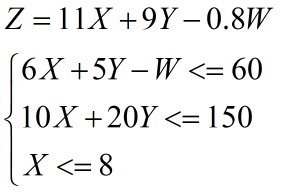
代码

c=[-11 -9 0.8];%因为linprog找的是最小值，所以这个地方取相反数。
% <=条件约束
A=[6 5 -1; 10 20 0];
b=[60; 150];
%  =条件约束
Aeq=[];
beq=[];
%变量范围约束
vlb=[0,0,0];
vub=[8,1000,1000];   %1000视为无穷大，表示没有限制
[x,fval]=linprog(c,A,b,Aeq,beq,vlb,vub); 

结果

x = 

    8.0000

    3.5000

    5.5000 

fval = 

 -115.1000 

由此可得不需要改变策略。

非线性规划 

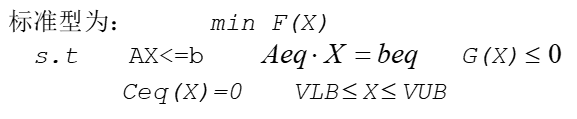
 1.首先建立M文件fun.m,定义目标函数F(x):

function f= =fun (X) ;

f= =F(X) ;

 2.   若约束条件中有非线性约束:G(X)或Ceq(X)=0,则建立M文件nonlcon.m定义函数G(X)与Ceq(X):

function [G,Ceq]=nonlcon(X)

G=...

Ceq=...

 3.建立主程序.非线性规划求解的函数是fmincon,命令的基本格式如下:

(1)x=fmincon( 'fun' ,Xo,A,b)

(2) x=fmincon( 'fun' ,Xo,A,b, Aeq, beq)

(3) x=fmincon( 'fun' ,Xo,A,b, Aeq, beq, VLB, VUB)

(4) x=fmincon( 'fun' ,Xo,A,b, Aeq, beq, VLB, VUB, ' nonlcon' )

(5)x-fmincon( 'fun' ,Xo,A,b, Aeq, beq, VLB, VUB, 'nonlcon' ,options)

(6) [x, fval]= fmincon(...)

(7) [x, fval,exitflag]= fmincon(...) 

(8) [x, fval, exi tflag, output]= fmincon(.. .)

非线性案例

案例1

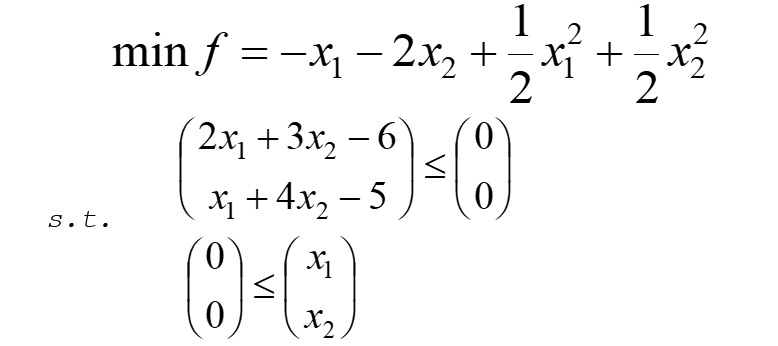
 代码：

fun.m

function f=fun(x);
f=-x(1)-2*x(2)+(1/2)*x(1)^2+(1/2)*x(2)^2

main.m

x0=[1;1];
A=[2 3 ;1 4]; b=[6;5];
Aeq=[];beq=[];
VLB=[0;0]; VUB=[];
[x,fval]=fmincon('fun',x0,A,b,Aeq,beq,VLB,VUB)

结果

x = 

    0.7647

    1.0588

fval =

   -2.0294

案例二

 

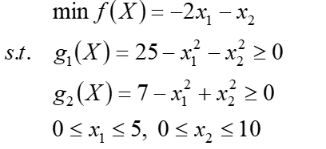
 fun.m

function f=fun(x);
f=-2*x(1)-x(2);

mycon.m

function [g,ceq]=mycon(x)
g=[x(1)^2+x(2)^2-25;x(1)^2-x(2)^2-7];
ceq = [];

main.m

x0=[3;2.5];
A=[];b=[];
Aeq=[];beq=[];
vlb=[0 0];vub=[5 10];
[x,fval]=fmincon('fun',x0,A,b,Aeq,beq,vlb,vub,'mycon')

解得结果是

x =

    4.0000

    3.0000

fval =

  -11.0000

一元函数求极值

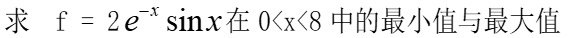
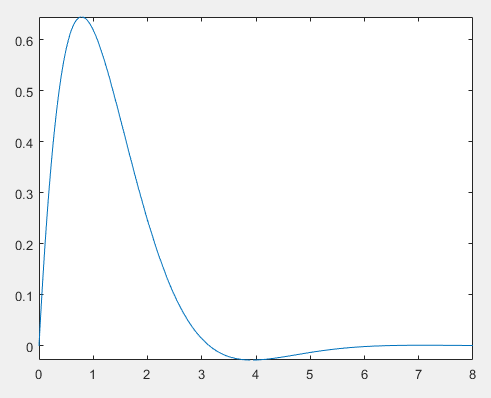
f= '2*exp(-x).*sin(x)' ; 
%找最小值
fplot(f,[0,8]); %作图语句
[miny_X,miny_Y]=fminbnd (f, 0,8); %找最小y的横纵坐标 
%找的最大值
f1='-2*exp(-x).*sin(x)';
[maxy_X,maxy_Y]=fminbnd (f1, 0,8) 

 

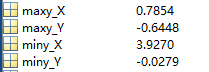
 多元函数无约束优化

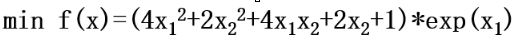
main.m

x0 = [-1, 1];
x=fminunc('fun',x0);
y=fun(x)

fun.m

function f = fun (x)
f = exp(x(1))*(4*x(1)^2+2*x(2)^2 +4*x(1)*x(2)+2*x(2)+1);

 结果：

x =

0.5000 -1.0000 

y =

3.6609e-15

二次规划

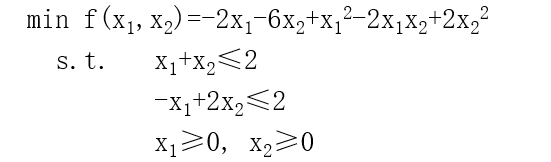
写成标准式:

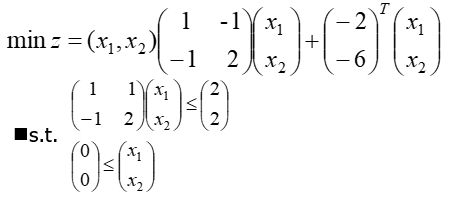
 代码

H=[1 -1; -1 2]; 
c=[-2 ;-6];A=[1 1; -1 2];b=[2;2];
Aeq=[];beq=[]; VLB=[0;0];VUB=[];
[x,z]=quadprog(H,c,A,b,Aeq,beq,VLB,VUB)

结果

x =0.6667
1.3333
z = -8.2222