Github项目地址:
https://github.com/SwallowQAQ/caculate
psp 表格
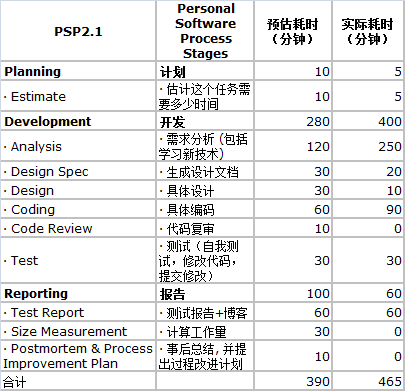
解题思路:
首先明确四则运算是先乘除后加减,如果有括号,先计算括号内的,再计算括号外的。一道四则运算的算式不一定有四种符号,一般指由两个或两个以上运算符号及括号,把多数合并成一个数的运算。
所以要考虑的问题有:是否要生成括号,生成几个运算符,计算数值的范围,计算结果不能为负数,除数不能为0。
这道题中,为了便于测试,我设定数值范围是0到20的数字,如果需要可以修改,考虑题目里可能会出现分数的情况,可以设定计算几道题和可以设定运算符数量,时间问题,这次的题目中未考虑括号。
函数设计:
函数主要分成三个,主函数main(),随机生成表达式expression(n),计算表达式js(s)。
获取用户需要的设定通过主函数完成,包括循环生成表达式和计算得分,生成表达式是通过列表保留每个数字和运算符,再转换成字符串显示给用户,在将这个列表通过计算表达式的函数将列表转换成可用eval()函数直接计算的字符串。
代码说明:
from fractions import * import random def main():#主函数 print('输入题目的数量:') n = int(input()) print('输入运算符的数量(建议2或3):') fn = int(input()) print("本次共 {} 题,满分 100 分".format(n)) flag=0 for i in range(n): while 1: ex = expression(fn) an=eval(js(ex)) s=str(an) if '.' in s: continue if an>=0: if '/'in s: if an >1: continue a=''.join(ex) print(a) if eval(input())==an: flag+=1 print('回答正确!') else: print("回答错误!,正确答案是{}".format(an)) break print("共答对{}题,本次得分:{}".format(flag,round(100/n*flag))) def expression(n):#生成表达式 f = ['+','-','*','÷','/'] fl = [] ex = [] pren = 0 pre = '' for i in range(n+1): if pre == '÷': pren = random.randint(1, 20) pre = f[random.randint(0, 2)] elif pre == '/': pren = random.randint(1, 20) pre = f[random.randint(0, 2)] ex.append(str(pren)) ex.append(pre) pren = random.randint(1, 20) pre = f[random.randint(0, 2)] else: pren = random.randint(1, 20) pre = f[random.randint(0, 4)] ex.append(str(pren)) ex.append(pre) ex[-1] = '=' return ex def js(s):#返回可计算字符串 f = ['+', '-', '*', '÷', '/'] l=len(s) jg='' for i in range(0,int(l/2)-1): if s[2*i+1] in f[:4]: if i==0: jg=jg+s[0] if s[2*i+3] =='/': if s[2*i+1] =='÷': jg = jg + '/' else: jg=jg+s[2*i+1] else: if s[2*i+1] =='÷': jg = jg + '/'+ s[2*i+2] else: jg = jg +s[2*i+1]+ s[2*i+2] else: jg=jg+'Fraction('+s[2*i]+','+s[2*i+2]+')' return str(jg) main()
运行结果:

说明:/是表示分子和分母的分割线,÷才是表示除法。
代码测试:
expression(n)函数主要是生成表达式,因此不能直接测试,但生成的表达式需要进行修改成可计算的表达式,因此两个函数都是不能直接测试的,但是可以测试生成的表达式经过修改是否可以直接计算,如果出现修改后的表达式为(2+3)2,这种情况用eval是会出错的,在写代码时候我是有一边测试的,一些基本的错误改过来了,现在写一个测试代码,测试1w个例子,代码如下:
def test(): for i in range(10000): ex=expression(2) a=js(ex) b=eval(a)
运行结果:

也就是表明表达式都是可以计算的,每道题是否合法是用主函数控制的,当结果是负数或者为假分数或者为小数的时候,重新生成表达式。
其实这样的代码是有一些问题的,比如我测试的时候发现有3-8+8这样的例子,计算结果不为负数,但是其实算不合法的,因为按顺序计算3-8已经出现负数了,因此该加入一个新的函数,用于测试可计算的表达式是否合法,以及将表达式计算结果是否合理也放在该函数中判断,再返回合理的表达式。这时主函数也应修改,修改代码不作展示。
性能分析:
性能分析使用pycharm中提供的profile工具测试,如下图
思路:在当前代码下,点击proifle这个工具的时候,是和普通的运行函数一样的,但是当程序结束会附带一个分析表,而测试结果和设定的题目数量等有关系,如果按照一般的流程,等待用户输入的时间应该是最大的,这里我将函数代码修改一下,将问题数量设为10000,运算符为2,将需要用户输入的地方修改成100。
运行结果如下

也就是说这10000道题中有147道题的结果为100,具体是哪些就不看了,接下来看看性能统计表,如下所示
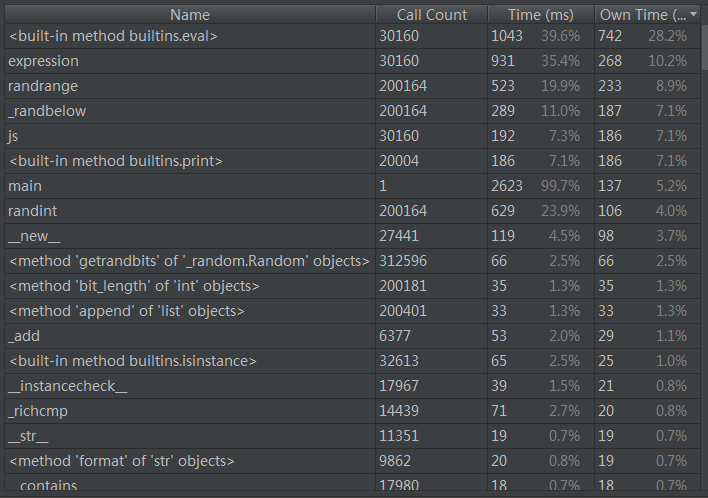
由表可以看出,eval和expression和js函数都调用了30160次,也就是每次生成一个表达式时候都需要做一次计算,并且可以知道大约生成3次表达式,才有一条的计算结果是符合要求的。
看到调用次数最多的是生成随机数的函数,这个和运算符数量还有式子个数有关,最少要生成((2*运算符数量+1)*式子数量),但这里直接跟调用expression函数有关。
js这个函数花的时间是较少的,但eval和expression两个函数都花比较多的时间,eval是不可避免的,每一个式子都必须要计算一次,才能得出结果,因此可以考虑修改一下expression函数,让他的返回结果是合法的。降低调用expression函数的次数,eval的次数也减少,总时间就会减少了。
个人总结
知识总结:
- Fraction()-->完成分数的表示和计算,并且用分数表示出来。
- eval()-->可以自动进行四则混合运算(带括号),但是本次题目没有加入括号运算
- 代码测试-->可以发现程序隐藏的错误。
- 性能测试-->能够很方便地看到程序的运行时间及效率,对于以后的修改可以更加专业且有针对性。
个人感悟:
题目看起来很简单,但是分析起来会发现有特别多的情况,如果只是随机生成数字运算会比较简单,结果有要求又会变得麻烦一些,加上括号可能更复杂,个人练习比较少,写个不是很复杂的代码也花很长时间,又加上对各种函数不熟悉,做起来更慢,需要多练习才行。以后有机会再将这个四则运算功能写更完善一些。