树的直径详解

树的直径，又称树的最长链，定义为一棵树上最远的两个节点的路径，即树上一条不重复经过某一条边的最长的路径。树的直径也可以代指这条路径的长度。

求树的直径有两种比较常用的方法：树形DP和搜索，时间复杂度均为$O(n)$。接下来会对两种方法都进行讲解。

在接下来的实现中，树是以邻接表存无向边的形式给出的。

---

树形DP

设$d_x$表示从$x$走向以其为根的子树，能够到达的最远距离。再设$x$的$k$个子节点分别为$s_1,s_2,...,s_k$。显然可以得出关于$d$数组的转移方程：

for(int i=1;i<=k;i++)
    d[x]=max(d[x],d[s[i]]+dist(x,s[i]));

其中$dist_{i,j}$表示$i,j$之间的距离。这个转移方程很好得出，请读者自己思考。

设$l_x$表示经过$x$的最长链的长度，$dr$表示该树的直径，若该树有$n$个节点，则有：

for(int i=1;i<=n;i++)
    dr=max(dr,l[i]);

那么如何推出$l$数组呢？对于$x$的任意两个子节点$s_u,s_v$，经过这三个节点的最长链显然为$d_{s_u}+dist_{s_u,x}+dist_{x,s_v}+d_{s_v}$。于是有以下的状态转移方程：

for(int i=1;i<=k;i++)
    for(int j=1;j<i;j++)
        l[x]=max(l[x],d[s[i]]+dist(s[i],x)+dist(x,s[j])+d[s[j]]);

因为$dr$就是所有$l_x$中的最大值，所以可以不必再多定义一个$l$数组，直接定义一个整形变量$ans$存储答案，每次直接更新就可以了。

这个状态转移方程还可以进一步优化。实际上，在运行时，对于任意两个点$u,v(v<u)$（这里假设循环时按编号从小到大的顺序遍历，即先遍历$v$，再遍历$u$），在循环到$u$时，根据$d_x$的转移方程，此时$d_x$内已经存储了编号小于$i$的所有$x$的子节点$v$的最大的$d_{s_v}+dist_{s_v,x}$。换句话说，就是实现了下面这个步骤：

for(int j=1;j<i;j++)
    d[x]=max(d[x],d[s[j]]+dist(s[j],x));

因此，我们可以省去这一步，直接先用$d_x$来代替$max(d_{s_v}+dist(s_v,x))$来更新$l
_x$，省去了一层循环，实现优化。注意，在这里一定要先更新$l_x$，再更新$d_x$，这里的正确性请读者自己思考。

还有一点，为了避免往回走，要开一个访问数组来标记是否已访问。这是遍历的基本要求，就不赘述了。

这样整体实现步骤就非常清晰了，如果有地方没看懂的可以结合下面的代码一起思考。

树形DP求树的直径代码：

void tree_dp(int now)
{
    v[now]=1;//维护访问数组
    for(int i=head[now];i;i=Next[i])
    {
        int y=ver[i];
        if(v[y])
            continue;//已访问过则不再访问
        tree_dp(y);
        ans=max(ans,d[now]+d[y]+edge[i]);//先更新l[x]
        d[now]=max(d[now],d[y]+edge[i]);//再更新d[x]
    }
}

---

搜索

通过两次搜索可以求出树的直径，同时还能求出具体路径。这里的搜索用DFS和BFS均可。

搜索求树的直径需要两步：

1. 任选一节点$s$，搜索找到距离$s$最远的节点$x$；
2. 再搜索一遍，找到距离$x$最远的节点$y$。$dist_{x,y}$就是树的直径

为什么$dist_{x,y}$就是树的直径呢？因为第1步时找到离$s$最远的节点$x$，此时$x$一定是直径的一个端点；而第2步找到离$x$最远的节点$y$，$y$一定是直径的另一个端点。这两步都是可以证明的。

下面给出本人自己的拙劣的证法，若有不严谨之处请见谅。

1、证明 xx 一定是直径的一个端点

证明：

假设直径的两个端点为 u,vu,v 且 u,v eq xu,v≠x ，路径 (u,v)(u,v) 和路径 (u,x)(u,x) 交于节点 oo ，则有以下三种情况：

1. 路径$(u,v)$经过$s$
2. 路径$(u,v)$不经过$s$且路径$(o,x)$经过$s$
3. 路径$(u,v)$不经过$s$且路径$(o,x)$不经过$s$

根据定义，显然有$dist_{s,v}<dist_{s,x}$。

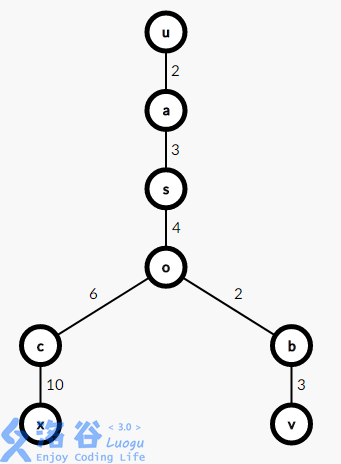
对于第一种情况，有$dist_{u,v}=dist_{u,s}+dist_{s,v}<dist_{u,s}+dist_{s,x}=dist_{u,x}$，与直径的定义矛盾。

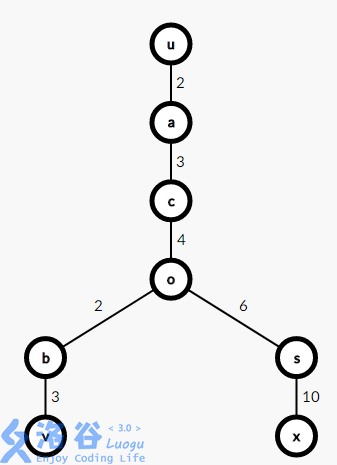
对于第二种情况，有$dist_{u,v}=dist_{u,o}+dist_{o,v}=dist_{u,o}+dist_{s,v}-dist_{s,o}<dist_{u,o}+dist_{s,x}+dist_{s,o}=dist_{u,o}+dist_{o,x}=dist_{u,x}$，与直径的定义矛盾。

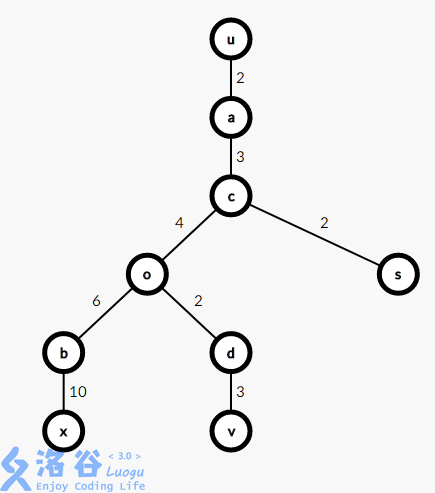
对于第三种情况，有$dist_{u,v}=dist_{u,o}+dist_{o,v}=dist_{u,o}+dist_{s,v}-dist_{s,o}<dist_{u,o}+dist_{s,x}-dist_{s,o}=dist_{u,o}+dist_{o,x}=dist_{u,x}$，与直径的定义矛盾。

因为三种情况都不成立，$x$一定是直径的一个端点。

证毕。

2、证明$y$一定是直径的另一个端点**

证明：

假设直径的另一个端点为$e$且$e eq y$，根据定义$dist_{x,e}<dist_{x,y}$，与直径的定义矛盾，因此$y$一定是直径的另一个端点。

证毕。

搜索实现起来当然很简单了！这里就不赘述了，直接奉上代码。

搜索求树的直径代码：

void dfs(int now,int cnt)
{
    bool ok=false;
    v[now]=1;
    for(int i=head[now];i;i=Next[i])
    {
        int y=ver[i];
        if(v[y])
            continue;
        ok=true;
        dfs(y,cnt+edge[i]);
    }
    if(!ok && cnt>ans)
    {
        ans=cnt;
        ansid=now;
    }
}

---

习题：

• 简单应用题：P4408
• 综合应用题：P4381

---

2019.6.28 于厦门外国语学校石狮分校