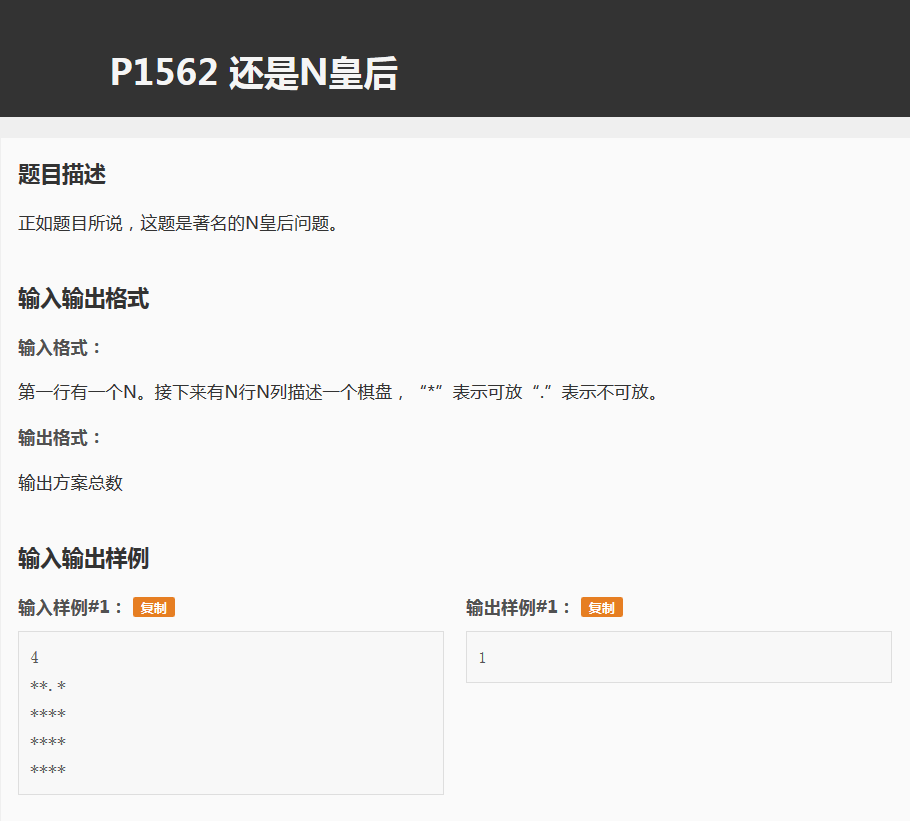
先看题才是最重要的:
这道题有点难理解,毕竟Code speaks louder than words,所以先亮代码后说话:
1 #include<iostream> 2 using namespace std; 3 char s[1000];int n,map[1000],mod,ans; 4 void dfs(int deep,int line,int lr,int rl) 5 { 6 if(deep>n) 7 { 8 ans++; 9 return; 10 } 11 int pos=mod&(~(line|lr|rl|map[deep])),p; 12 while(pos) 13 { 14 p=pos&-pos; 15 pos-=p; 16 dfs(deep+1,line+p,(lr+p)<<1,(rl+p)>>1); 17 } 18 } 19 int main() 20 { 21 cin>>n; 22 mod=(1<<n)-1; 23 for(int i=1;i<=n;i++) 24 { 25 cin>>s; 26 for(int j=0;j<n;j++) 27 map[i]=(s[j]=='.')+(map[i]<<1); 28 } 29 dfs(1,0,0,0); 30 cout<<ans; 31 return 0; 32 }
这道题是一道搜索+二进制优化题,其实是八皇后的升级版,这就说明你的前置要求是要回普通的八皇后(不会点这里),初见此题,小编便鼓起勇气,without thinking twice就稍加改动提交了一遍原来八皇后的代码,结果甚是残忍。
就算是开O2优化也没有用,亲测无效。那么就只能换个思路了,怎样能快一些呢?我们不禁会联想到二进制和位运算(推荐隔壁Alan_Anders的博客二进制和位运算符,小编懒得再多写一篇这样的博客了),我们可以尝试把这个问题简单化,只考虑最根本的问题:我们通常判断一个格子是否可以放置皇后,需要哪些要素呢?这就很显然了,只要懂国际象棋规则的,就一定知道只要这个位置没有被其他皇后攻击到就可以了呗,但是这样判断就很麻烦,比较耗时间,如果我们每一次能失去这个位置能否放置皇后的判断,时间复杂度将会降低不少吧?可这也意味着我们必须达到每一次搜索都能精准的判断出下一次放置的位置在哪里,这便有了五个要素的判断。
1)这个位置本身题目要求就不能放,这就没办法了,只能用二维数组来存了如果是‘ . ’,那么就存为1,表示不能放,否则为0。1和0你们会想到什么,这就是二进制,那么我们是否可以改存成一维数组呢?举个栗子:
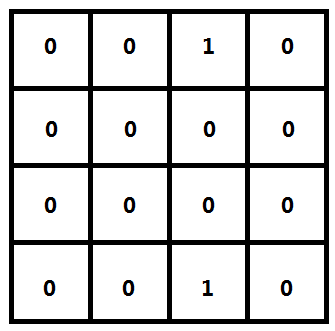
这样我们是不是就可以以十进制存储二进制的方式存下每一行,定义一个数组map,按此图为例,那么map[1]=4,也就是(0010)₂,这里默认大家二进制会一些基础知识。
【前方高能】
2)在行上的冲突:这就很容易了,每放完一个皇后之后,只要把当前行号+1就可以了,比如现在在第二行放了一个皇后,那么下一次放就会在第三行(也就是2+1=3(行))。
3)在列上的冲突:众所周知,皇后更攻击的范围包括了它所在的这一列,这样进行操作很简单,比如在第三列放了一个皇后,那么这一列永远也不能放置皇后了。
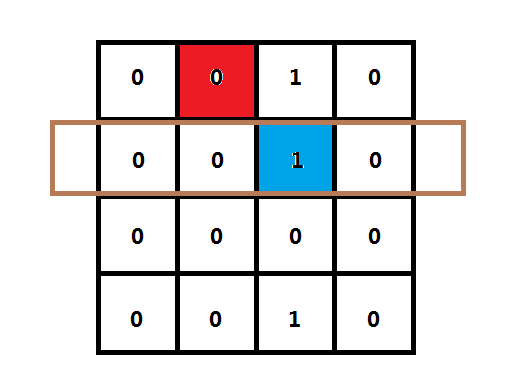
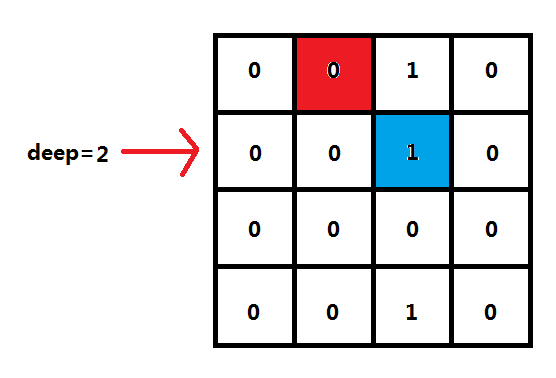
那么说了,这么多,用什么来表示行列上的状态呢?行上就不必多说了,直接递归时行数的参数加1就可以了。那么列呢?也要用二进制,举个栗子:

按照上面的图来说:这次我要在红色格子上放一次皇后,那么我下一次放置,哪些地方已经不能放了呢?显然,如下图所示的蓝色格子和第一行(因此表示行号的参数加1)已经不能放了。
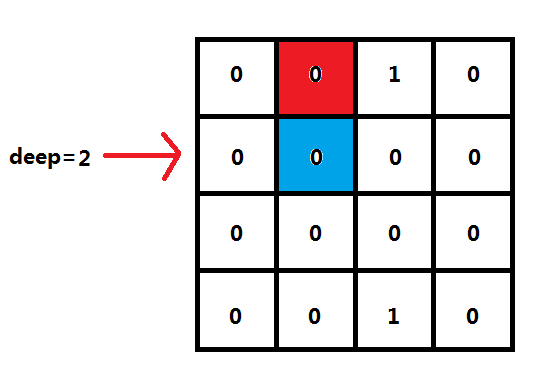
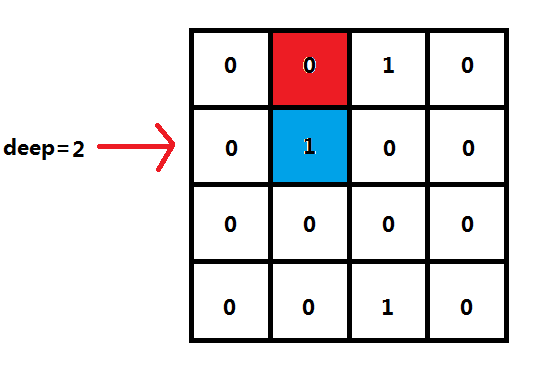
那么蓝色格子就会标记为1。下一行的列将会从(0000)₂更改成(0100)₂。
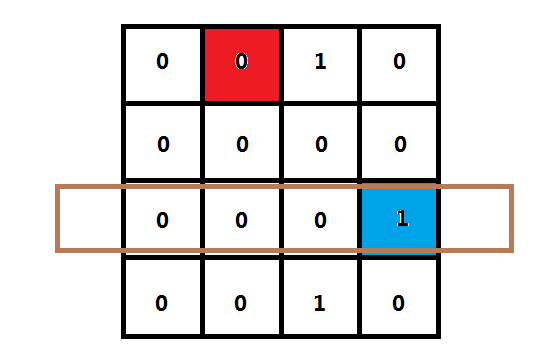
4)左上到右下的对角线:我们依旧使用二进制来存储,如下图(还是同样的位置、同样的图):

小编依旧要在红色格子上放置皇后,那么下一行哪些格子会因为左上到右下的对角线而不能放呢?如图所示,蓝色格子就一定不能。
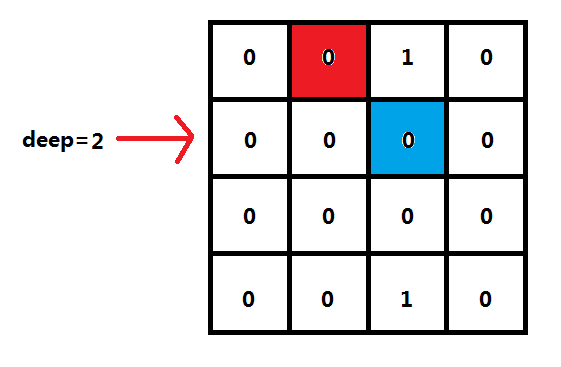
然后标记为1,于是表示左上到右下的对角线二进制值从(0000)₂变到了(0010)₂。
4)右上到左下的对角线:同上,只不过会影响到下一行的左边而不是右边,从(0000)₂变到了(1000)₂ 。
我想这些都应该很好理解吧,这是很简单易懂的,以这个栗子为栗,整理(0010)₂、(1000)₂、(0100)₂,用异或(符号:|)的方法合并成(1110)₂,这时我们能轻易的发现下一行的第四位一定是可以放皇后的,因为第四位是0,可是电脑不断找0是浪费时间的,但是找1是却是简单了,现将(1110)₂取反变成(0001)₂,那么又怎么找1?还记得树状数组中有个lowbit(假设有一个数x,那么x&-x便是lowbit(x)的值)吗?利用lowbit原理(恕小编不才,不会证明,但只要记住这个函数可以取到一个数的二进制数的最右边的1),就可以找到1的位置(也就是取反前0的位置),然后递归这个位置即可,因为可能下一行有>1个位置可以放皇后,所以要减去这个1,再找下一个1,然后继续进行递归。
【前方高能】
问题又来了!这个搜索该怎么写?我想你现在一定满肚子问题,现在小编就来回答一下这些问题,看一看与你现在想的一样不一样!
Q:递归参数怎么写?有哪些要素组成?
A:递归参数还是比较简单的,只需要4个参数,分别是行、列。左上到右下的对角线和右上到左下的对角线的状态。
Q:这些状态怎么表示?
A:全部使用二进制,1表示当前位置不可放,0表示当前位置可以放。
Q:这些二进制表示的状态是怎么存储的,一直在说是二进制,到底怎么判断?
A:一直在说二进制是为了好理解,但是我们要存成十进制的数,如(1011)₂要存成的数值为13。
Q:为什么看到亮出的代码上会有mod=(1<<n)-1;和int pos=mod&(~(line|lr|rl|map[deep])),p;呢?mod到底是用来干啥的?
A:注意:我们的二进制表示数一定只有n位,比如是4*4的棋盘,那么一定二进制表示出的数只有4位,举个栗子:当在第一行第一位放置一个皇后之后,那么下一行右上到左下的二进制表示的数为(10000)₂,那么将会多出去一位,为了保持计算的范围不变,那么如果我们用(10000)₂ &(1111)₂,那么结果将会取两个数都是1的位,由于这两个数没有二进制下相同的1的位,所以全部取0,所以下一行右上到左下的二进制表示的数会变成(0000)₂。其中mod就是(1111)₂,以n=4为例,自己计算一下便会知道mod=(1111)₂。
Q:pos&-pos是什么鬼?
A:注意看上面的解释,这句话可以当做lowbit(pos),实在不理解就只能去恶补树状数组了。
Q:实在不理解dfs(deep+1,line+p,(lr+p)<<1,(rl+p)>>1);,肿么办?
A:那我详细解释一下:deep是行号的意思,下一次放置皇后当然会在下一行喽;那么line呢?这个参数是用来表示列的状态的,比如说原来列的状态是(1001)₂(表示1,4列已有皇后放置),现在要在p(0100)₂(表示在下一行第二个位置放置皇后) 的位置摆放一个皇后,那么下一次列的状态将会是当前的状态(1001)₂+下一次要放皇后的位置(0100)₂=(1101)₂(从表示1,4列已有皇后放置变成了表示1,2,4列已有皇后放置)喽;斜着的对角线便是一大难点,为什么要左移(右移)?这是因为对角线是斜着的,举个栗子:比如说小编现在这一行表示左上到右下的对角线的二进制表示数为(0010)₂,那么这个红色方块内的棋子会通过左上到右下的对角线影响到第三行哪些格子呢?很显然是第三个位置上的棋子,此时第三行的状态将从(0000)₂改为(0001)₂,这有什么规律呢?当然是第三位的1变成了下一行第四位的1,向右移了1位,因此下一行要向右(向左)移。实在不理解文字描述,可以看下面的flash动画。