前面我们提到输入的数据正好是升序或降序序列时,二叉排序树就会退化成一个单链表,时间复杂度变为 O(N)(如果没看前面,点这里),这是我们所不希望的。我们也提出了解决办法,那就是“平衡”BST树。
AVL树:最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为1,所以它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下的时间复杂度都是O(log{n}),增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。AVL树得名于它的发明者G. M. Adelson-Velsky和E. M. Landis,他们在1962年的论文《An algorithm for the organization of information》中发表了它。
具体代码实现与分析:
1.节点定义
class Node
{
public:
int key = 0;
int height = 0;
Node *left = nullptr;
Node *right = nullptr;
Node(int key_t = 0)
{
key = key_t;
height = 1;
left = right = nullptr;
}
};2. 四种平衡操作
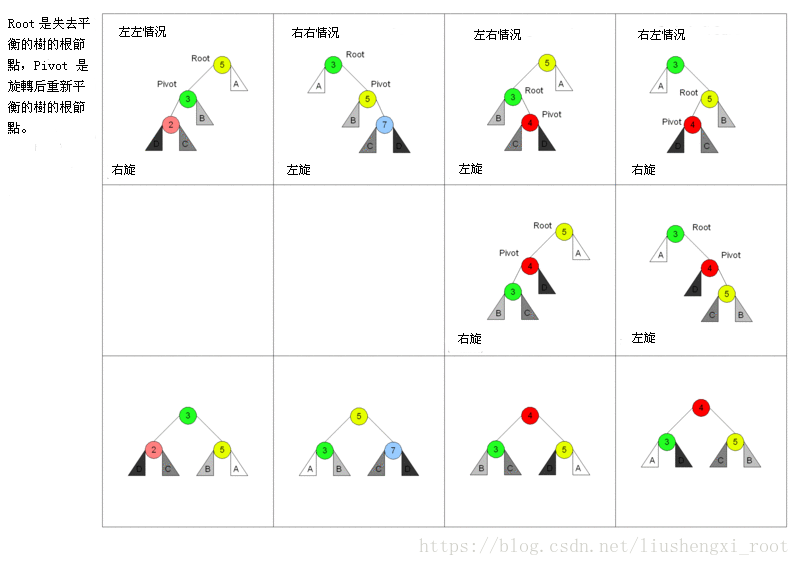
在我们进行完插入或删除操作后,很可能会导致某个结点失去平衡,那么我们就需要把失衡结点旋转一下,使其重新恢复平衡。经过总结,所谓的失衡,不管怎样,只有以下四种情况。
(以下统一约定:红色结点为新插入结点,y 结点为失衡结点)
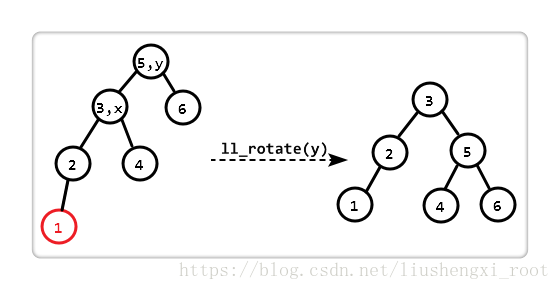
左左失衡
所谓的左左,即 “失衡结点” 的左子树比右子树高 2,左孩子(即 x)下的左子树比右子树高 1。
我们只需对 “以 y 为根的子树” 进行 “左左旋转 (ll_rotate)” 即可。一次旋转后,恢复平衡。
Node *AVL::ll_ratate(Node *y)
{
Node *x = y->left;
y->left = x->right;
x->right = y;
y->height = max(get_height(y->left), get_height(y->right)) + 1;
x->height = max(get_height(x->left), get_height(x->right)) + 1;
return x; //返回根节点
}右右失衡:
所谓的右右,即 “失衡结点” 的右子树比左子树高 2,右孩子(即 x)下的右子树比左子树高 1。
我们只需对 “以 y 为根的子树” 进行 “右右旋转 (rr_rotate)” 即可。一次旋转后,恢复平衡。
Node *AVL::rr_ratate(Node *y)
{
Node *x = y->right;
y->right = x->left;
x->left = y;
y->height = max(get_height(y->left), get_height(y->right)) + 1;
x->height = max(get_height(x->left), get_height(x->right)) + 1;
return x;
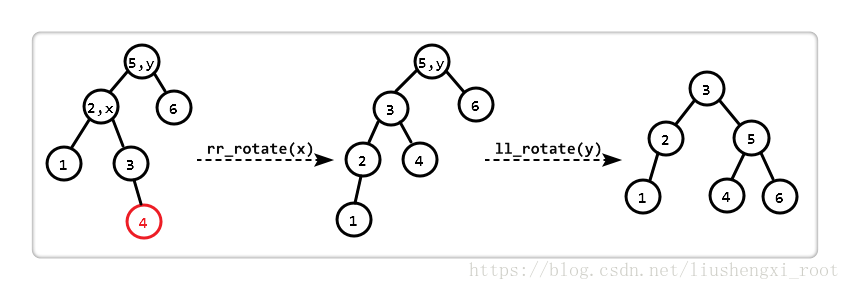
}左右失衡
所谓的左右,即 “失衡结点” 的左子树比右子树高 2,左孩子(即 x)下的右子树比左子树高 1。
观察发现,若先对 “以 x 为根的子树” 进行 “右右旋转 (rr_rotate)”,此时 “以 y 为根的子树” 恰好符合 “左左失衡”,所以再进行一次 “左左旋转 (ll_rotate)”。两次旋转后,恢复平衡。
Node *AVL::lr_ratate(Node *y)
{
Node *x = y->left;
y->left = rr_ratate(x);
return ll_ratate(y);
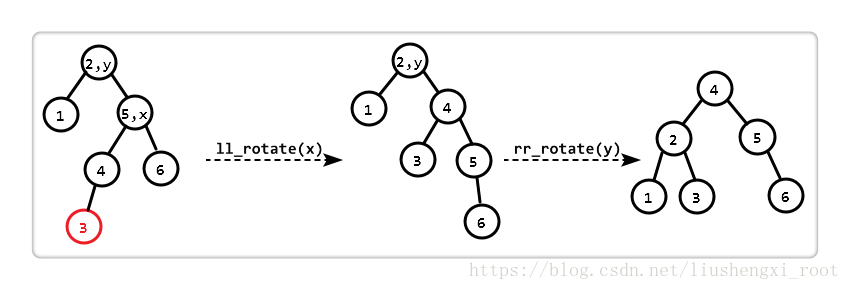
}右左失衡
所谓的右左,即 “失衡结点” 的右子树比左子树高 2,右孩子(即 x)下的左子树比右子树高 1。
观察发现,若先对 “以 x 为根的子树” 进行 “左左旋转 (ll_rotate)”,此时 “以 y 为根的子树” 恰好符合 “右右失衡”,所以再进行一次 “右右旋转 (rr_rotate)”。两次旋转后,恢复平衡。
Node *AVL::rl_ratate(Node *y)
{
Node *x = y->right;
y->right = ll_ratate(x);
return rr_ratate(y);
}3. 插入操作
插入成功后,在递归回溯时依次对经过的结点判断是否失衡,若失衡就需要对其进行对应的旋转操作使其恢复平衡,在这期间,原先作为一棵子树的根结点就会因为旋转被替换,因此设置insert_real()返回的是新根结点,这样就可以实时更新根结点。
void AVL::insert(int key)
{
header->left = insert_real(key, header->left);
}
Node *AVL::insert_real(int key, Node *node) //返回新的根节点,用来更新根节点
{
if (node == nullptr)
return new Node(key);
if (key < node->key)
node->left = insert_real(key, node->left);
else if (key > node->key)
node->right = insert_real(key, node->right);
else
return node;
node->height = max(get_height(node->left), get_height(node->right)) + 1;
//因为新加入了一个节点,所以回溯的时候给各个节点高度 +1
int balance = get_balance(node); //左减右
// 左左失衡
/*即 "失衡结点" 的左子树比右子树高 2,左孩子(即 x)下的左子树比右子树高 1*/
if (balance > 1 && get_balance(node->left) > 0)
return ll_ratate(node);
//右右失衡
/*"失衡结点" 的右子树比左子树高 2,右孩子(即 x)下的右子树比左子树高 1。*/
if (balance < -1 && get_balance(node->right) < 0)
return rr_ratate(node);
// 左右失衡
/*"失衡结点" 的左子树比右子树高 2,左孩子(即 x)下的右子树比左子树高 1。。*/
if (balance > 1 && get_balance(node->left) < 0)
return lr_ratate(node);
// 右左失衡
/*""失衡结点" 的右子树比左子树高 2,右孩子(即 x)下的左子树比右子树高 1。*/
if (balance < -1 && get_balance(node->right) > 0)
return rl_ratate(node);
return node;
}4. 删除操作
void AVL::erase(int key)
{
header->left = erase_real(key, header->left);
}
Node *AVL::erase_real(int key, Node *node)
{
if (node == nullptr)
{
cout << key << "不在该 AVL 树中" << endl;
return node;
}
if (key < node->key)
node->left = erase_real(key, node->left);
else if (key > node->key)
node->right = erase_real(key, node->right);
else
{
if (node->left && node->right)
{
// 找到后继结点
Node *x = node->right;
while (x->left)
x = x->left;
// 后继直接复制
node->key = x->key;
// 转化为删除后继
node->right = erase_real(x->key, node->right);
}
else
{
Node *t = node;
node = node->left ? node->left : node->right;
delete t;
if (node == nullptr)
return nullptr;
}
}
node->height = max(get_height(node->left), get_height(node->right)) + 1;
int balance = get_balance(node);
// 左左失衡
if (balance > 1 && get_balance(node->left) >= 0) // 需要加等号
return ll_ratate(node);
// 右右失衡
if (balance < -1 && get_balance(node->right) <= 0) // 需要加等号
return rr_ratate(node);
// 左右失衡
if (balance > 1 && get_balance(node->left) < 0)
return lr_ratate(node);
// 右左失衡
if (balance < -1 && get_balance(node->right) > 0)
return rl_ratate(node);
return node;
}为什么需要加等号?因为会出现 get_balance(node->left) == 0 的情况啊,自然必须得去由左左和右右函数去处理。
5.查找操作比较简单,同BST树即可。
6.完整代码:
/*************************************************************************
> File Name: myhead.h
> Author: Liu Shengxi
> Mail: 13689209566@163.com
> Created Time: 2018年07月26日 星期四 22时59分58秒
************************************************************************/
#ifndef _MYHEAD_H
#define _MYHEAD_H
#include<vector>
class Node
{
public:
int key = 0;
int height = 0;
Node *left = nullptr;
Node *right = nullptr;
Node(int key_t = 0)
{
key = key_t;
height = 1;
left = right = nullptr;
}
};
class AVL
{
private:
Node *header; //header结点并非根结点,header->left指向的才是根结点。
Node *ll_ratate(Node *y);
Node *rr_ratate(Node *y);
Node *lr_ratate(Node *y);
Node *rl_ratate(Node *y);
int get_height(Node *node);
int get_balance(Node *node);
Node *insert_real(int key, Node *node);
Node *&find_real(int key, Node *&node);
Node *erase_real(int key, Node *node);
void in_order(Node *root); //中序遍历
void root_order(Node *root); // 先序遍历
void after_order(Node *root); //后序遍历
int destory(Node *node);
public:
AVL();
~AVL();
void insert(int key);
// (递归实现)查找"AVL"中键值为key的节点
Node *find(int key);
//(非递归实现)查找"AVL"中键值为key的节点
Node *loop_find(int key);
void erase(int key);
void print(int tag);
};
#endif
#include <iostream>
#include <sstream>
#include <string>
#include "myhead.h"
#include <algorithm>
using namespace std;
AVL::AVL()
{
header = new Node(-100);
}
AVL::~AVL()
{
destory(header->left); //将多余的那个节点也删除掉
}
int AVL::destory(Node *p)
{
if (p == nullptr)
return 0;
// test++;
// cout << "test == " << test << endl;
destory(p->left); //注意先后次序,如果先把p销毁,那么就会找不到p->left,p->right
destory(p->right);
delete p;
p = nullptr;
}
void AVL::insert(int key)
{
header->left = insert_real(key, header->left);
}
int AVL::get_height(Node *node)
{
if (node == nullptr)
return 0;
return node->height;
}
int AVL::get_balance(Node *node)
{
if (node == nullptr)
return 0;
return get_height(node->left) - get_height(node->right);
}
Node *AVL::insert_real(int key, Node *node) //返回新的根节点,用来更新根节点
{
if (node == nullptr)
return new Node(key);
if (key < node->key)
node->left = insert_real(key, node->left);
else if (key > node->key)
node->right = insert_real(key, node->right);
else
return node;
node->height = max(get_height(node->left), get_height(node->right)) + 1;
//因为新加入了一个节点,所以回溯的时候给各个节点高度 +1
int balance = get_balance(node); //左减右
// 左左失衡
/*即 "失衡结点" 的左子树比右子树高 2,左孩子(即 x)下的左子树比右子树高 1*/
if (balance > 1 && get_balance(node->left) > 0)
return ll_ratate(node);
//右右失衡
/*"失衡结点" 的右子树比左子树高 2,右孩子(即 x)下的右子树比左子树高 1。*/
if (balance < -1 && get_balance(node->right) < 0)
return rr_ratate(node);
// 左右失衡
/*"失衡结点" 的左子树比右子树高 2,左孩子(即 x)下的右子树比左子树高 1。。*/
if (balance > 1 && get_balance(node->left) < 0)
return lr_ratate(node);
// 右左失衡
/*""失衡结点" 的右子树比左子树高 2,右孩子(即 x)下的左子树比右子树高 1。*/
if (balance < -1 && get_balance(node->right) > 0)
return rl_ratate(node);
return node;
}
void AVL::print(int tag)
{
if (tag == 1)
{
cout << " 先序遍历 : " << endl;
root_order(header->left);
cout << endl;
}
if (tag == 2)
{
cout << " 中序遍历 : " << endl;
in_order(header->left);
cout << endl;
}
if (tag == 3)
{
cout << " 后序遍历 : " << endl;
after_order(header->left);
cout << endl;
}
}
void AVL::after_order(Node *root)
{
if (root != nullptr)
{
after_order(root->left);
after_order(root->right);
cout << "[ " << root->key << " ," << root->height << " ]" << endl;
}
}
void AVL::in_order(Node *root)
{
if (root != nullptr)
{
in_order(root->left); //先打印右子树
cout << "[ " << root->key << " ," << root->height << " ]" << endl;
in_order(root->right);
}
}
void AVL::root_order(Node *root)
{
if (root != nullptr)
{
cout << "[ " << root->key << " ," << root->height << " ]" << endl;
root_order(root->left); //先打印右子树
root_order(root->right);
}
}
Node *AVL::ll_ratate(Node *y)
{
Node *x = y->left;
y->left = x->right;
x->right = y;
y->height = max(get_height(y->left), get_height(y->right)) + 1;
x->height = max(get_height(x->left), get_height(x->right)) + 1;
return x; //返回根节点
}
Node *AVL::rr_ratate(Node *y)
{
Node *x = y->right;
y->right = x->left;
x->left = y;
y->height = max(get_height(y->left), get_height(y->right)) + 1;
x->height = max(get_height(x->left), get_height(x->right)) + 1;
return x;
}
Node *AVL::lr_ratate(Node *y)
{
Node *x = y->left;
y->left = rr_ratate(x);
return ll_ratate(y);
}
Node *AVL::rl_ratate(Node *y)
{
Node *x = y->right;
y->right = ll_ratate(x);
return rr_ratate(y);
}
Node *AVL::find(int key)
{
return find_real(key, header->left);
}
Node *&AVL::find_real(int key, Node *&node)
{
if (node == nullptr)
return node;
if (key < node->key)
find_real(key, node->left);
else if (key > node->key)
find_real(key, node->right);
else // 只剩下相等了
return node;
}
Node *AVL::loop_find(int key)
{
Node *p = header->left; // p 指向根节点
while (p && p->key != key)
{
if (key < p->key)
p = p->left;
else
p = p->right;
}
return p;
}
Node *AVL::erase_real(int key, Node *node)
{
if (node == nullptr)
{
cout << key << "不在该 AVL 树中" << endl;
return node;
}
if (key < node->key)
node->left = erase_real(key, node->left);
else if (key > node->key)
node->right = erase_real(key, node->right);
else
{
if (node->left && node->right)
{
// 找到后继结点
Node *x = node->right;
while (x->left)
x = x->left;
// 后继直接复制
node->key = x->key;
// 转化为删除后继
node->right = erase_real(x->key, node->right);
}
else
{
Node *t = node;
node = node->left ? node->left : node->right;
delete t;
if (node == nullptr)
return nullptr;
}
}
node->height = max(get_height(node->left), get_height(node->right)) + 1;
int balance = get_balance(node);
// 左左失衡
if (balance > 1 && get_balance(node->left) >= 0) // 需要加等号
return ll_ratate(node);
// 右右失衡
if (balance < -1 && get_balance(node->right) <= 0) // 需要加等号
return rr_ratate(node);
// 左右失衡
if (balance > 1 && get_balance(node->left) < 0)
return lr_ratate(node);
// 右左失衡
if (balance < -1 && get_balance(node->right) > 0)
return rl_ratate(node);
return node;
}
void AVL::erase(int key)
{
header->left = erase_real(key, header->left);
}
int main(void)
{
AVL avl;
// test "insert"
vector<int> intVec{3, 2, 1, 4, 4, 5, 6, 7, 10, 9, 7, 8};
for (auto i : intVec)
avl.insert(i);
avl.print(1);
//test "find"
Node *p = nullptr;
cout << ((p = avl.find(2)) ? p->key : -1) << endl; // 2
cout << ((p = avl.find(100)) ? p->key : -1) << endl; // -1
cout << ((p = avl.loop_find(14)) ? p->key : -1) << endl; // 测试找不到 -1
cout << ((p = avl.loop_find(5)) ? p->key : -1) << endl; // 测试找到 5
// test "erase"
avl.erase(100);
avl.print(2);
avl.erase(9);
avl.print(3);
avl.erase(8);
avl.print(3);
return 0;
}运行结果:
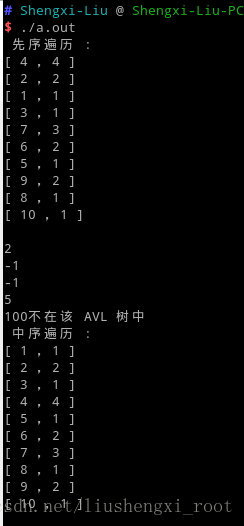
不知道大家有没有发现,我们的 BF 是从叶子节点向上递增的。(这个只是我们所这样规定的,可以自己改变)
参考链接:https://subetter.com/articles/2018/06/avl-tree.html
最后,为了让读者提提神,列出作为一名合格的程序员还需要学习的其他的树: