【DP】解析悬线法

例题传送门：https://www.luogu.com.cn/problem/P4147
大意：给出一张格子图，部分格子有障碍物，对于格子图上的所有矩形，我们称不包含障碍物的矩形为合法的，求合法的矩形的最大面积。

核心

对于每个点 ((i,j)) ，求出其向上扩张最大距离后所能围成都最大矩形面积，则答案为 所有点向上扩张最大距离后所能围成的最大矩形面积所构成的集合中的最大值。

点 ((i,j)) 指第 (i) 行，第 (j) 列的点。

如何理解上面那句话？
如图：黑格子为障碍物，蓝色格子为当前点。

向上扩张后（红色格子为扩张区域），我们得到：

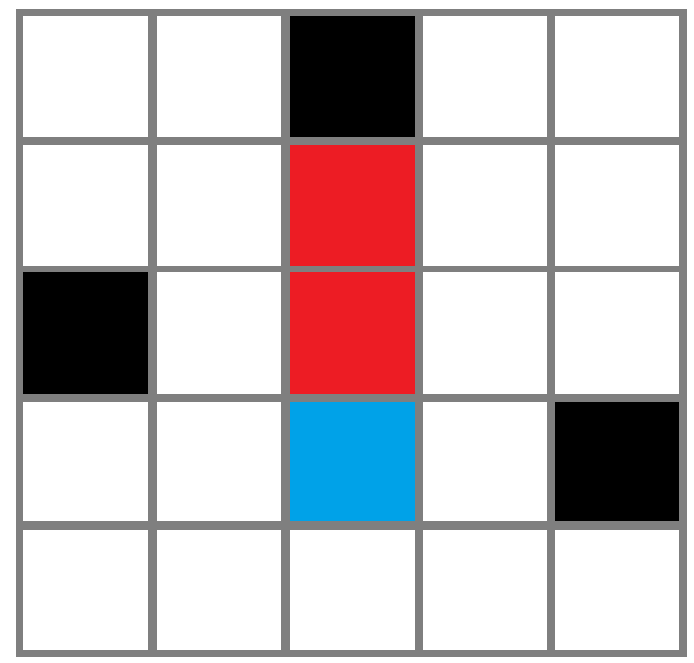
红色和蓝色部分是不是很像从上面（图的上边界或当前点向上数的第一个障碍点）垂下来的线？悬线法因此得名。

然后这条“线”向左右最大地扩张得到的面积就是蓝色格子（当前点）的向上扩张最大距离后所能围成都最大矩形面积。

如图：（所有绿色格子对应所求的面积）

证明：所有点向上扩张最大距离后所能围成都最大矩形面积所构成的集合包含合法的矩形的最大面积
假设合法的矩形的最大面积对应的矩形不在上述集合里，那么对应的矩形一定还可以向上扩张，得到的面积更大，矛盾。

具体步骤

定义:
(l[i][j]) 为点 ((i,j)) 向上扩张后所对应的线能够所能到达的最左边的位置。
(r[i][j]) 为点 ((i,j)) 向上扩张后所对应的线能够所能到达的最右边的位置。
(u[i][j]) 为点 ((i,j)) 可以向上扩张的最大距离（包括自己）。

预处理：
求出每个点能够向左、向右（这里不是向上扩张的线，而是当前点）走到的最远点对应的位置,以及向上走的最远距离。

void init(){
	// init l[][]
	for(int i=1;i<=n;i++)
		for(int j=2;j<=m;j++)
			if(g[i][j-1]) l[i][j]=l[i][j-1];
	
	// init r[][]
	for(int i=1;i<=n;i++)
		for(int j=m-1;j;j--)
			if(g[i][j+1]) r[i][j]=r[i][j+1];
	
	// init u[][]
	for(int i=2;i<=n;i++)
		for(int j=1;j<=m;j++)
			if(g[i-1][j]) u[i][j]=u[i-1][j]+1;
}

在转移的时候，求一下：

l[i][j]=max(l[i][j],l[i-1][j]), r[i][j]=min(r[i][j],r[i-1][j]);

该点产生的贡献（向上扩张最大距离后所能围成都最大矩形面积）就是：

u[i][j]*(r[i][j]-l[i][j]+1)

其他细节请结合代码理解：

#include<bits/stdc++.h>
using namespace std;

const int N=1005;
int n,m;
bool g[N][N];
int l[N][N],r[N][N],u[N][N]; 

void init(){
	// init l[][]
	for(int i=1;i<=n;i++)
		for(int j=2;j<=m;j++)
			if(g[i][j-1]) l[i][j]=l[i][j-1];
	
	// init r[][]
	for(int i=1;i<=n;i++)
		for(int j=m-1;j;j--)
			if(g[i][j+1]) r[i][j]=r[i][j+1];
	
	// init u[][]
	for(int i=2;i<=n;i++)
		for(int j=1;j<=m;j++)
			if(g[i-1][j]) u[i][j]=u[i-1][j]+1;
}

int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++){
			char ch; cin>>ch;
			g[i][j]= ch=='F'?1:0;
			l[i][j]=r[i][j]=j;
			u[i][j]=1;
		}
		
	init(); // 预处理出每个点能够向左、向右、走到的最远点对应的位置,以及向上走的最远距离。
	
	int res=0;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			if(!g[i][j]) continue;
			if(i>1 && g[i-1][j]){
				l[i][j]=max(l[i][j],l[i-1][j]), r[i][j]=min(r[i][j],r[i-1][j]);
			}
			res=max(res,u[i][j]*(r[i][j]-l[i][j]+1));	
		}
	}
		
	cout<<res*3<<endl;
	
	return 0;
}