长链剖分学习笔记

什么事长链剖分：

• 对于每个节点令其子树高度最大的儿子的边为实边，其余边为虚边。
• 于是树可以剖成由实边组成的若干长链。
• 同重剖类似，有一个结论：对于任意节点 (u)，其到根的路径的上的虚边数量（长链数量）是 (O(sqrt n)) 级别。

CF1009F Dominant Indices

对于每个节点 (u)，求出一个最小的 (k)，使得 (u) 子树中到 (u) 距离为 (k) 的点的数量最大。

对于每个点 (f(u,d)) 表示 (u) 子树内到 (u) 的距离为 (d) 的节点个数。如果直接存储会炸裂。我们发现其实求 (u) 的信息完全可以直接利用一些在子节点求得的信息然后再往上增量。这点信息，不需要 copy，直接用指针即可。

我们考虑对于每一个长链申请一个空间。从指针理解，(f_u) 表示 (f_u(d)) 数组的头指针。对于节点 (u)，设它的实边儿子为 (v)，则让 (f_v=f_u+1)，即长成这样：

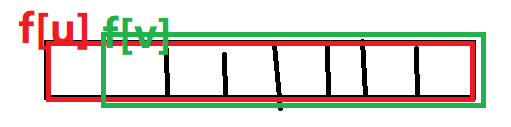
然后对于每个节点，我们不仅从 (v) 上直接得到信息，还需要合并所有虚边连向的长链。这个普通转移即可。

对于复杂度，每条长链最多被合并一次，而合并一次的复杂度为其链长，所以总复杂度为 (sum len=O(n))。而空间复杂度也一样，每条链所需空间为链长，同样得到 (O(n))。

对于分配内存，维护一个指针，指向一个数组的位置，然后将长 (dep+1) 的一段分配给它。

内存分配还是开大一点好。

https://codeforces.com/contest/1009/submission/133302570

const int N=1e6+9;
int n,h[N],son[N],g[N<<1],*f[N],ans[N],*cur=g;
vi e[N];

void dfs1(int u,int fa) {
	for(auto v:e[u]) if(v!=fa) {
		dfs1(v,u);
		if(h[v]>=h[son[u]]) son[u]=v, h[u]=h[v]+1;
	}
}
void dfs2(int u,int fa) {
	if(son[u]) {
		f[son[u]]=f[u]+1, dfs2(son[u],u), ans[u]=ans[son[u]]+1;
	}
	int mh=0;
	for(auto v:e[u]) if(v!=fa&&v!=son[u]) {
		f[v]=cur, cur+=h[v]+1;
		dfs2(v,u);
		rep(i,0,h[v]) f[u][i+1]+=f[v][i];
		mh=max(mh,h[v]+1);
	}
	f[u][0]=1;
	rep(i,0,mh)
		if(f[u][i]>f[u][ans[u]]||f[u][i]==f[u][ans[u]]&&i<ans[u]) ans[u]=i;
}

int main() {
	n=read();
	rep(i,2,n) {
		int u=read(), v=read();
		e[u].emplace_back(v), e[v].emplace_back(u);
	}
	dfs1(1,0);
	f[1]=cur, cur+=h[1]+1; dfs2(1,0);
	rep(i,1,n) printf("%d
",ans[i]);
	return 0;
}

经典题

求树上长度（路径点数）恰好为 (k) 的路径数量。

考虑在合并链的时候统计一下跨过 (u) 的链的数量即可。

const int N=3e5+9;
int n,k,ans,son[N],h[N],g[N<<1],*f[N],*cur=g;
vi e[N];

void dfs1(int u,int fa) {
	for(auto v:e[u]) if(v!=fa) {
		dfs1(v,u);
		if(h[v]>=h[son[u]]) son[u]=v;
	} h[u]=h[son[u]]+1;
}
void dfs2(int u,int fa) {
	if(son[u]) {
		f[son[u]]=f[u]+1, dfs2(son[u],u); if(h[u]>=k) ans+=f[u][k];
	} f[u][0]++;
	for(auto v:e[u]) if(v!=fa&&v!=son[u]) {
		f[v]=cur, cur+=h[v]+1;
		dfs2(v,u);
		rep(i,0,min(k,h[v])) if(k-i-1<=h[u]) ans+=f[u][k-i-1]*f[v][i];
		rep(i,0,h[v]) f[u][i+1]+=f[v][i];
	}
}
z
signed main() {
	n=read(), k=read();
	rep(i,2,n) {
		int u=read(), v=read();
		e[u].emplace_back(v), e[v].emplace_back(u);
	}
	dfs1(1,0), f[1]=cur, cur+=h[1]+1, dfs2(1,0);
	printf("%lld
",ans);
	return 0;
}

POI2014 Hotels

求树上选三点两两距离相等的方案数。

设 (f(u,i)) 表示子树中距离 (u) 为 (i) 的节点个数。然后考虑一种特殊情况，即三个点 (x,y,z) （相互距离为 (d) 且总体 (lca=u)）满足 (lca(y,z)) 到 (u) 的距离加上 (z) 到 (u) 的距离等于 (d)（即 (lca(y,z)) 到 (z) 的链跨过 (u)）。针对这种情况，我们设计状态 (g(u,i)) 表示存在多少这样的 (y,z) 满足到 (lca(y,z)) 距离相等（设之为 (d)），且 (lca(y,z)) 到 (u) 的距离为 (d-i)。

所以答案为（若 (u,v) 同时出现，此时意味着 (f(u)) 只是一个前缀，在和 (v) 合并时统计答案）

[ans=g(u,0) +sum_i sum_{vin son_u} f(u,i-1) imes g(v,i)+f(u,i-1) imes g(v,i)\ g(u,i)=sum g(v,i+1)+f(u,i) imes f(v,i-1) ]

长剖增量 DP 即可。

const int N=4e5+9,mod=1e9+7;
int n,*f[N],*g[N],h[N],p[N],*cur=p,son[N],ans;
vi e[N];

void dfs1(int u,int fa) {
	for(auto v:e[u]) if(v!=fa) {
		dfs1(v,u);
		if(h[v]>=h[son[u]]) son[u]=v;
	}
	h[u]=h[son[u]]+1;
}
void dfs2(int u,int fa) {
	if(son[u]) {
		f[son[u]]=f[u]+1, g[son[u]]=g[u]-1;
		dfs2(son[u],u); 
	} f[u][0]=1; ans+=g[u][0];
	for(auto v:e[u]) if(v!=fa&&v!=son[u]) {
		f[v]=cur, cur+=h[v]*2, g[v]=cur, cur+=h[v]*2;
		dfs2(v,u);
		rep(i,0,h[v]-1) ans+=g[u][i+1]*f[v][i], ans%=mod;
		rep(i,1,h[v]-1) ans+=f[u][i-1]*g[v][i], ans%=mod;
		rep(i,0,h[v]-1) g[u][i+1]+=f[u][i+1]*f[v][i];
		rep(i,1,h[v]-1) g[u][i-1]+=g[v][i]; 
		rep(i,0,h[v]-1) f[u][i+1]+=f[v][i];
	}
}

signed main() {
	n=read();
	rep(i,2,n) {
		int u=read(), v=read();
		e[u].emplace_back(v), e[v].emplace_back(u);
	}
	dfs1(1,0), f[1]=cur, cur+=h[1]*2, g[1]=cur, cur+=h[1]*2, dfs2(1,0);
	printf("%lld
",ans);
	return 0;
}