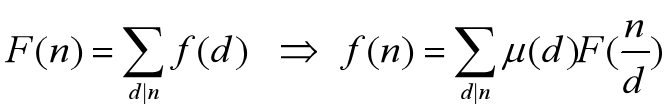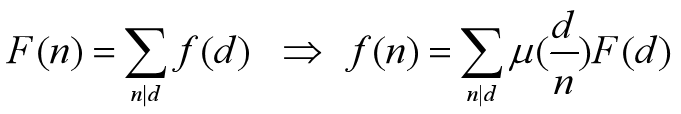先看大佬的PPT:点击打开链接
那么莫比乌斯反演主要解决什么问题呢?它主要解决的是对于一些函数f(n),如果我们很难直接求出它的值,而容易求出倍数和或约数和F(n),那么我们可以通过莫比乌斯反演来求得f(n)的值。
莫比乌斯反演实现代码:
mu[1]=1;
for(i=2;i<=n;i++)
{
if(!not_prime[i])
{
prime[++tot]=i;
mu[i]=-1;
}
for(j=1;prime[j]*i<=n;j++)
{
not_prime[prime[j]*i]=1;
if(i%prime[j]==0)
{
mu[prime[j]*i]=0;
break;
}
mu[prime[j]*i]=-mu[i];
}
}
主要用的是第二种形式。
接下来举一道例题:
2301: [HAOI2011]Problem b
Time Limit: 50 Sec Memory Limit: 256 MBSubmit: 6276 Solved: 2876
[Submit][Status][Discuss]
Description
对于给出的n个询问,每次求有多少个数对(x,y),满足a≤x≤b,c≤y≤d,且gcd(x,y) = k,gcd(x,y)函数为x和y的最大公约数。
Input
第一行一个整数n,接下来n行每行五个整数,分别表示a、b、c、d、k
Output
共n行,每行一个整数表示满足要求的数对(x,y)的个数
Sample Input
2
2 5 1 5 1
1 5 1 5 2
2 5 1 5 1
1 5 1 5 2
Sample Output
14
3
HINT
100%的数据满足:1≤n≤50000,1≤a≤b≤50000,1≤c≤d≤50000,1≤k≤50000
代码实现(by hzwer):
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<set>
#include<ctime>
#include<vector>
#include<cmath>
#include<algorithm>
#include<map>
#define ll long long
using namespace std;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int tot;
int a,b,c,d,k;
int sum[50005],mu[50005],pri[50005];
bool mark[50005];
void getmu()
{
mu[1]=1;
for(int i=2;i<=50000;i++)
{
if(!mark[i]){mu[i]=-1;pri[++tot]=i;}
for(int j=1;j<=tot&&i*pri[j]<=50000;j++)
{
mark[i*pri[j]]=1;
if(i%pri[j]==0){mu[i*pri[j]]=0;break;}
else mu[i*pri[j]]=-mu[i];
}
}
for(int i=1;i<=50000;i++)
sum[i]=sum[i-1]+mu[i];
}
int cal(int n,int m)
{
if(n>m)swap(n,m);
int ans=0,pos;
for(int i=1;i<=n;i=pos+1)
{
pos=min(n/(n/i),m/(m/i));
ans+=(sum[pos]-sum[i-1])*(n/i)*(m/i);
}
return ans;
}
int main()
{
getmu();
int T=read();
while(T--)
{
a=read();b=read();c=read();d=read();k=read();
a--;c--;
a/=k;b/=k;c/=k;d/=k;
int ans=cal(a,c)+cal(b,d)-cal(a,d)-cal(b,c);
printf("%d
",ans);
}
return 0;
}