SPOJ Linearian Colony （二分或规律）

题意：第0年有一个Linearians子（我也不知道这个是什么东西，反正是自交的...），是红色red。每一年所有的都会生新的Linearians子(同时他们生的颜色与他们本身颜色相反(我们定蓝色为红色的反色)。

所有Linearians排成一排，然后对应的孩子排在父辈前面.

例如：(我们把0看作红色，1看作蓝色)

第0年： 0

第1年：10

第2年：0110

第3年：10010110

.....

现在过了Y年（0<=Y<=51）排在第i个位置的Linearian为什么颜色.

正常思路：我们就是要判断查询位置是在前半部分还是后半部分，如果比mid小就往(l,mid)区间去继续递归找，否则折半，记录取反次数

#include <cstdio>
#include <algorithm>
#include <string>
#include <iostream>
#include <cstring>
#include <cmath>
#define ll long long
const int maxn=5e2+10;
using namespace std;
ll y,p;
int main(){
    ll sum =1;
    cin >>y>>p;
    p++;
    for(int i=1;i<=y;i++)
        sum*=2;
    int flag = 0; 
    ll l=1,r=sum;//左右端点
    while(l<r){
        ll mid = (l+r)/2;
        if(p<=mid){
            flag ++;
            r = mid;
        }
        else{
            l = mid+1;
        }
    } 
    //cout <<l<<r<< flag <<endl;
    if(flag%2)    cout <<"blue"<<endl;
    else    cout <<"red"<<endl; 
    return 0;
    
} 

二分（的确没错）但是我做题时发现比较有意思的地方（玄学规律）

如图：            

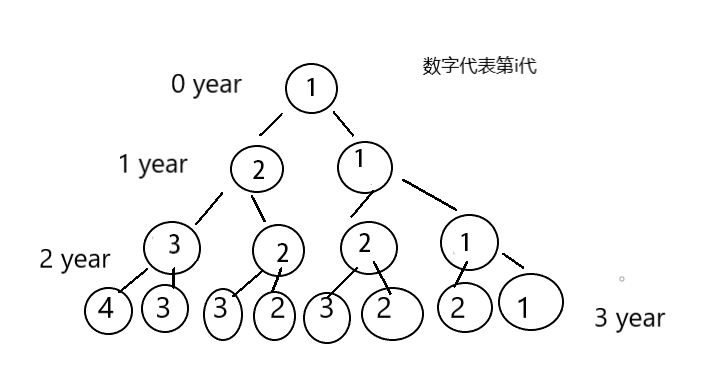
会发现 奇数部分 与上一层代数相同，偶数则是比上一层多一代

所以我们对我们通过最终得到的代数，可以知道颜色被转变了多少次，从而得到最后的颜色。同时由于子代是排在父代之前的，所以我们要先用长度减去询问的位置，来得到我们正向判断的位置

AC代码：

#include <cstdio>
#include <iostream>
#include <cstring>
#include <string>
#include <algorithm>
#include <cmath>
using namespace std;
long long n;
long long pos;
int flag;
int main(){
    while(cin>>n>>pos){
        int cont = 0;
        pos=(pow(2,n)-pos);
        while(pos!=1){
            if(pos&1){
                 pos=(pos+1)/2;
            }else{
                pos /=2;
                cont++;
            }
        }
        if(cont&1) cout<<"blue"<<endl;
        else cout<<"red"<<endl;
    }
}

。。。。所以规律这种东西，真的玄学啊