@description@
给定一个字符串 s,求有多少种方案可将其划分成偶数个段 (p_1, p_2, ..., p_k),使得 (p_i = p_{k-i+1})。
模 10^9 + 7。
2 ≤ |s| ≤ 10^6。
@solution@
回文划分有一个经典的做法。不过这道题并不完全是回文划分,需要进一步地转化。
构造串 t = (s_1s_ns_2s_{n-1}...),则对 t 的偶回文划分对应了原题的一个合法划分。
定义 dp[i] 表示前 i 个字符进行回文划分的方案数。因为要偶回文划分,所以假如 i 为奇数直接令 dp[i] = 0。
朴素的转移即构建回文自动机,求出以 i 为结束的所有回文串,然后把这些回文串进行转移。
考虑是否可以利用之前已经处理过的信息。如图:
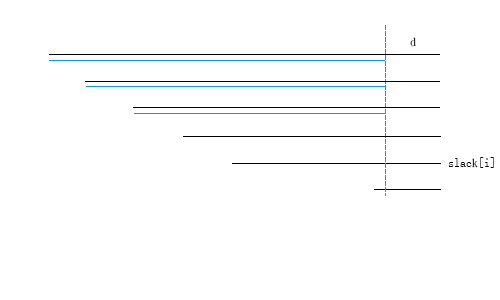
假如有若干回文串的长度形成以 d 为公差的等差数列(如图黑色线段),我们可以取 i-d 已经计算过的值(如图蓝色线段)方便我们转移。
具体一点,对于回文自动机上每一个结点 x,记 d(v) = len(v) - len(fa(v)),将 d(v) 相同的连续段称作一个等差数列(注意这里等差数列的定义)。
点 x 的最后更新位置 t 指的是,在前缀 t 所对应的最长回文后缀到根的路径中,x 是某一个等差数列中深度最大的点。
现在在回文树上的每个点维护:以他结尾的等差数列在其最后更新位置上的对应 dp 的和 f。
一个结论:若 d(v) = d(fa(v)),则 i - d(v) 是 fa(v) 的最后更新位置。
证明有两部分:首先证明没有 (i - d(v), i) 的位置更新 fa(v),然后再证明在 i - d(v) 这个地方 fa(v) 必定被更新。
因此直接取 fa(v) 维护好的 f 就是刚刚图中蓝色部分。
注意黑色部分还有一个回文串蓝色部分没有(slack[i] 上面那个串),需要单独拿出来处理。
另一个结论:一个回文串的所有回文串形成 O(log) 个等差数列。
回文后缀即回文串的 border,因此直接用 border 与周期的关系证明即可。
维护向上第一个 d(x) 与当前这个 d(v) 不相等的点,记 slack(v) = x。这样直接跳 slack 最多跳 log 次就到根了。
注意一点细节:当一个点的 fa = slack 时,它的 fa 不应该被算作贡献。
@accepted code@
#include <cstdio>
#include <cstring>
const int MAXN = 1000000;
const int MOD = int(1E9) + 7;
struct node{
int len, dif, f;
node *slk, *ch[26], *fa;
}pl[MAXN + 5], *rt1, *rt2, *ncnt;
node *nd[MAXN + 5];
void build(char *S, int len) {
rt1 = ncnt = pl, rt2 = (++ncnt);
rt2->fa = rt1, rt1->len = -1, rt2->len = 0;
node *pre = rt1;
for(int i=0;i<len;i++) {
while( S[i] != S[i - pre->len - 1] )
pre = pre->fa;
if( pre->ch[S[i] - 'a'] == NULL ) {
node *q = (++ncnt);
q->len = pre->len + 2;
if( pre == rt1 )
q->fa = rt2;
else {
node *p = pre->fa;
while( S[i] != S[i - p->len - 1 ] )
p = p->fa;
q->fa = p->ch[S[i] - 'a'];
}
q->dif = q->len - q->fa->len;
q->slk = (q->dif == q->fa->dif ? q->fa->slk : q->fa);
pre->ch[S[i] - 'a'] = q;
}
nd[i+1] = pre = pre->ch[S[i] - 'a'];
}
}
char s[MAXN + 5], t[MAXN + 5];
int dp[MAXN + 5];
int main() {
scanf("%s", s);
int len = strlen(s);
for(int i=0;i<len/2;i++)
t[(i<<1) + 1] = s[i], t[(i<<1|1) + 1] = s[len-i-1];
build(t + 1, len);
dp[0] = 1;
for(int i=1;i<=len;i++) {
node *p = nd[i];
while( p != rt2 ) {
p->f = dp[i - p->slk->len - p->dif];
if( p->slk != p->fa )
p->f = (p->f + p->fa->f) % MOD;
dp[i] = (dp[i] + p->f) % MOD;
p = p->slk;
}
if( i & 1 ) dp[i] = 0;
}
printf("%d
", dp[len]);
}
@details@
关键的代码不是很长。
一开始本来想写分奇偶回文串讨论着做,发现有点难搞。。。后来才发现可以直接把 dp 值强制改成 0。。。