CF786B Legacy && 线段树优化连边

线段树优化连边

要求点 (x) 向区间 ([L, R]) 连边， 一次的复杂度上限为 (O(n))
然后弄成线段树的结构

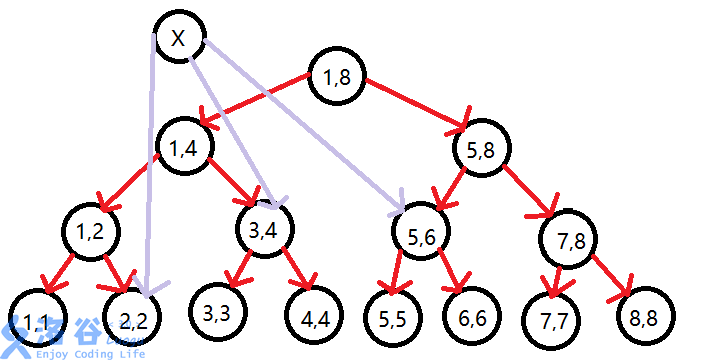
先父子连边边权为 (0)
这样连边就只需要连父亲就可以等效于连了区间内每个点
空间复杂度为线段树大小， 一次区间连边时间复杂度为 (O(log n))
这是连入边， 连出边的话反向建线段树内边即可

CF786B Legacy

默认情况下他不能用这把枪开启任何传送门。在网络上有q个售卖这些传送枪的使用方案。每一次你想要实施这个方案时你都可以购买它，但是每次购买后只能使用一次。每个方案的购买次数都是无限的。

网络上一共有三种方案可供购买： 1.开启一扇从星球v到星球u的传送门； 2.开启一扇从星球v到标号在[l,r]区间范围内任何一个星球的传送门。(即这扇传送门可以从一个星球出发通往多个星球) 3.开启一扇从标号在[l,r]区间范围内任何一个星球到星球v的传送门。(即这扇传送门可以从多个星球出发到达同一个星球)

Rick并不知道Morty在哪儿，但是Unity将要通知他Morty的具体位置，并且他想要赶快找到通往所有星球的道路各一条并立刻出发。因此对于每一个星球(包括地球本身)他想要知道从地球到那个星球所需的最小钱数。

Solution

线段树优化连边即可

Code

#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
#include<algorithm>
#define LL long long
#define REP(i, x, y) for(LL i = (x);i <= (y);i++)
using namespace std;
LL RD(){
    LL out = 0,flag = 1;char c = getchar();
    while(c < '0' || c >'9'){if(c == '-')flag = -1;c = getchar();}
    while(c >= '0' && c <= '9'){out = out * 10 + c - '0';c = getchar();}
    return flag * out;
    }
const LL maxn = 100019 << 2, inf = 0xfffffffffffffff;
LL head[maxn],nume = 1;
struct Node{
    LL v,dis,nxt;
    }E[maxn << 3];
void add(LL u,LL v,LL dis){
    E[++nume].nxt = head[u];
    E[nume].v = v;
    E[nume].dis = dis;
    head[u] = nume;
    }
LL num, nr, s;
#define lid (id << 1)
#define rid (id << 1) | 1
LL tot;
struct seg_tree{
	LL l, r;
	LL Index[2];
	}tree[maxn << 2];
void build(LL id, LL l, LL r){
	tree[id].l = l, tree[id].r = r;
	if(l == r){
		tree[id].Index[0] = tree[id].Index[1] = l;
		return ;
		}
	tree[id].Index[0] = ++tot;//入边
	tree[id].Index[1] = ++tot;//out
	LL mid = (l + r) >> 1;
	build(lid, l, mid), build(rid, mid + 1, r);
	add(tree[id].Index[0], tree[lid].Index[0], 0);
	add(tree[id].Index[0], tree[rid].Index[0], 0);
	add(tree[lid].Index[1], tree[id].Index[1], 0);
	add(tree[rid].Index[1], tree[id].Index[1], 0);
	}
void IG(LL id, LL u, LL dis, LL l, LL r, LL o){//0 --> in, 1 --> out
	if(tree[id].l == l && tree[id].r == r){
		if(o == 2)add(u, tree[id].Index[0], dis);
		else add(tree[id].Index[1], u, dis);
		return ;
		}
	LL mid = (tree[id].l + tree[id].r) >> 1;
	if(mid < l)IG(rid, u, dis, l, r, o);
	else if(mid >= r)IG(lid, u, dis, l, r, o);
	else IG(lid, u, dis, l, mid, o), IG(rid, u, dis, mid + 1, r, o);
	}
void init(){
	num = RD(), nr = RD(), s = RD();
	tot = num;
	build(1, 1, num);
	REP(i, 1, nr){
		LL cmd = RD(), u = RD();
		if(cmd == 1){
			LL v = RD(), dis = RD();
			add(u, v, dis);
			}
		else{
			LL l = RD(), r = RD(), dis = RD();
			IG(1, u, dis, l, r, cmd);
			}
		}
	}
LL d[maxn];
bool vis[maxn];
void Djs(LL s){
	REP(i, 1, tot)d[i] = inf;
	priority_queue<pair<LL, LL> >Q;
	d[s] = 0;
	Q.push(make_pair(-d[s], s));
	while(!Q.empty()){
		LL u = Q.top().second;Q.pop();
		if(vis[u])continue;
		vis[u] = 1;
		for(LL i = head[u];i;i = E[i].nxt){
			LL v = E[i].v, dis = E[i].dis;
			if(d[u] + dis < d[v]){
				d[v] = d[u] + dis;
				Q.push(make_pair(-d[v], v));
				}
			}
		}
	}
void solve(){
	Djs(s);
	REP(i, 1, num){
		if(d[i] == inf)printf("-1 ");
		else printf("%lld ", d[i]);
		}
	puts("");
	}
int main(){
	init();
	solve();
	return 0;
	}