HDU_5563Clarke and five-pointed star

Clarke and five-pointed star

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 156    Accepted Submission(s): 88

Problem Description

Clarke is a patient with multiple personality disorder. One day, Clarke turned into a learner of geometric. 
When he did a research with polygons, he found he has to judge if the polygon is a five-pointed star at many times. There are 5 points on a plane, he wants to know if a five-pointed star existed with 5 points given.

 

Input

The first line contains an integer T(1≤T≤10), the number of the test cases. 
For each test case, 5 lines follow. Each line contains 2 real numbers xi,yi(−109≤xi,yi≤109), denoting the coordinate of this point.

 

Output

Two numbers are equal if and only if the difference between them is less than 10−4. 
For each test case, print Yes if they can compose a five-pointed star. Otherwise, print No. (If 5 points are the same, print Yes. )

 

Sample Input

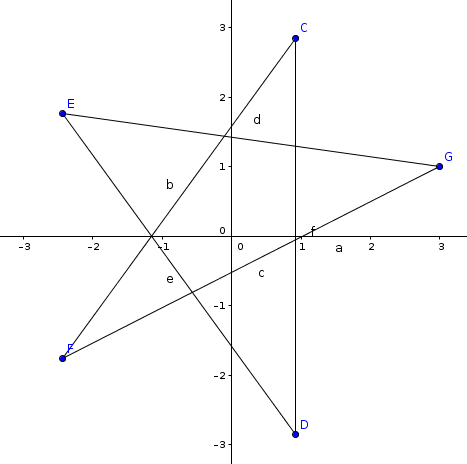
2
3.0000000 0.0000000
0.9270509 2.8531695
0.9270509 -2.8531695
-2.4270509 1.7633557
-2.4270509 -1.7633557
3.0000000 1.0000000
0.9270509 2.8531695
0.9270509 -2.8531695
-2.4270509 1.7633557
-2.4270509 -1.7633557

 

Sample Output

Yes
No

Hint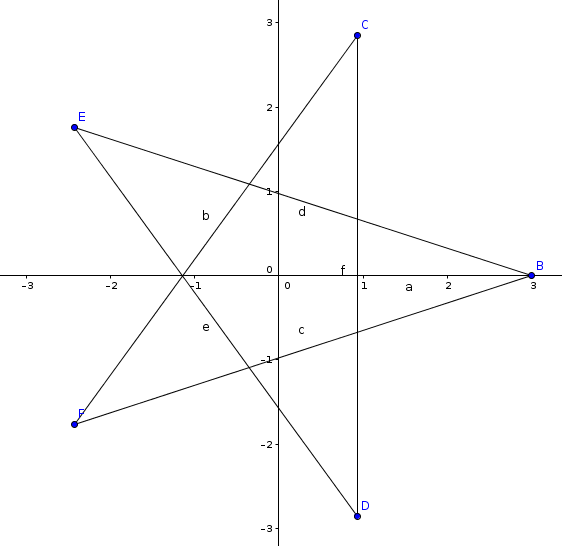


 
/*
  *题目大意：给你五个点的坐标、要求判断是否可以组成五角星 
 *算法分析：注意在五点相同时候为YES，否则判断是否存在有两组五条相等的边， 存在则YES，否则NO 
*/

#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
#include <cstdlib>
#include <cmath>
#include <algorithm>
using namespace std;

struct node{
	double x, y;
}a[5];

int panDuan(double a, double b) {
	if (fabs(a-b)<=1e-4)
		return 1;
	return 0;
}

double juLi(double x1, double y1, double x2, double y2) {
	return (double)(x1-x2)*(x1-x2) + (y1-y2)*(y1-y2);
}

int main() {
	int t;
	cin >> t;
	while (t --) {
		int flag = 0;
		memset(a, 0, sizeof(a));
		for (int i = 0; i<5; i++)
			cin >> a[i].x >> a[i].y;
		for (int i = 0; i<4; i++) {
			if (panDuan(a[i].x, a[i+1].x) == 0 || panDuan(a[i].y, a[i+1].y) == 0)
				flag = 1;
		}
		if (flag == 0)
			cout << "Yes" << endl;
		else {
			flag = 0;
			double ans1;
			double ans = juLi(a[0].x, a[0].y, a[1].x, a[1].y);
			for (int i = 0; i<5; i++) {
				for (int j = i+1; j<5; j++) {
					if (fabs(juLi(a[i].x, a[i].y, a[j].x, a[j].y) - ans) > 1e-4)
						ans1 = juLi(a[i].x, a[i].y, a[j].x, a[j].y);
				}
			}
			int flag1 = 0;
			//cout << ans << endl<< endl;
			for (int k = 0; k<5; k++) {
				for (int l = k+1; l<5; l++) {
					//cout << juLi(a[k].x, a[k].y, a[l].x, a[l].y) << endl << endl;
					if (panDuan(juLi(a[k].x, a[k].y, a[l].x, a[l].y), ans) == 1)
						flag ++ ;
					if (panDuan(juLi(a[k].x, a[k].y, a[l].x, a[l].y), ans1) == 1)
						flag1 ++ ;
				}
			}
			//cout << flag << endl;
			if (flag == 5 && flag1 == 5)
				cout << "Yes" << endl;
			else
				cout << "No" << endl;
		}
	}
	
	return 0;
}