优先队列（堆实现）

优先队列由二叉堆实现是很普遍的事情。

下面我把二叉堆也称作为堆。

堆是一棵被完全填满的二叉树，一棵高为h的二叉树2^h到2^h+1-1个节点。这意味着完全二叉树的高时log N。

因为完全二叉树很有规律，所有它可以用一个数组来表示，而不需要指针

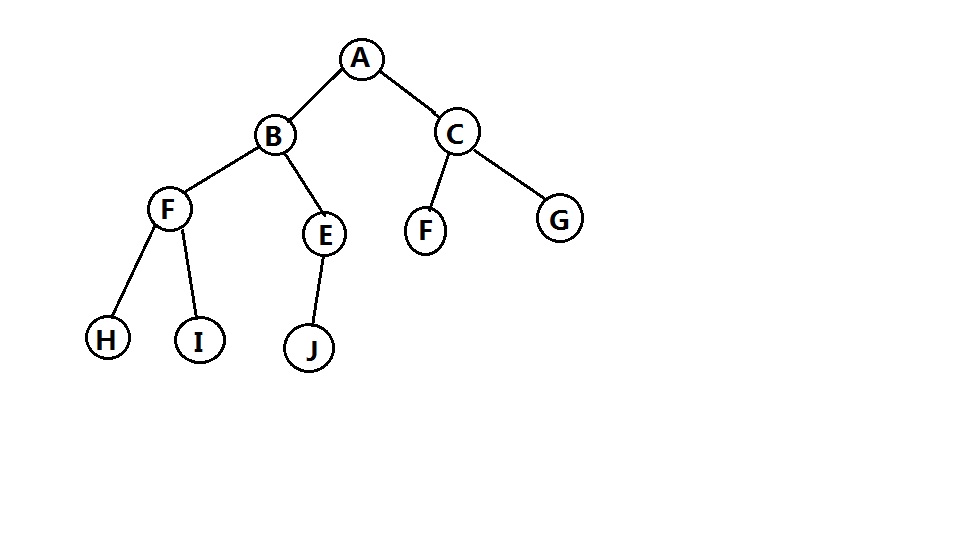
对于这棵树，我们可以这样表示。

　　

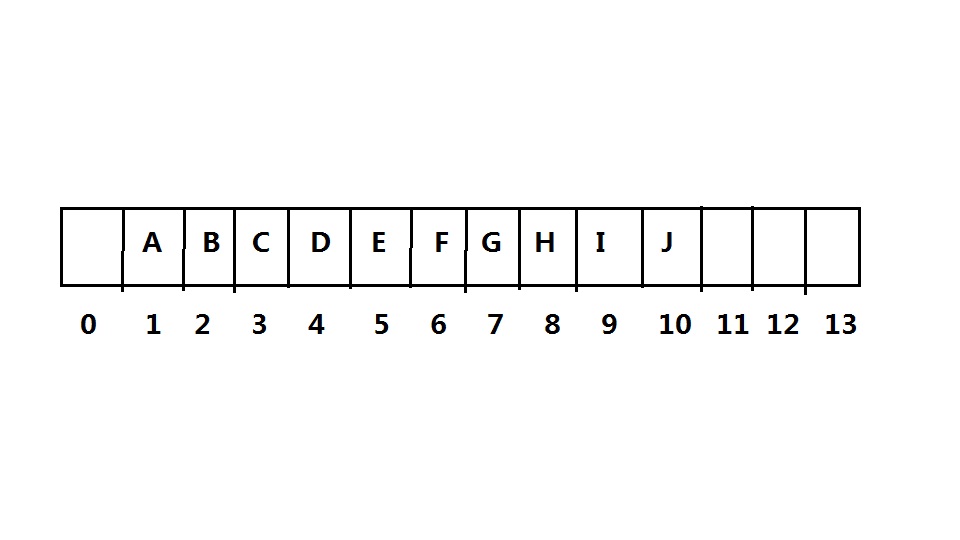
对于数组中任意一个位置 i 上的元素，其左儿子在位置 2 i 上，右儿子在左儿子后的单元（2 i + 1 ）,它的父亲则在位置（ i / 2 ）上。

#ifndef _BinHeap_H

struct HeapStruct;

typedef int ElementType

typedef struct HeapStruct *PriorityQueue;

PriorityQueue Initialize (int MaxElenments);

void Destroy(PriorityQueue H);

void MakeEmpty(PriorityQueue H);

void Insert(ElementType X,PriorityQueue H);

ElementType DeleteMin(PriorityQueue H);

ElementType Find(PriorityQueue H);

int IsEmpty(PriorityQueue H);

int Is Full (PriorityQueue H);


#endif // _BinHeap_H

struct HeapStruct{
    int Capacity;
    int Size;
    ElementType *Elements;
};

//对堆进行初始化
PriorityQueue Initialize(int MaxElements)
{
    PriorityQueue H;
    
    if(MaxElements < MinPQsize)
        Error("Priority queue size is too small");
    
    H = malloc(sizeof( struct HeapStruct));   //H等于HeapStruct的内存大小，malloc是向系统申请一个内存空间。
    if(H == NULL)
        FatelError ("Out of space!!!");
    H->Elements = malloc((MaxElements+1)*sizeof(ElementType));  //申请一个内存空间，之后就可以像数组一样对Elements进行操作。
    

    if(H->Elements == NULL)
        FatalError("Out of space!!!");   //H没有子节点了。
    
    H->Capacity = MaxElements;
    H->Size = 0;
    H->Elements[0] = MinDate
    
    return H;
}

// 插入元素

void Insert(ElementType X, PriorityQueue H )
{
    int i;
    if(IsFull(H))
    {
        Error("Priority queue is full");
        return ;
    }
    for(int i = ++H->Size;H->Elements[i/2]>X;i /= 2)   //采用冒泡，一个冒上去。
        H->Elements[i] = H->Elements[i/2];    //如果它比它的父亲节点小的话，那么冒泡上去。
    H->Elements[i] = X;
} 

//删除最小值

ElementType DeleteMin( PriorityQueue H )
{
    int i,Child;
    ElemenType MinElement , LastElement;
    
    if(IsEmpty( H ))
    {
        Error("Priority queue is empty");
        return H->Elements[ 0 ];
    }
    MinElement = H->Elements[ 1 ];
    LastElement = H->Elements[ H->Size-- ];
    
    for( i = 1;i * 2 <= H->Size; i = Child )     //将每一个子节点的最小值上升到原来的父亲节点。
    {
        Child = i * 2;
        if( Child != H->Size && H->Elements[ Child+1 ]
                             <  H->Elements[ Child ] )
            Child++;
        
        if( LastElement > H->Elements[ Child ])
            H->Elements[i] = H->Elements[ Child ];
        else 
            break;
    }
    H->Elements[ i ] = LastElement;
    return MinElement; 
    
}

自己写的便于套用的一个堆

int arr[]

void inset(int x,int y)
{
    int i;
    for(i = y; arr[ i / 2 ] > x;i /= 2)
        arr[ i ] = arr[ i / 2 ];
    arr[ i ] = x;
}

int deleteMin(int x)
{
    int i, child;
    int Min,last;
    Min = arr[1],last = arr[ x ];
    for(i = 1; i * 2 <= x; i = child )
    {
        child = i * 2;
        if( child != x && arr[ child+1 ]
                        < arr[ child ] )
            child++;
        if(last > arr[ child ])
            arr[ i ] = arr[ child ];
        else
            break;
    }

    arr[ i ] = last;
    return Min;
}