You are given two lists of non-zero digits.
Let's call an integer pretty if its (base 10) representation has at least one digit from the first list and at least one digit from the second list. What is the smallest positive pretty integer?
The first line contains two integers n and m (1 ≤ n, m ≤ 9) — the lengths of the first and the second lists, respectively.
The second line contains n distinct digits a1, a2, ..., an (1 ≤ ai ≤ 9) — the elements of the first list.
The third line contains m distinct digits b1, b2, ..., bm (1 ≤ bi ≤ 9) — the elements of the second list.
Print the smallest pretty integer.
2 3
4 2
5 7 6
25
8 8
1 2 3 4 5 6 7 8
8 7 6 5 4 3 2 1
1
In the first example 25, 46, 24567 are pretty, as well as many other integers. The smallest among them is 25. 42 and 24 are not pretty because they don't have digits from the second list.
In the second example all integers that have at least one digit different from 9 are pretty. It's obvious that the smallest among them is 1, because it's the smallest positive integer.
题意:找出两个数字,在两个数组都出现过,要求最小,注意,有可能只有一位。
#include <bits/stdc++.h> using namespace std; int a[10]; int b[10]; int main() { int n,m; scanf("%d%d",&n,&m); for(int i = 0; i < n; i++) scanf("%d",&a[i]); for(int i = 0; i < m; i++) scanf("%d",&b[i]); sort(a,a+n); sort(b,b+m); if(a[0]==b[0]) { printf("%d ",a[0]); } else { bool flag = false; int ans = 100; for(int i = 0; i < n; i++) { for(int j = 0; j < m; j++) { if(a[i]==b[j]) { flag = true; ans = a[i]; break; } } if(flag) break; } if(flag) printf("%d ",ans); else printf("%d%d ",min(a[0],b[0]),max(a[0],b[0])); } return 0; }
You are given an array a1, a2, ..., an consisting of n integers, and an integer k. You have to split the array into exactly k non-empty subsegments. You'll then compute the minimum integer on each subsegment, and take the maximum integer over the k obtained minimums. What is the maximum possible integer you can get?
Definitions of subsegment and array splitting are given in notes.
The first line contains two integers n and k (1 ≤ k ≤ n ≤ 105) — the size of the array a and the number of subsegments you have to split the array to.
The second line contains n integers a1, a2, ..., an ( - 109 ≤ ai ≤ 109).
Print single integer — the maximum possible integer you can get if you split the array into k non-empty subsegments and take maximum of minimums on the subsegments.
5 2
1 2 3 4 5
5
5 1
-4 -5 -3 -2 -1
-5
A subsegment [l, r] (l ≤ r) of array a is the sequence al, al + 1, ..., ar.
Splitting of array a of n elements into k subsegments [l1, r1], [l2, r2], ..., [lk, rk] (l1 = 1, rk = n, li = ri - 1 + 1 for all i > 1) is k sequences (al1, ..., ar1), ..., (alk, ..., ark).
In the first example you should split the array into subsegments [1, 4] and [5, 5] that results in sequences (1, 2, 3, 4) and (5). The minimums are min(1, 2, 3, 4) = 1 and min(5) = 5. The resulting maximum is max(1, 5) = 5. It is obvious that you can't reach greater result.
In the second example the only option you have is to split the array into one subsegment [1, 5], that results in one sequence ( - 4, - 5, - 3, - 2, - 1). The only minimum is min( - 4, - 5, - 3, - 2, - 1) = - 5. The resulting maximum is - 5.
题意:给定一个数组,划分为k个区间,最大化,区间内最小的数字的最大值。有点绕。
k > 2 ans = maxx
k = 1 ans = minx
k==2 枚举
#include <bits/stdc++.h> using namespace std; const int maxn = 1e5+5; int a[maxn]; int d[maxn]; int d2[maxn]; int main() { // freopen("in.txt","r",stdin); int n,k; scanf("%d%d",&n,&k); for(int i = 0; i < n; i++) d[i] = d2[i] = 1e9+5; int maxx = -(1e9 + 5); int minx = 1e9 + 5; for(int i = 0; i < n; i++) { scanf("%d",&a[i]); minx = min(minx,a[i]); maxx = max(maxx,a[i]); } d[0] = a[0]; for(int i = 1; i < n; i++) { d[i] = min(d[i-1],a[i]); } d2[n-1] = a[n-1]; for(int i = n-2; i >=0; i--) { d2[i] = min(d2[i+1],a[i]); } if(k==1) { printf("%d ",minx); } else if(k>2) printf("%d ",maxx); else { if(a[0]==maxx||a[n-1]==maxx) printf("%d ",maxx); else { int ans = -(1e9+5); for(int i = 0; i < n-1; i++) { int tmp = max(d[i],d2[i+1]); ans = max(ans,tmp); } printf("%d ",ans); } } return 0; }
You are given several queries. In the i-th query you are given a single positive integer ni. You are to represent ni as a sum of maximum possible number of composite summands and print this maximum number, or print -1, if there are no such splittings.
An integer greater than 1 is composite, if it is not prime, i.e. if it has positive divisors not equal to 1 and the integer itself.
The first line contains single integer q (1 ≤ q ≤ 105) — the number of queries.
q lines follow. The (i + 1)-th line contains single integer ni (1 ≤ ni ≤ 109) — the i-th query.
For each query print the maximum possible number of summands in a valid splitting to composite summands, or -1, if there are no such splittings.
1
12
3
2
6
8
1
2
3
1
2
3
-1
-1
-1
12 = 4 + 4 + 4 = 4 + 8 = 6 + 6 = 12, but the first splitting has the maximum possible number of summands.
8 = 4 + 4, 6 can't be split into several composite summands.
1, 2, 3 are less than any composite number, so they do not have valid splittings.
题意:给定一个数字n,求最多可以由多少个合数相加组成。
分析:尽可能的用4去组合。
#include <bits/stdc++.h> using namespace std; int a[20] = {0,-1,-1,-1,1,-1,1,-1,2,1,2,-1,3,2,3,2}; int main() { int q; cin>>q; while(q--) { int n; scanf("%d",&n); if(n<=15) { printf("%d ",a[n]); continue; } int k = n%4; if(k==0) printf("%d ",n/4); if(k==1) { printf("%d ",(n-9)/4+1); } if(k==2) { printf("%d ",(n-6)/4+1); } if(k==3) { printf("%d ",(n-15)/4+2); } } return 0; }

UVA 920
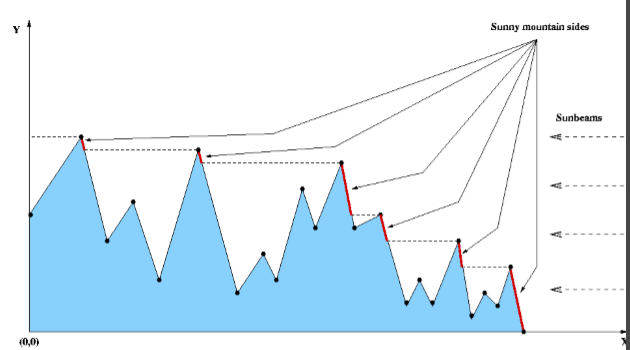
题目很形象,给定n个点坐标,从左往右的平行光线照射山峰,求图中红色的投影长度和。
分析:模拟照射过程,从右往左,只有下一个点较高的时候,才会有红色线段,而且此时的山峰不会再出现影子,维护一个尾部指针,指向当前可能产生影子的山峰,然后就是求影子长度了,投影长度和前一个点的角度有关,计算公式推导一下就行了。
#include <bits/stdc++.h> using namespace std; const int maxn = 105; struct Node { double x,y; bool operator < (const Node& rhs) const { return x < rhs.x; } }nodes[maxn]; int n; double dist(int i,int j) { double x = nodes[i].x - nodes[j].x; double y = nodes[i].y - nodes[j].y; return sqrt(x*x+y*y); } int main() { //freopen("in.txt","r",stdin); int t; scanf("%d",&t); while(t--) { scanf("%d",&n); for(int i = 0; i < n; i++) scanf("%lf%lf",&nodes[i].x,&nodes[i].y); sort(nodes,nodes+n); int last = n-1; double sum = 0; for(int i = n-2; i >=0; i--) { if(nodes[i].y>nodes[last].y) { sum += dist(i,i+1)*( (nodes[i].y-nodes[last].y)/ (nodes[i].y-nodes[i+1].y) ); last = i; } } printf("%.2lf ",sum); } return 0; }