因子分析的最后一步了,悲伤 !!!


在因子分析中,人们一般关注的重点是估计因子模型的参数(载荷矩阵),有时公共因子的估计(即所谓的因子得分)也是需要的,因子得分可以用于模型诊断,也可以作为下一步分析的原始数据。
需要指出的是,因子的得分计算并不是通常意义下的参数估计,他是对不可观测的随机变量 取值的估计
通常可以用加权最小二乘法和回归法来估计因子得分
栗子哥又来了


P252
我国上市公司赢利能力与资本结构的实证分析
这些公司的资本结构有 销售净利润,资产净利润,净资产收益率,销售毛利率,以及资产负利率
clc,clear; load ssgs.txt x = ssgs(:,[1:4]); y = ssgs(:,5); n = size(ssgs,1); % 数据标准化 求相关系数矩阵 x = zscore(x); r = corrcoef(x); % 进行主成分分析的相关计算,求旋转后的载荷矩阵 [vec1,val,con1] = pcacov(r); f1 = repmat(sign(sum(vec1)),size(vec1,1),1); vec2 = vec1.*f1; f2 = repmat(sqrt(val)',size(vec2,1),1); a = vec2.*f2;
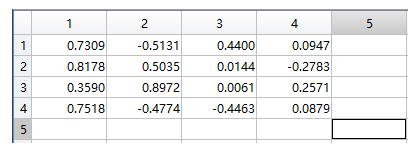

% 提出num个主因子的载荷矩阵 num = 2; am = a(:,[1:num]); % am 旋转变换,bm 为旋转后的载荷矩阵 [bm,t] = rotatefactors(am,'method','varimax');

% am 旋转变换,bm 为旋转后的载荷矩阵 [bm,t] = rotatefactors(am,'method','varimax'); % bt 前部分是旋转后的载荷矩阵 后部分为没有旋转的载荷矩阵 bt = [bm,a(:,[num+1:end])]; % 计算贡献因子 con2 = sum(bt.^2); % 可以查看一下旋转后的贡献率 check = [con1,con2'/sum(con2)*100]; % 旋转后的因子贡献率 rate = con2(1:num)/sum(con2);
计算得分函数的系数
% 计算得分函数的系数 coef = inv(r)*bm coef = 0.5060 -0.0450 0.1615 0.5151 -0.1831 0.5810 0.5015 -0.0199 % 计算各个因子得分 score = x*coef;
得分函数系数公式:


% 计算得分的权重 weight = rate/sum(rate); weight = 0.5163 0.4837

这个公式书上有问题的哦!!!


各个企业的得分:
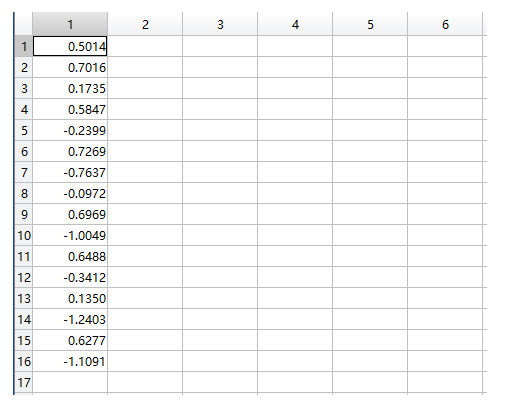

最后一步,对 F 继续利用,分析和 y 的回归方程:
% 计算因子 F 与 资产负债 y 的相关系数 [ccoef,p] = corrcoef([Tscore,y]); [d,dt,e,et,stats] = regress(Tscore,[ones(n,1),y]); d,stats d = 0.8290 -0.0268 stats = 0.4882 13.3524 0.0026 0.2745
得因子分析法的回归方程:
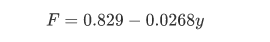
至此因子分析的5个步骤就全部完成了,也完成了变量内部联系的分析,和总体的一个评估,最后回忆一下过程:
-
数据标准化
-
相关系数矩阵
-
载荷矩阵
-
因子旋转
-
因子得分
恭喜大佬完成咯!!!
