我以前一直觉得AC自动机就是我打一个代码,然后可以帮我自动AC题目,现在才知道原来是处理字符串的一个有意思的东西,然后我们现在就来看一下这个东西
1464: [视频]【AC自动机】统计单词出现个数
时间限制: 1 Sec 内存限制: 128 MB
提交: 327 解决: 114
[提交] [状态] [讨论版] [命题人:admin]题目描述
【题意】
有n(n<=10000)个单词(长度不超过50,保证都为小写字母)和一句话(长度不超过1000000)
求出这句话包括几个单词
【输入格式】
输入t,表示有t组数据
每组数据第一行输入n,第i+1~i+n行输入n个单词,最后一行输入一句话
【输出格式】
输出这句话包括的单词个数(注意:一个单词重复出现,只算作出现了一个单词,如果有多个重复的单词,那么重复单词应该计算多次)
【样例输入】
1
5
she
he
say
shr
her
yasherhs
【样例输出】
3
首先把每一个单词建成一个字典树
如图:样例:
1
5
she
he
say
shr
her
yasherhs
黑色编号表示点的编号,黑色字母表示单词字符,下面是我们要处理的这句话这个时候引入一个新的知识:失败指针
这个失败指针是用来当我们匹配到一个点,发现不匹配时,我们所跳到的另一个点上,这个和KMP的p数组有一点点相似失败指针的定义:
如果i点的失败指针指向j的时候
s[i]表示从root到i点所构成的字符串
s[j]表示从root到j点所构成的字符串当j点为i点的失败指针时,满足s[j]为s[i]的后缀 (失败指针的定义一定要记住啊)
因为在字典树里面讲过,每个点都可以代表一个独立的单词(字符串)
比如说:如图
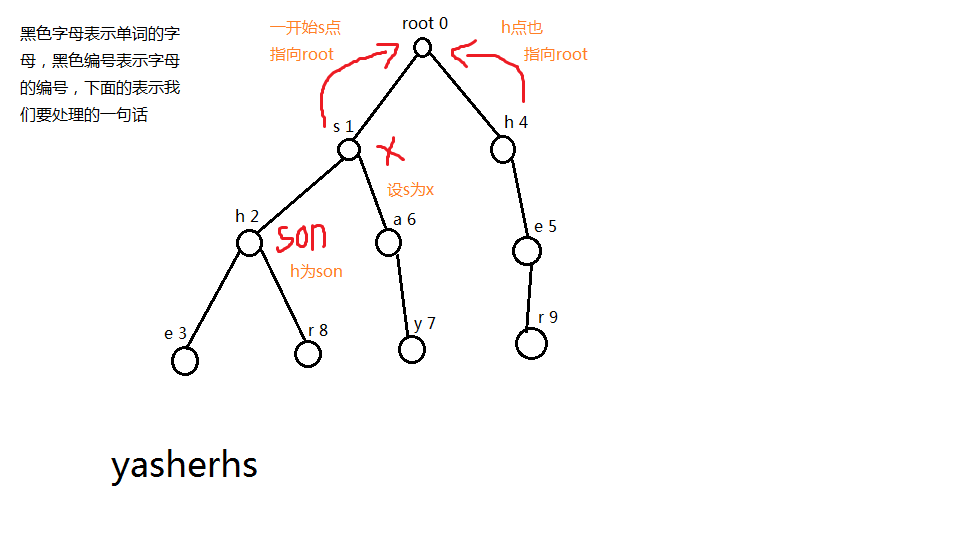
如果我们按照失败指针的操作的话,编号为2的h指向编号为4的h,因为从root到4号点所构成的字符串只有h一个,而从root到2号点所构成的字符串有sh两个,我们就可以看出h其实是sh的后缀,这个时候编号为2的h的失败指针就会指向编号为4的h,
注意:失败指针指向的那个点,因为我们一个点有可能会有很多个后缀,而有可能很多个后缀都在字典树里面出现过,这个指针指向的必定是所有当中满足条件的最长后缀
然后的话还是看代码的实现吧
因为我们提到了失败指针的概念,所以要在结构体当中定义一个fail,表示失败指针
又因为是多组数据,所以用一个clean函数来时时刻刻清空这棵字典树
还有一个bfs()函数,也就是宽搜,是用来构建失败指针的,
要定义一个优先队列,这个是用来存储我们失败指针的这个点的,优先队列只是一个队列,不会对我们插进去的队列进行操作,只是用来保存而已如果不存在,就继续找我的下一个指针,这个和KMP的思想是一样的,定义一个变量j来保存我们的失败指针
看图:
一开始s指向root,编号为4的h也指向root,然后我们看向编号为2的h,这个时候我们设s为x,编号为2的h为son,然后我们先去找x的失败指针,找到root这里,也就是0,如果=0,我们就会自动跳出搜索的while,tr[son].fail= max(tr[j].c[i],0);
看到这句话,为什么是max呢?因为有可能我匹配到root这个点的时候,root是不存在第i个孩子的,所以有可能这个tr[j].c[i]=-1,但是我们字典 树当中的所有点一但找不到适合的j点的时候,统统指向根,也就是0,假如他不是0,而且他又没有这个孩子的话,那么我们就继续找j的失败指针,其实我们在找j的失败指针的时候,j的失败指针也可以当作我x的失败指针,为什么呢?
因为我们在讲定义的时候,
如果i点的失败指针指向j的时候
s[i]表示从root到i点所构成的字符串
s[j]表示从root到j点所构成的字符串
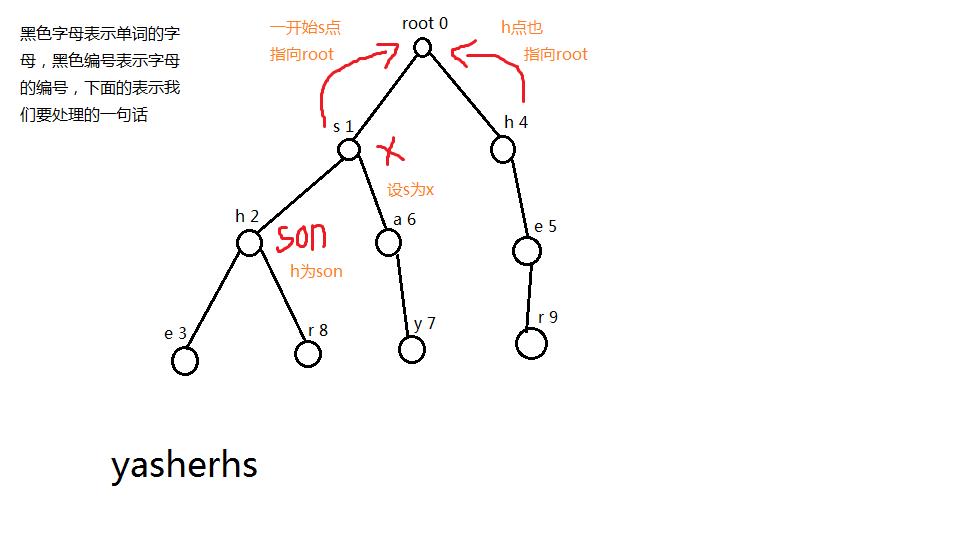
当j点为i点的失败指针时,满足s[j]为s[i]的后缀就比如说代码里面的j点,他的s[j]是满足s[x]的后缀的,那么s[j]这个假设j点的失败指针为k,那么s[k]为s[j]的后缀,然后s[j]又为s[x]的后缀,那么s[k]一定是s[x]的后缀,所以我们就可以直接用这一点来不断的更新的son的失败指针
然后我们每一次询问完之后,我们就把我们的孩子推进我们的优先队列里面,又因为我们的x已经操作完毕了,我们就从优先队列里面踢出来
但是我们在建树的时候,我们在每个单词的末尾那里,定义一个s,把s++表示这个点是一个单词的结尾
然后我们用solve来求出一个单词的解
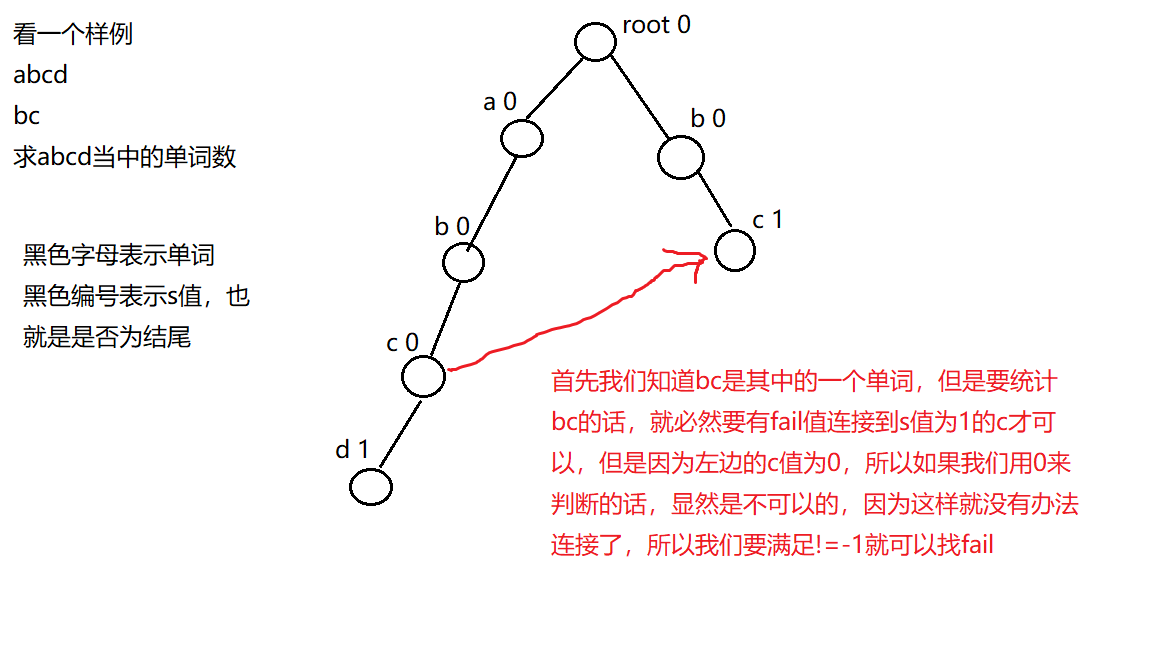
一开始x为根,假如当前x不为根,并且当前的x是没有y这个孩子的话,我们就找到x的失败指针,找完之后x就等于他的儿子,如果等于x=-1,就说明这个孩子不存在,那么就从根开始重新找,遍历到下一个字符,定义一个j是为了防止改变x的值,如果当前的这个点是一个单词的结尾或者多个单词的结尾,ans就记录下这个答案, 然后清零,因为已经使用过了,然后就找他的失败指针,重点在这里,我们的重点不是为了记录答案,而是为了找fail因为如果这个单词能够成立的话,那么我们的失败指针所指向的那个点所构成的字符串也是可以到达的,所以我们要找他的失败指针,也要加上他的单词数但是我们判断结尾的时候一定是不等于-1,而不是不等于0
如图
我有点不厚道的在上面就把代码实现的过程讲了一下,但是现在还是来看一下代码实现吧
(注释版,如果真的非常非常理解就不看注释版,不然的话就看一眼吧)

1 #include<cstdio> 2 #include<cstring> 3 #include<cstdlib> 4 #include<algorithm> 5 #include<cmath> 6 #include<iostream> 7 using namespace std; 8 char a[1000010]; 9 int tot,ans; 10 int list[1000010]; 11 struct node/*trie是字典树*/ 12 { 13 int s,fail,cnt[30];/*s表示单词的结尾,fail表示失败指针,cnt表示第几个孩子*/ 14 /* 15 失败指针的定义 16 如果i点的失败指针指向j的时候 17 s[i]表示从root到i点所构成的字符串 18 s[j]表示从root到j点所构成的字符串 19 当j点为i点的失败指针时,满足s[j]为s[i]的后缀 20 */ 21 node() 22 { 23 s=fail=0; 24 memset(cnt,-1,sizeof(cnt));/*初始化*/ 25 } 26 }tr[500010]; 27 void clean(int x)/*多组数据,每一次都要清空树*/ 28 { 29 tr[x].s=tr[x].fail=0; 30 memset(tr[x].cnt,-1,sizeof(tr[x].cnt)); 31 } 32 void build_tree(int root)/*建树,相当于字典树的建树,就是有一个小小的不一样的地方*/ 33 { 34 int x=root,len=strlen(a+1); 35 for(int i=1;i<=len;i++) 36 { 37 int y=a[i]-'a'+1;/*1~26*/ 38 if(tr[x].cnt[y]==-1) 39 { 40 tr[x].cnt[y]=++tot;/*新增加一个点*/ 41 clean(tot);/*将这个点的子树全部清空*/ 42 /*这样子就可以做到初始化的操作了*/ 43 } 44 x=tr[x].cnt[y]; 45 } 46 tr[x].s++;/*s++表示这个点是一个单词的结尾*/ 47 } 48 void bfs()/*宽搜,优先队列,用来存构造失败指针的点*/ 49 { 50 list[1]=0; int head=1,tail=1; 51 while(head<=tail) 52 { 53 int x=list[head]; 54 for(int i=1;i<=26;i++)/*从26个孩子开始*/ 55 { 56 int son=tr[x].cnt[i];/*son表示x的第i个孩子节点*/ 57 if(son==-1) continue;/*等于-1,代表我这个孩子不存在,找下一个孩子*/ 58 if(x==0) tr[son].fail=0; 59 /*如果x=0,就说明x是root,root所有孩子的失败指针都为0,因为是第一个字母, 60 所以不会有除了他本身和他匹配的点,所以他的失败指针都是指向root*/ 61 else 62 { 63 /*构造失败指针*/ 64 int j=tr[x].fail;/*j等于x的失败指针*/ 65 while(j!=0 && tr[j].cnt[i]==-1) j=tr[j].fail; 66 /*询问j的第i个孩子是否存在,假如不存在就继续找我们失败指针,这个和KMP的思想是差不多的 67 j=0也就是指向root就会自动跳出来*/ 68 69 /*假如他不是0,而且他又没有这个孩子的话,那么我们就继续找j的失败指针,其实我们在找j的失败指针的时候, 70 j的失败指针也可以当作我x的失败指针,为什么呢? 71 72 因为我们在讲定义的时候, 73 如果i点的失败指针指向j的时候 74 s[i]表示从root到i点所构成的字符串 75 s[j]表示从root到j点所构成的字符串 76 当j点为i点的失败指针时,满足s[j]为s[i]的后缀 77 78 就比如说代码里面的j点,他的s[j]是满足s[x]的后缀的,那么s[j]这个假设j点的失败指针为k,那么s[k]为s[j]的后缀, 79 然后s[j]又为s[x]的后缀,那么s[k]一定是s[x]的后缀,所以我们就可以直接用这一点来不断的更新的son的失败指针*/ 80 tr[son].fail=max(tr[j].cnt[i],0); 81 /*为什么是max呢?因为有可能我匹配到root这个点的时候,root是不存在第i个孩子的,所以有可能这个tr[j].c[i]=-1, 82 但是我们字典树当中的所有点一但找不到适合的j点的时候,统统指向根,也就是0*/ 83 } 84 list[++tail]=son;/*询问完毕就将孩子推进优先队列*/ 85 } 86 head++;/*x已经操作完毕,就踢出优先队列*/ 87 } 88 } 89 void solve() 90 { 91 int x=0; int len=strlen(a+1);/*一开始x为根*/ 92 for(int i=1;i<=len;i++) 93 { 94 int y=a[i]-'a'+1; 95 while(x!=0 && tr[x].cnt[y]==-1) x=tr[x].fail; 96 /*假如当前x不为根,并且当前的x是没有y这个孩子的话,我们就找到x的失败指针*/ 97 x=tr[x].cnt[y];/*找完之后x就等于他的儿子*/ 98 if(x==-1) {x=0; continue;}/*假如孩子不存在,就从根开始重新找*/ 99 int j=x;/*为了不改变x的值*/ 100 while(tr[j].s!=-1)/*如果这个是单词的结尾或者多个单词的结尾,就可以记录答案 101 这里为什么是-1而不是0呢?如图*/ 102 { 103 ans+=tr[j].s;/*记录答案*/ 104 tr[j].s=-1;/*因为我们已经用过了*/ 105 j=tr[j].fail;/*因为如果这个单词能够成立的话,那么我们的失败指针所指向的那个点所构成的字符串也是可以到达的, 106 所以我们要找他的失败指针,也要加上他的单词数*/ 107 } 108 } 109 } 110 int main() 111 { 112 int t; scanf("%d",&t); 113 while(t--) 114 { 115 int n; scanf("%d",&n); 116 ans=0; tot=0; clean(0); 117 for(int i=1;i<=n;i++) 118 { 119 scanf("%s",a+1); 120 build_tree(0);/*建树*/ 121 } 122 bfs();/*构造失败指针*/ 123 scanf("%s",a+1); 124 solve();/*寻找答案*/ 125 printf("%d\n",ans); 126 } 127 return 0; 128 }
(非注释版,我建议完全打懂了之后用这个来测试一下自己是不是真的懂)

1 #include<cstdio> 2 #include<cstring> 3 #include<cstdlib> 4 #include<algorithm> 5 #include<cmath> 6 #include<iostream> 7 using namespace std; 8 char a[1000010]; 9 int tot,ans; 10 int list[1000010]; 11 struct node 12 { 13 int s,fail,cnt[30]; 14 node() 15 { 16 s=fail=0; 17 memset(cnt,-1,sizeof(cnt)); 18 } 19 }tr[500010]; 20 void clean(int x) 21 { 22 tr[x].s=tr[x].fail=0; 23 memset(tr[x].cnt,-1,sizeof(tr[x].cnt)); 24 } 25 void build_tree(int root) 26 { 27 int x=root,len=strlen(a+1); 28 for(int i=1;i<=len;i++) 29 { 30 int y=a[i]-'a'+1; 31 if(tr[x].cnt[y]==-1) 32 { 33 tr[x].cnt[y]=++tot; 34 clean(tot); 35 } 36 x=tr[x].cnt[y]; 37 } 38 tr[x].s++; 39 } 40 void bfs() 41 { 42 list[1]=0; int head=1,tail=1; 43 while(head<=tail) 44 { 45 int x=list[head]; 46 for(int i=1;i<=26;i++) 47 { 48 int son=tr[x].cnt[i]; 49 if(son==-1) continue; 50 if(x==0) tr[son].fail=0; 51 else 52 { 53 int j=tr[x].fail; 54 while(j!=0 && tr[j].cnt[i]==-1) j=tr[j].fail; 55 tr[son].fail=max(tr[j].cnt[i],0); 56 } 57 list[++tail]=son; 58 } 59 head++; 60 } 61 } 62 void solve() 63 { 64 int x=0; int len=strlen(a+1); 65 for(int i=1;i<=len;i++) 66 { 67 int y=a[i]-'a'+1; 68 while(x!=0 && tr[x].cnt[y]==-1) x=tr[x].fail; 69 x=tr[x].cnt[y]; 70 if(x==-1) {x=0; continue;} 71 int j=x; 72 while(tr[j].s!=-1) 73 { 74 ans+=tr[j].s; 75 tr[j].s=-1; 76 j=tr[j].fail; 77 } 78 } 79 } 80 int main() 81 { 82 int t; scanf("%d",&t); 83 while(t--) 84 { 85 int n; scanf("%d",&n); 86 ans=0; tot=0; clean(0); 87 for(int i=1;i<=n;i++) 88 { 89 scanf("%s",a+1); 90 build_tree(0); 91 } 92 bfs(); 93 scanf("%s",a+1); 94 solve(); 95 printf("%d\n",ans); 96 } 97 return 0; 98 }