图像缩放算法（最临近点插值算法、双线性内插值算法、双立方插值算法）

1、最临近点插值算法：

　　当一张（N*M）大小的图像放大到（（j*N）*（k*M））时，那么两张图像之间的像素点存在对应关系：

X1max / N = X2max / ( j * N ) ; 
Y1max / M = Y2max / ( k * M ) ;

其中：X1max，Y1max为源图像中两个方向的像素个数；X2max,Y2max为放大之后的图像两个方向上的像素个数；

即可得到 j  k；

x1 = x2 / j
y1 = y2 / k

放大之后（x2，y2）的像素信息按照上述公式，即可得到其对应的在源图像中的像素点，然后将原图像上的像素信息复制到（x2，y2）；

如果得到的x1，y1不为整数，将其四舍五入为一个整数，

假设有一张3×3大小的图像:

234	38	22
67	44	12
89	65	63

将其放大到4×4：

234	38	22	22
67	44	12	12
89	65	63	63
89	65	63	63

优点：占用内存小；缺点：放大之后的图像有明显的锯齿，缩小失真；就是简单的将原图像中的像素信息简单的copy到新的图像中

2、双线性内插值算法

　　与临近点插值算法的直接把原图像像素信息copy相比，双线性内插值算法是将得到的原采样点（浮点数）的附近点的四个像素点像素信息乘以权重得到新图像的像素信息；

将临近点插值算法中得到的x1（x1=j+t），y1（x1=k+u）,其中，j k是整数部分；t u 是小数部分；

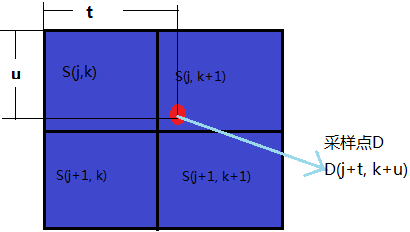
根据水平方向 t  计算出四个像素的权重。

Q11 = S(j,k) * (1-t) + S(j, k+1) * t;

Q22 = S(j+1, k) * (1-t) + S(j+1,K+1) *t

利用Q11, Q22的值，进行垂直方向权重计算得出计算采样点值

D(x, y) = Q11*(1-u) + Q22 * u; 把Q11, Q22带入,最终有等式:

D(x, y) = S(j, k) *(1-t)*(1-u) + S(j, k+1)*t*(1-u) + S(j+1,k)*(1-t)*u + S(j+1,k+1)*t*u

从而得出四个对应的权重系数分别为:

a = (1-t)*(1-u)

b = (1-t)*u

c = t*u

d = t*(1-u)

带入公式一，即可得出目标像素的值。

优点：可以有效的抗锯齿；缺点：算法没有考虑边缘和图像的梯度变化

3、双立方插值算法