【bzoj 4407】于神之怒加强版

Description

给下N,M,K.求

 

 

Input

输入有多组数据，输入数据的第一行两个正整数T,K，代表有T组数据，K的意义如上所示，下面第二行到第T+1行，每行为两个正整数N,M，其意义如上式所示。

Output

如题

Sample Input

1 2
3 3

Sample Output

20

HINT

1<=N,M,K<=5000000,1<=T<=2000

题解：

（若因博客园导致数学公式重叠，建议Ctrl+滑轮，重新缩放）

$ans=sum_{i=1}^{n}sum_{j=1}^{m}gcd(i,j)^{k}$

$=sum_{d=1}^{n}d^{k}sum_{i=1}^{lfloor frac{n}{d} floor}sum_{j=1}^{lfloor frac{m}{d} floor}[gcd(i,j)==1]$

$=sum_{d=1}^{n} d^{k}sum_{k=1}^{lfloor frac{n}{d} floor}mu(k)lfloorfrac{n}{kd} floorlfloorfrac{m}{kd} floor$

$=sum_{T=1}^{n}lfloor frac{n}{T} floorlfloor frac{m}{T} floorsum_{d|T}mu(frac{T}{d})d^{k}$

再设：$g(T)=sum_{d|T}mu(frac{T}{d})d^{k}$

当T是质数时

$g(T)=T^{k}mu(1)+1^{k}mu(T)=T^{k}-1$

当i与p互质时

对于$g（i）$约数的每个枚举其内部多了$g(p)$的约数枚举

$ herefore g(i*p)=g(i)*g(p)$

当i与p不互质时

首先$i=p^{x}*t$

由莫比乌斯函数定义可知，对g(i)存在贡献的d中至少含有x-1个p

因此在$g(i*p)$的枚举中，每个数值d（i*p）都对应着$g(i)$中的一个枚举数值d（i）满足：
$d(i*p)=d(i)*p$

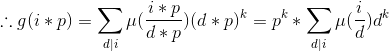
$                 =g(i)*p^{k} $

然后分块+线筛即可