loading……
以下为正文：
======================================================================================
序：最近被反演虐的不要不要的，遂决定写一篇博文，防止以后自己翻车……
1.定义
莫比乌斯函数：$mu(n)$
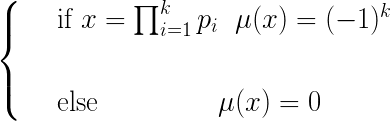
我们引入一个概念，狄利克雷卷积。即$（f*g）(n)=sum_{d|n}f(d)*g(frac n d)$。显然，狄利克雷卷积是满足交换律的。同时其也满足结合律与分配率。
在引入一个概念，积性函数，即函数$f$对于互质的两个数$i，j$满足$f(i*j)=f(i)*f(j)$。其中如果对于任意$i,j$满足$f(i*j)=f(i)*f(j)$，我们称其为完全积性函数。
再例举一些函数的符号：欧拉函数$phi$，约数个数函数$d$，约数和函数$sigma$，单位函数$id(n)=n$，元函数$varepsilon(n)$,当n为1时，$varepsilon(n)=1$，否则$varepsilon(n)=0$，以及不变的函数$1(n)=1$。
这里给出一个线性筛的板子：
1 const int N=1e7+1; 2 3 int miu[N],prim[N/5],num,sum[N]; 4 bool vis[N]; 5 6 inline void init(){ 7 miu[1]=1; 8 sum[1]=1; 9 for(int i=2;i<N;i++){ 10 if(!vis[i]) 11 prim[++num]=i,miu[i]=-1; 12 for(int j=1;prim[j]*i<N;j++){ 13 vis[i*prim[j]]=1; 14 if(i%prim[j]==0){ 15 miu[i*prim[j]]=0; 16 break; 17 } 18 miu[i*prim[j]]=-miu[i]; 19 } 20 sum[i]=sum[i-1]+miu[i]; 21 } 22 }
2.莫比乌斯函数的性质
这一段是从目前做过的题总结的，以后没准还得改（没准写的不够……）
莫比乌斯函数一个十分总要的性质，即$(mu *1)(n)$当且仅当$n==1$时，为1，否则为0。
关于这个的证明用 二项式定理+唯一分解定理 是很好证明的，这里就不多说了。
3.莫比乌斯反演
关于这块，一来是式子太长，二来是百度已经写得很全面了，所以蒟蒻就不献丑了。
参考链接：百度百科。
我想，这里比较重要的一个性质是：$F(n)=(f*1)(n)$，若$f$为积性函数，则$F(n)$也是积性函数。
证明如下：
设$gcd (n,p)==1$。
$F(n*p)=sum_{i|n}sum_{j|p}f(i*j)=sum_{i|n}f(i)sum_{j|p}f(j)=F(n)*F(p)$
证毕。
这个性质在我们反演出一个形如$ans=sum_{i=1}^{n}g(i)sum_{d|i}f(d)$的式子时，若$f$为积性函数，则我们可以将这个式子时间复杂度优化到至少$O(n)$。
例如：
$$F(n)=sum_{i|n}mu(i)*i*n$$
4.一些小证明：
身边大佬们总是在思考一些小证明，所以我也补补emmmm
顺便发一下网上的LaTeX(博客园真的是……)
(1)
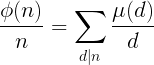，就是绿皮上辣个智障式子。换一下形式其实就是$phi=(mu*1)$。证明如下：
(2)
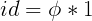。emmmmm虽然很弱，还是证一下吧：
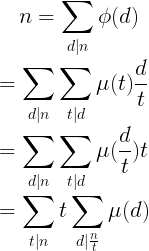
emmmm，然后当且仅当$frac{n}{t}==1$时，后面的$sum_{d|frac{n}{t}}mu(d)$为1，否则为0。证毕。
话说其实（1）里面那个式子由mobius反演就能证明emmmmmm
5.一些奇奇怪怪筛法
1）最小质因数筛法：
我们在筛某个函数$F$的时候，往往其并不是一个正常的积性函数，假设当前枚举数字为$i$，所用质数为$p$，我们一般会进行关于i与p的关系进行分类讨论，并且会用到$i$将$p$除尽的后得到的$j$，若一直除的话筛法就不再是线性，为了保证线性，我们就要用到最小质因数。
假设$prime$为$i$的最小质因数，显然在通常的线筛中我们知道若枚举的质数$p$满足$p<prime$则会枚举下一个质数，否则$break$，那么我们利用这一点，假设我们已经得到了$i$的最小质因数$prime$以及其次方项，当前枚举质数为$p$，那么对于计算到的$i*p$，当$p<prime$时直接按照$(i，p）==1$的情况讨论，同时显然可以知道$i*p$的最小质因数要跟新为$p$；当$p==prime$时，则按照$(i,p)==p$的情况讨论，由于我们已经记录了$i$的最小质因数$prime$以及其次方，我们可以直接$O(1)$得出其对应的$j$，同时对于$i*p$的最小质因数次数加1。
这样就维持了$O(n)$的线性筛。例子：BZOJ 3309 DZY love math
2）一类关于质数$p$成多项式的积性数论函数的筛法
6.关于做题
这个我也没有什么发言权，毕竟我太弱了……但还是想总结一下自己的想法。
反演最重要的是$gcd(i,j)==1$等价为$sum_{d|t}mu(d),t=gcd(i,j)$这一式子，在目前所遇到的题目中，关键都是如何将题目给出的内容转化为$gcd$，并且正确的化解，这个我也不怎么会，只能多练习了。
7.总结
个人觉得一些基本证明会不会都不是很重要，毕竟也不可能考为什么$id=(phi*1)$之类的，明白其过程，对思考有启发就足以。
8.一些题目：
BZOJ YY的GCD
BZOJ 4176 Lucas的数论
BZOJ 3930 CQOI2015 选数
bzoj2693: jzptab
BZOJ 4174 tty的求助
BZOj 3601：一个人的数论