「CodeChef Dec13 REALSET」 Petya and Sequence 循环卷积

题目大意：

　　传送门

　　T组询问。

　　每组给一个数组，询问该数组是否循环移位线性无关，输出YES或NO。

题解：

　　LCA冬令营有讲……然而当时……

　　并不知道如何计算一个数组是否循环移位线性无关……网上也没有……学校还加了白名单，翻不了墙，看不了wiki（英文看不懂……）。所以这就是我怂题解的理由23333。

　　题解上说wiki上循环矩阵的行列式等于其DFT后点值乘积。即对于矩阵：

　　

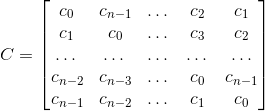
　　有：

　　

　　显然如果循环数组的矩阵的轶不为n的话其行列式必然为0。

　　所以把数组DFT以后看一下其乘积是否为0即可。

　　证明什么的……留个坑吧。

　　看到了一个大神打了几十行……没看懂在干什么……

　　LCA说还可以用分圆多项式，然而并没有找到资料。再留个坑吧……

代码：

#include "bits/stdc++.h"
 
using std::swap;
 
inline int read () {
    int s=0,k=1;char ch=getchar();
    while (ch<'0'|ch>'9') ch=='-'?k=-1:0,ch=getchar();
    while (ch>47&ch<='9') s=s*10+(ch^48),ch=getchar();
    return s*k;
}
 
typedef long long ll;
 
const int N=1e5+10;
 
ll mod,g,w[2][N],W[2][N],n,m;
 
inline ll gcd (ll a,ll b) {
    return b?gcd(b,a%b):a;
}
 
inline ll Mult ( ll a,ll b ) {
    return ( a*b - (ll)( (long double) a*b/mod )*mod + mod )% mod;
}
 
inline ll powmod ( ll a, ll b ) {
    ll ret=1;
    while (b) {
        if (b&1) ret=Mult ( ret, a );
        b>>=1,a=Mult ( a, a);
    }return ret;
}
 
inline int is_prim(ll x) {
    for (int i=2;1ll*i*i<=x;++i)
        if (x%i==0) return false;
    return true;
}
 
inline int is_prim_root(ll x,ll y){
    for (int i=1;1ll*i*i<y;++i)
        if ((y-1)%i==0) {
            if (powmod(x,i)==1) return false;
            if (powmod(x,(y-1)/i)==1)return false;
        }
    return true;
}
 
inline void init () {
    for (m=1;m<=2*n;m<<=1);
    ll lcm = n*m/gcd(n,m);
    mod = lcm + 1;
    for (int i=30;~i;--i)
        if (mod + (lcm<<i)<1e3*n) mod+=lcm<<i;
    while (mod<1e3*n) mod+=lcm;
    while (!is_prim(mod))  mod+=lcm;
    for (g=2;;++g) {
        int flag=true;
        for (int i=2;1ll*i*i<=mod;++i) if ((mod-1)%i==0){
            if (powmod(g,i)==1) {flag=false;break;}
            if (powmod(g,(mod-1)/i)==1) {flag=false;break;}
        }
        if (flag) break;
    }
    
    ll w0=powmod(g,(mod-1)/m);
    w[0][0]=w[1][0]=1;
    int i;
    for (i=1;i<m;++i) w[0][i]=Mult(w[0][i-1],w0);
    for (i=1;i<m;++i) w[1][i]=w[0][m-i];
    w0=powmod(g,(mod-1)/n);
    W[0][0]=W[1][0]=1;
    for (i=1;i<n;++i) W[0][i]=Mult(W[0][i-1],w0);
    for (i=1;i<n;++i) W[1][i]=W[0][n-i];
}
 
 
inline void NTT(ll *a,int n,int f) {
    register int i,j,k,l,t;
    for (i=j=0;i^n;++i) {
        if (i>j) std::swap(a[i],a[j]);
        for (k=n>>1;(j^=k)<k;k>>=1);
    }
    for (i=1;i<n;i<<=1) 
        for (j=0,t=n/(i<<1);j<n;j+=i<<1) 
            for (k=l=0;k<i;++k , l+=t ) {
                ll x=a[j+k],y=Mult(a[i+j+k],w[f][l]);
                a[j+k]=x+y;
                a[i+j+k]=x-y;
                if (a[j+k]>=mod) a[j+k]-=mod;
                if (a[i+j+k]<0) a[i+j+k]+=mod;
            }
    if (f ) {
        ll rev=powmod ( n,mod-2 );
        for (i=0;i<n;++i) a[i]=Mult(a[i],rev);
    }
}
 
 
inline void Bluesteins(ll *a,int f){
    static ll X[N],Y[N];
    register int i;
    for (i=0;i<2*n;++i) Y[2*n-1-i]=W[f][1ll*i*(i-1)/2%n];
    for (i=2*n;i<m;++i) Y[i]=0;
    NTT(Y,m,0);
    for (i=0;i<n;++i) X[i]=Mult(a[i],W[f][ (n-1ll*i*(i-1)/2%n)%n ]);
    for (i=n;i<m;++i) X[i]=0;
    NTT(X,m,0);
    for (i=0;i<m;++i) X[i]=Mult(X[i],Y[i]);
    NTT(X,m,1);
    for (i=0;i<n;++i)
        a[i]=Mult (X[2*n-1-i],W[f][(n-1ll*i*(i-1)/2%n)%n ]);
    if (f)  {
        ll rev=powmod(n,mod-2);
        for (i=0;i<n;++i) a[i]=Mult(a[i],rev);
    }
}

ll a[N];
 
int main (int argc, char const* argv[]){    
    //freopen("Dec13Realset.in","r",stdin);
    int T=read(),i;
    while (T-- ){
        n=read();
        for (i=0;i<n;++i) a[i]=read();
        init();
        Bluesteins(a,0);
        ll flag=1;
        for (i=0;i<n;++i) flag=Mult(flag,a[i]);
        puts(flag?"NO":"YES");
    }
    return 0;
}