关路灯题解

又是一道dp题，普及+还是费了我一中午，写篇题解吧；

题目

题目明确指出走到一个点之后的选择是可以有两种，要么向左走，要么向右走；花费长路程关掉功率大的灯可能是比关掉功率小但是近的灯花费少的；这一点很容易被证明；

所以我们可用将dp[i][j]加上一维[k],表示发生状态转移时，位于左端点（k=0）还是右端点（k=1）的花费，sum表示功率前缀和；

本校oj（N<=1000）也是可以过的；

那么对于dp[i][j][1]可以由两种状态转移得来：

dp[i][j][0]=min(dp[i+1][j][0]+cost(i,i+1,i,j),dp[i+1][j][1]+cost(i,j,i,j));
dp[i][j][1]=min(dp[i][j-1][0]+cost(i,j,i-1,j-1),dp[i][j-1][1]+cost(j-1,j,i-1,j-1))；

cost函数呢：（return (D[y]-D[x])*(sum[xx]+sum[n]-sum[yy]);）

我来解释一下怎么推出来cost函数；

首先时间一定是（d[j]-d[i]）了，那么是哪些灯亮着呢；

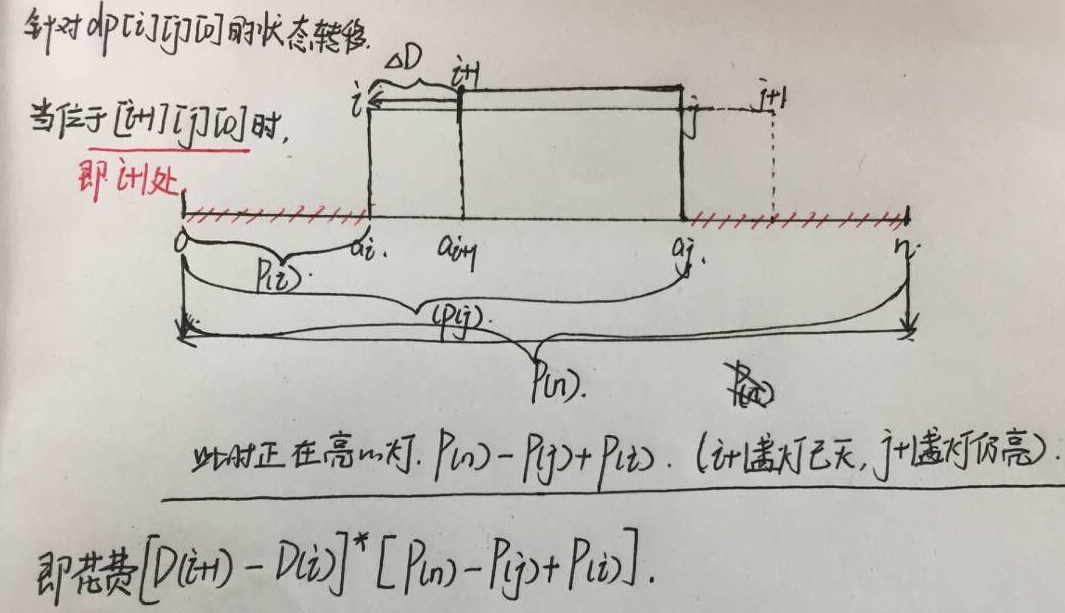
因为在这时，只有红色部分的灯是亮者的，这里只分析了对于其中一种情况的一种，另外三种也能推出来，这是我自己的理解，历史课上偷偷画的；

针对枚举的循环，因为要更新dp[i][j][0]的信息时，我们要知道dp[i+1][j][0],dp[i+1][j][1];对于dp[i][j][1]，j-1对应的状态要已知，所以j正着，i倒着做；

好了，看代码：

#include<bits/stdc++.h>
using namespace std;
template<typename T>inline void read(T &x)
{
    x=0;T f=1,ch=getchar();
    while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();}
    while(isdigit(ch))  {x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
    x*=f;
}
int n,c,a,D[1010],sum[1010],dp[1010][1010][2];
inline int cost(int x,int y,int xx,int yy)  {
    return (D[y]-D[x])*(sum[xx]+sum[n]-sum[yy]);
}
int main() {
    read(n);read(c);
    memset(sum,0,sizeof(sum));
    for(int i=1;i<=n;i++) {
        read(D[i]);read(a);
        sum[i]=sum[i-1]+a;
    }
    memset(dp,0x3f,sizeof(dp));
    dp[c][c][0]=dp[c][c][1]=0;
    for(int j=c;j<=n;j++) {
        for(int i=j-1;i>0;i--) {
            dp[i][j][0]=min(dp[i+1][j][0]+cost(i,i+1,i,j),dp[i+1][j][1]+cost(i,j,i,j));
            dp[i][j][1]=min(dp[i][j-1][0]+cost(i,j,i-1,j-1),dp[i][j-1][1]+cost(j-1,j,i-1,j-1));
        } 
    }
    cout<<min(dp[1][n][1],dp[1][n][0])<<endl;
    return 0;
}