现在很多大型IT企业在面试时都喜欢问一些智力相关的题目,虽然智力面试题在面试笔试中占的比例不大,但很多时候,面试环节中智力题往往会成为我们拿offer的最大拦路虎。因为有些面试官认为通过智力题可以考查你的思维能力、抽象问题的能力。
题目1:
有一栋楼共100层,一个鸡蛋从第N层及以上的楼层落下来会摔破, 在第N层以下的楼层落下不会摔破。给你2个鸡蛋,设计方案找出N,并且保证在最坏情况下, 最小化鸡蛋下落的次数。(假设每次摔落时,如果没有摔碎,则不会给鸡蛋带来损耗)
在参考下面的解答之前,请你先仔细思考10分钟。看你给出的方案最小下落次数是多少。如果题目总分10分,看看自己能得几分。
解答1:得0分的答案
用二分法。
解答2:得5分的答案
将100层楼分成10分,每一份就是10层楼。首先,将鸡蛋从第10层楼开始扔。那么结果有两种可能:
情况1:如果碎了,说明临界楼层在1到10之间,但现在只剩下一个鸡蛋了,只能从第一层一直到第10层。
情况2:如果没有碎,接下来从第20层扔鸡蛋。
该方法的思路是,用一个鸡蛋来试探,找到临界楼层的大致范围[1~10]、[11-20]….[91-100]。然后用另一个鸡蛋在大致范围内找出精确楼层。该方法的最坏次数是:18次。
解答3:得10分的答案
假设问题存在最优解,这个最优解的最坏情况尝试次数是x次。那么,我们第一次扔鸡蛋恰恰应该选第x层。选择高一层或低一层都不合适
究竟为什么呢?下面分析一下
假设第一次扔在第x+1层:
如果第一个鸡蛋碎了,那么第二个鸡蛋只能从第1层开始一层一层扔,一直扔到第x层。
这样一来,我们总共尝试了x+1次,和假设尝试x次相悖。由此可见,第一次扔的楼层必须小于x+1层。
假设第一次扔在第x-1层:
如果第一个鸡蛋碎了,那么第二个鸡蛋只能从第1层开始一层一层扔,一直扔到第x-2层。
这样一来,我们总共尝试了x-2+1 = x-1次,虽然没有超出假设次数,但似乎有些过于保守。
假设第一次扔在第x层:
如果第一个鸡蛋碎了,那么第二个鸡蛋只能从第1层开始一层一层扔,一直扔到第x-1层。
这样一来,我们总共尝试了x-1+1 = x次,刚刚好没有超出假设次数。
因此,要想尽量楼层跨度大一些,又要保证不超过假设的尝试次数x,那么第一次扔鸡蛋的最优选择就是第x层。
如果第一次扔鸡蛋是在第x层,并且没有打碎,那么第二次扔鸡蛋是在哪一层呢?
由于第一次扔鸡蛋没有碎,尝试次数消耗一次,那么尝试次数不得超过x-1次,
尝试次数上限变成了x-1次,所以第二次尝试的楼层跨度也是x-1层,绝对楼层是x+x-1层
同理,如果鸡蛋还是没有碎,第三次楼层跨度是x-2,第四次x-3,第五次......
因此可以列出一个楼层数的方程式:
x + (x-1) + (x-2) + ... + 1 = 100
这个方程式不难理解:
左边的多项式是各次扔鸡蛋的楼层跨度之和。由于假设尝试x次,所以这个多项式共有x项。
右边是总的楼层数100。
下面我们来解这个方程:
x + (x-1) + (x-2) + ... + 1 = 100 转化为
(x+1)*x/2 = 100
最终x向上取整,得到 x = 14
因此,最优解在最坏情况的尝试次数是14次,第一次扔鸡蛋的楼层也是14层。
最后,让我们把第一个鸡蛋没碎的情况下,所尝试的楼层数完整列举出来:
14,27, 39, 50, 60, 69, 77, 84, 90, 95, 99, 100
举个例子验证下:
假如鸡蛋不会碎的临界点是65层,那么第一个鸡蛋扔出的楼层是14,27,50,60,69。这时候啪的一声碎了。
第二个鸡蛋继续,从61层开始,61,62,63,64,65,66,啪的一声碎了。
因此得到不会碎的临界点65层,总尝试次数是 6 + 6 = 12 < 14 。
题目2:64匹马,8个赛道,最少比几次找出跑得最快的4匹马
首先我们将64匹马分成48组,占用8个跑道,进行8个组的比赛,累计8次:
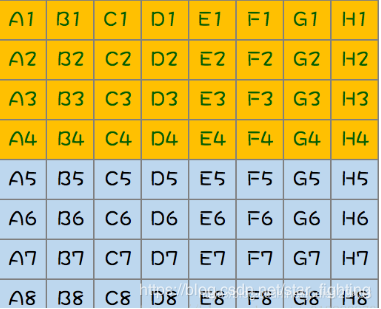
这里蓝色的视为淘汰的马,因为只需要我们算出最快的四匹马;
这个时候然后取8次跑的第一名进行比赛,然后淘汰掉后四名所在的组的所有马
因为,后四名所在的组的第一名没有跑过前四名的马,所以可以直接淘汰。累计9次
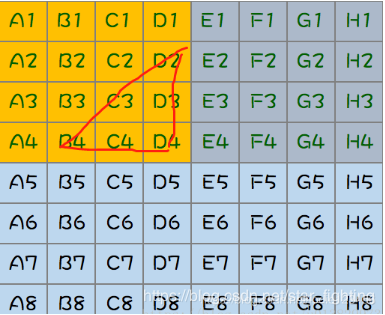
这个时候还可以进行淘汰,因为D1是a1,a2,a3之后的排名,所以d2,d3,d4可以淘汰,第四名也可能出现在C2中,C2是所在组的第二名,那么C3,C4也可以淘汰了,根据这样进行分析,可以得到B4也可以淘汰了;
这个时候你就会发现最快的一匹马A1已经出来了,然后随便选出一匹马,剩余的8匹马进行比赛,决定出前三名,这三名选出来之后再和刚才选出来的那批进行比赛,选出前三名,于是决出前四名:总场数为8+1+1+1=11场;