542.01 矩阵
给定一个由 0 和 1 组成的矩阵,找出每个元素到最近的 0 的距离。两个相邻元素间的距离为 1 。
示例 1:
输入:
0 0 0
0 1 0
0 0 0
输出:
0 0 0
0 1 0
0 0 0
示例 2:
输入:
0 0 0
0 1 0
1 1 1
输出:
0 0 0
0 1 0
1 2 1
思路:在一个图中,能从一个点出发求这种最短距离的方法很容易想到就是 BFS,BFS 的名称是广度优先遍历,即把周围这一圈搜索完成之后,再搜索下一圈,是慢慢扩大搜索范围的。
题目给出了多个1,要找出每个1到0的最近曼哈顿距离。由于1到0的距离和0到1的距离一样的,所以其实我们可以换个思维:找出每个0到1的距离。因此,题目可以抽象成:多个起始点的BFS。
class Solution:
def updateMatrix(self, matrix: List[List[int]]) -> List[List[int]]:
M, N = len(matrix), len(matrix[0])
queue = collections.deque()
visited = [[0] * N for _ in range(M)]
res = [[0] * N for _ in range(M)]
for i in range(M):
for j in range(N):
if matrix[i][j] == 0:
queue.append((i, j))
visited[i][j] = 1
dirs = [(0, 1), (0, -1), (1, 0), (-1, 0)]
step = 0
while queue:
size = len(queue)
for i in range(size):
x, y = queue.popleft()
if matrix[x][y] == 1:
res[x][y] = step
for dx, dy in dirs:
newx, newy = x + dx, y + dy
if newx < 0 or newx >= M or newy < 0 or newy >= N or visited[newx][newy] == 1:
continue
queue.append((newx, newy))
visited[newx][newy] = 1
step += 1
return res
200.岛屿数量
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。此外,你可以假设该网格的四条边均被水包围。
示例 1:
输入:
11110
11010
11000
00000
输出: 1
示例 2:
输入:
11000
11000
00100
00011
输出: 3
解释: 每座岛屿只能由水平和/或竖直方向上相邻的陆地连接而成。
思路1:核心思想依旧是 BFS,如果发现一个陆地,便对其进行 BFS,并将可由 BFS 访问到的点都置为已经访问状态,从而代表同属一个岛屿。
class Solution:
def numIslands(self, grid: List[List[str]]) -> int:
count = 0
for row in range(len(grid)):
for col in range(len(grid[0])):
if grid[row][col] == '1': # 发现陆地
count += 1 # 结果加1
grid[row][col] = '0' # 将其转为 ‘0’ 代表已经访问过
# 对发现的陆地进行扩张即执行 BFS,将与其相邻的陆地都标记为已访问
# 下面还是经典的 BFS 模板
land_positions = collections.deque()
land_positions.append([row, col])
while len(land_positions) > 0:
x, y = land_positions.popleft()
for new_x, new_y in [[x, y + 1], [x, y - 1], [x + 1, y], [x - 1, y]]: # 进行四个方向的扩张
# 判断有效性
if 0 <= new_x < len(grid) and 0 <= new_y < len(grid[0]) and grid[new_x][new_y] == '1':
grid[new_x][new_y] = '0' # 因为可由 BFS 访问到,代表同属一块岛,将其置 ‘0’ 代表已访问过
land_positions.append([new_x, new_y])
return count
思路2:DFS 类似感染思想,首先遍历整个grid,如果遇到1 则岛屿数量+1,随后,开始使用感染法,将周围的1都变成0,直到周围不是1后,继续开始遍历。如此便能得到有几个岛屿。
class Solution:
def numIslands(self, grid: List[List[str]]) -> int:
count = 0
for i in range(len(grid)):
for j in range(len(grid[0])):#遍历list
if grid[i][j] == '1':#开始有岛屿那么岛屿数量加1
count += 1
self.dfs(grid,i,j)#进入感染模式,把所有临近岛屿变为0
return count
def dfs(self,grid,i,j):#感染模式
if i<0 or j<0 or i>=len(grid) or j>=len(grid[0]) or grid[i][j] !='1':
return
else:
grid[i][j] = '0'
self.dfs(grid,i+1,j)
self.dfs(grid,i-1,j)
self.dfs(grid,i,j+1)
self.dfs(grid,i,j-1)
1162.地图分析
你现在手里有一份大小为 N x N 的「地图」(网格) grid,上面的每个「区域」(单元格)都用 0 和 1 标记好了。其中 0 代表海洋,1 代表陆地,请你找出一个海洋区域,这个海洋区域到离它最近的陆地区域的距离是最大的。我们这里说的距离是「曼哈顿距离」( Manhattan Distance):(x0, y0) 和 (x1, y1) 这两个区域之间的距离是 |x0 - x1| + |y0 - y1| 。如果我们的地图上只有陆地或者海洋,请返回 -1。
示例 1:

输入:[[1,0,1],[0,0,0],[1,0,1]]
输出:2
解释:
海洋区域 (1, 1) 和所有陆地区域之间的距离都达到最大,最大距离为 2。
示例 2:
输入:[[1,0,0],[0,0,0],[0,0,0]]
输出:4
解释:
海洋区域 (2, 2) 和所有陆地区域之间的距离都达到最大,最大距离为 4。
思路:由于这道题求解的是最远的距离,而距离我们可以使用BFS来做。
对于每一个海洋,我们都向四周扩展,寻找最近的陆地,每次扩展steps加1。
1.如果找到了陆地,我们返回steps。
2.我们的目标就是所有steps中的最大值。
3.实际上面算法有很多重复计算,如图中间绿色的区域,向外扩展的时候,如果其周边四个海洋的距离已经计算出来了,那么没必要扩展到陆地。实际上只需要扩展到周边的四个海洋格子就好了,其距离陆地的最近距离就是1 + 周边四个格子中到达陆地的最小距离。
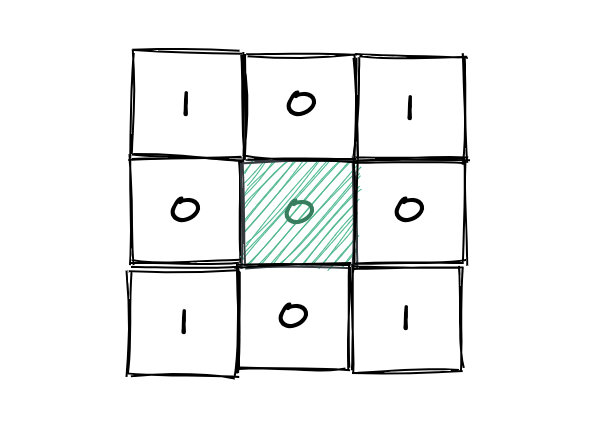
我们考虑优化。
1.将所有陆地加入队列,而不是海洋。
2.陆地不断扩展到海洋,每扩展一次就steps加1,直到无法扩展位置。
3.最终返回steps即可。

class Solution:
def maxDistance(self, grid: List[List[int]]) -> int:
n = len(grid)
steps = -1
queue = [(i, j) for i in range(n) for j in range(n) if grid[i][j] == 1]
if len(queue) == 0 or len(queue) == n ** 2: return steps
while len(queue) > 0:
for _ in range(len(queue)):
x, y = queue.pop(0)
for xi, yj in [(x + 1, y), (x - 1, y), (x, y + 1), (x, y - 1)]:
if xi >= 0 and xi < n and yj >= 0 and yj < n and grid[xi][yj] == 0:
queue.append((xi, yj))
grid[xi][yj] = -1
steps += 1
return steps
#由于没有early return,steps 其实会多算一次。 我们可以返回值减去1,也可以steps初始化为-1。这里我选择是steps初始化为-1
作者:fe-lucifer
链接:https://leetcode-cn.com/problems/as-far-from-land-as-possible/solution/python-tu-jie-chao-jian-dan-de-bfs1162-di-tu-fen-x/
来源:力扣(LeetCode)