
由上述推导可以看出,在使用MSE时,w、b的梯度均与sigmoid函数对z的偏导有关系,而sigmoid函数的偏导在自变量非常大或者非常小时,偏导数的值接近于零,这将导致w、b的梯度将不会变化,也就是出现所谓的梯度消失现象。而使用cross-entropy时,w、b的梯度就不会出现上述的情况。所以MSE不适用于分类问题。
2.交叉熵不适用于回归问题
当MSE和交叉熵同时应用到多分类场景下时,(标签的值为1时表示属于此分类,标签值为0时表示不属于此分类),MSE对于每一个输出的结果都非常看重,而交叉熵只对正确分类的结果看重。例如:在一个三分类模型中,模型的输出结果为(a,b,c),而真实的输出结果为(1,0,0),那么MSE与cross-entropy相对应的损失函数的值如下:
MSE:
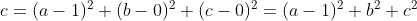
cross-entropy:
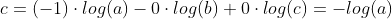
从上述的公式可以看出,交叉熵的损失函数只和分类正确的预测结果有关系,而MSE的损失函数还和错误的分类有关系,该分类函数除了让正确的分类尽量变大,还会让错误的分类变得平均,但实际在分类问题中这个调整是没有必要的。但是对于回归问题来说,这样的考虑就显得很重要了。所以,回归问题熵使用交叉上并不合适。